Sparsity-Constraint Optimization via Splicing Iteration

Sparsity-constraint optimization has wide applicability in signal processing, statistics, and machine learning. Existing fast algorithms must burdensomely tune parameters, such as the step size or the implementation of precise stop criteria, which may be challenging to determine in practice. To address this issue, we develop an algorithm named Sparsity-Constraint Optimization via sPlicing itEration (SCOPE) to optimize nonlinear differential objective functions with strong convexity and smoothness in low dimensional subspaces. Algorithmically, the SCOPE algorithm converges effectively without tuning parameters. Theoretically, SCOPE has a linear convergence rate and converges to a solution that recovers the true support set when it correctly specifies the sparsity. We also develop parallel theoretical results without restricted-isometry-property-type conditions. We apply SCOPE's versatility and power to solve sparse quadratic optimization, learn sparse classifiers, and recover sparse Markov networks for binary variables. The numerical results on these specific tasks reveal that SCOPE perfectly identifies the true support set with a 10--1000 speedup over the standard exact solver, confirming SCOPE's algorithmic and theoretical merits. Our open-source Python package skscope based on C++ implementation is publicly available on GitHub, reaching a ten-fold speedup on the competing convex relaxation methods implemented by the cvxpy library.

skscope: Fast Sparsity-Constrained Optimization in Python

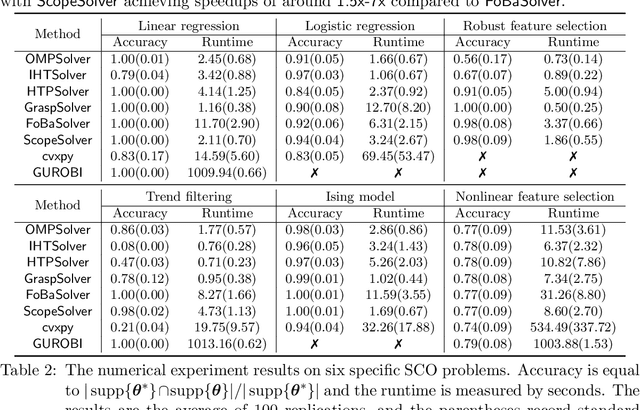
Applying iterative solvers on sparsity-constrained optimization (SCO) requires tedious mathematical deduction and careful programming/debugging that hinders these solvers' broad impact. In the paper, the library skscope is introduced to overcome such an obstacle. With skscope, users can solve the SCO by just programming the objective function. The convenience of skscope is demonstrated through two examples in the paper, where sparse linear regression and trend filtering are addressed with just four lines of code. More importantly, skscope's efficient implementation allows state-of-the-art solvers to quickly attain the sparse solution regardless of the high dimensionality of parameter space. Numerical experiments reveal the available solvers in skscope can achieve up to 80x speedup on the competing relaxation solutions obtained via the benchmarked convex solver. skscope is published on the Python Package Index (PyPI) and Conda, and its source code is available at: https://github.com/abess-team/skscope.

A Consistent and Scalable Algorithm for Best Subset Selection in Single Index Models

Analysis of high-dimensional data has led to increased interest in both single index models (SIMs) and best subset selection. SIMs provide an interpretable and flexible modeling framework for high-dimensional data, while best subset selection aims to find a sparse model from a large set of predictors. However, best subset selection in high-dimensional models is known to be computationally intractable. Existing methods tend to relax the selection, but do not yield the best subset solution. In this paper, we directly tackle the intractability by proposing the first provably scalable algorithm for best subset selection in high-dimensional SIMs. Our algorithmic solution enjoys the subset selection consistency and has the oracle property with a high probability. The algorithm comprises a generalized information criterion to determine the support size of the regression coefficients, eliminating the model selection tuning. Moreover, our method does not assume an error distribution or a specific link function and hence is flexible to apply. Extensive simulation results demonstrate that our method is not only computationally efficient but also able to exactly recover the best subset in various settings (e.g., linear regression, Poisson regression, heteroscedastic models).

Best-Subset Selection in Generalized Linear Models: A Fast and Consistent Algorithm via Splicing Technique

In high-dimensional generalized linear models, it is crucial to identify a sparse model that adequately accounts for response variation. Although the best subset section has been widely regarded as the Holy Grail of problems of this type, achieving either computational efficiency or statistical guarantees is challenging. In this article, we intend to surmount this obstacle by utilizing a fast algorithm to select the best subset with high certainty. We proposed and illustrated an algorithm for best subset recovery in regularity conditions. Under mild conditions, the computational complexity of our algorithm scales polynomially with sample size and dimension. In addition to demonstrating the statistical properties of our method, extensive numerical experiments reveal that it outperforms existing methods for variable selection and coefficient estimation. The runtime analysis shows that our implementation achieves approximately a fourfold speedup compared to popular variable selection toolkits like glmnet and ncvreg.

abess: A Fast Best Subset Selection Library in Python and R

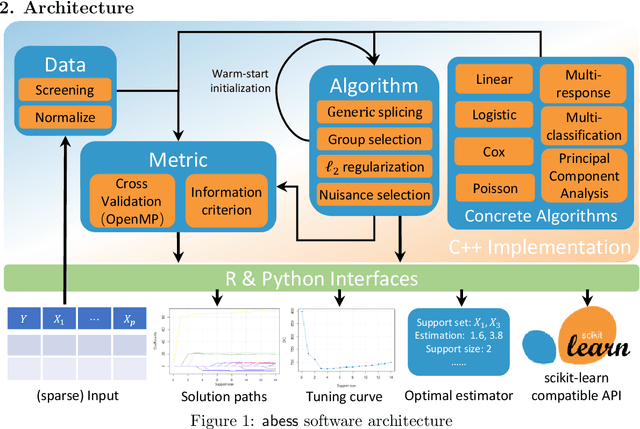
We introduce a new library named abess that implements a unified framework of best-subset selection for solving diverse machine learning problems, e.g., linear regression, classification, and principal component analysis. Particularly, the abess certifiably gets the optimal solution within polynomial times under the linear model. Our efficient implementation allows abess to attain the solution of best-subset selection problems as fast as or even 100x faster than existing competing variable (model) selection toolboxes. Furthermore, it supports common variants like best group subset selection and $\ell_2$ regularized best-subset selection. The core of the library is programmed in C++. For ease of use, a Python library is designed for conveniently integrating with scikit-learn, and it can be installed from the Python library Index. In addition, a user-friendly R library is available at the Comprehensive R Archive Network. The source code is available at: https://github.com/abess-team/abess.

Certifiably Polynomial Algorithm for Best Group Subset Selection

Best group subset selection aims to choose a small part of non-overlapping groups to achieve the best interpretability on the response variable. It is practically attractive for group variable selection; however, due to the computational intractability in high dimensionality setting, it doesn't catch enough attention. To fill the blank of efficient algorithms for best group subset selection, in this paper, we propose a group-splicing algorithm that iteratively detects effective groups and excludes the helpless ones. Moreover, coupled with a novel Bayesian group information criterion, an adaptive algorithm is developed to determine the true group subset size. It is certifiable that our algorithms enable identifying the optimal group subset in polynomial time under mild conditions. We demonstrate the efficiency and accuracy of our proposal by comparing state-of-the-art algorithms on both synthetic and real-world datasets.