Sparsity-Constraint Optimization via Splicing Iteration

Sparsity-constraint optimization has wide applicability in signal processing, statistics, and machine learning. Existing fast algorithms must burdensomely tune parameters, such as the step size or the implementation of precise stop criteria, which may be challenging to determine in practice. To address this issue, we develop an algorithm named Sparsity-Constraint Optimization via sPlicing itEration (SCOPE) to optimize nonlinear differential objective functions with strong convexity and smoothness in low dimensional subspaces. Algorithmically, the SCOPE algorithm converges effectively without tuning parameters. Theoretically, SCOPE has a linear convergence rate and converges to a solution that recovers the true support set when it correctly specifies the sparsity. We also develop parallel theoretical results without restricted-isometry-property-type conditions. We apply SCOPE's versatility and power to solve sparse quadratic optimization, learn sparse classifiers, and recover sparse Markov networks for binary variables. The numerical results on these specific tasks reveal that SCOPE perfectly identifies the true support set with a 10--1000 speedup over the standard exact solver, confirming SCOPE's algorithmic and theoretical merits. Our open-source Python package skscope based on C++ implementation is publicly available on GitHub, reaching a ten-fold speedup on the competing convex relaxation methods implemented by the cvxpy library.

skscope: Fast Sparsity-Constrained Optimization in Python

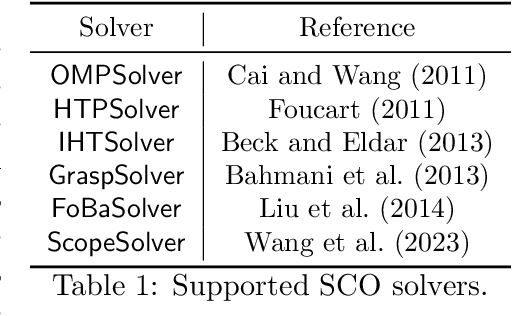
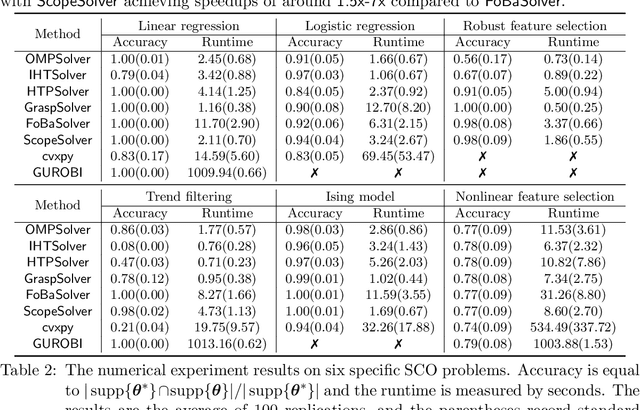
Applying iterative solvers on sparsity-constrained optimization (SCO) requires tedious mathematical deduction and careful programming/debugging that hinders these solvers' broad impact. In the paper, the library skscope is introduced to overcome such an obstacle. With skscope, users can solve the SCO by just programming the objective function. The convenience of skscope is demonstrated through two examples in the paper, where sparse linear regression and trend filtering are addressed with just four lines of code. More importantly, skscope's efficient implementation allows state-of-the-art solvers to quickly attain the sparse solution regardless of the high dimensionality of parameter space. Numerical experiments reveal the available solvers in skscope can achieve up to 80x speedup on the competing relaxation solutions obtained via the benchmarked convex solver. skscope is published on the Python Package Index (PyPI) and Conda, and its source code is available at: https://github.com/abess-team/skscope.