Maternal and Fetal Health Status Assessment by Using Machine Learning on Optical 3D Body Scans

Monitoring maternal and fetal health during pregnancy is crucial for preventing adverse outcomes. While tests such as ultrasound scans offer high accuracy, they can be costly and inconvenient. Telehealth and more accessible body shape information provide pregnant women with a convenient way to monitor their health. This study explores the potential of 3D body scan data, captured during the 18-24 gestational weeks, to predict adverse pregnancy outcomes and estimate clinical parameters. We developed a novel algorithm with two parallel streams which are used for extract body shape features: one for supervised learning to extract sequential abdominal circumference information, and another for unsupervised learning to extract global shape descriptors, alongside a branch for demographic data. Our results indicate that 3D body shape can assist in predicting preterm labor, gestational diabetes mellitus (GDM), gestational hypertension (GH), and in estimating fetal weight. Compared to other machine learning models, our algorithm achieved the best performance, with prediction accuracies exceeding 88% and fetal weight estimation accuracy of 76.74% within a 10% error margin, outperforming conventional anthropometric methods by 22.22%.

Liver Fat Quantification Network with Body Shape

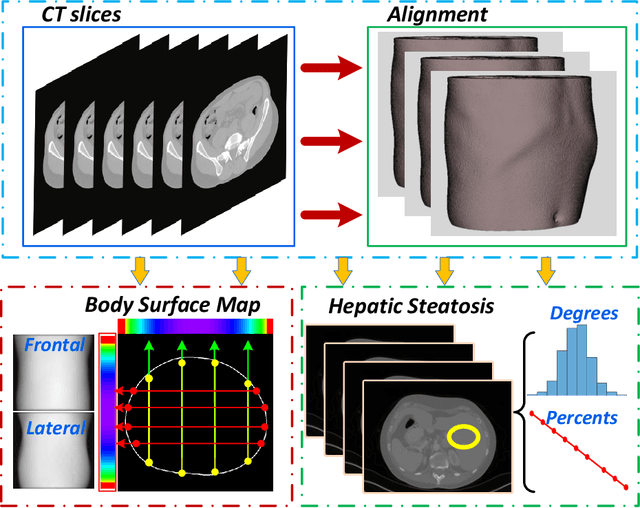
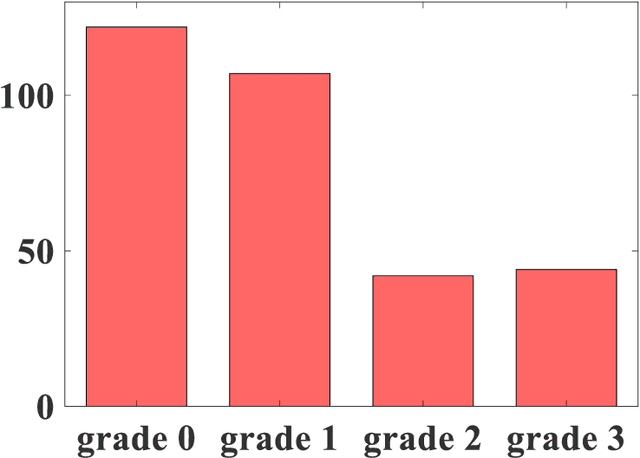
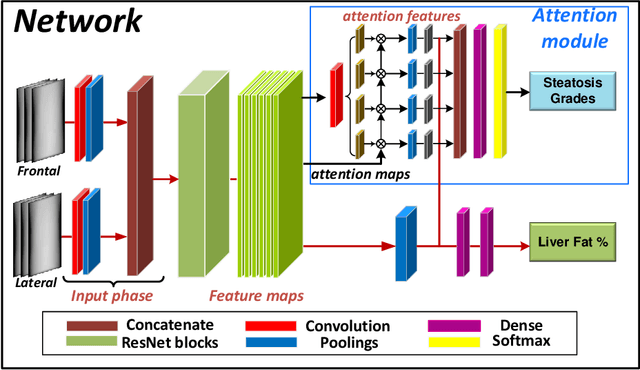
It is clinically important to detect liver fat content as it is related to cardiac complications and cardiovascular disease mortality. However, existing methods are associated with high cost and/or medical complications (e.g., liver biopsy, medical imaging technology) or only roughly estimate the grades of steatosis. In this paper, we propose a deep neural network to accurately estimate liver fat percentage using only body shapes. The proposed framework is composed of a flexible baseline regression network and a lightweight attention module. The attention module is trained to generate discriminative and diverse features, thus significantly improving performance. To validate our proposed method, we perform extensive tests on medical datasets. The experimental results validate our method and prove the efficacy of designing neural networks to predict liver fat using only body shape. Since body shapes can be acquired using inexpensive and readily available optical scanners, the proposed method promised to make accurate assessment of hepatic steatosis more accessible.

skscope: Fast Sparsity-Constrained Optimization in Python

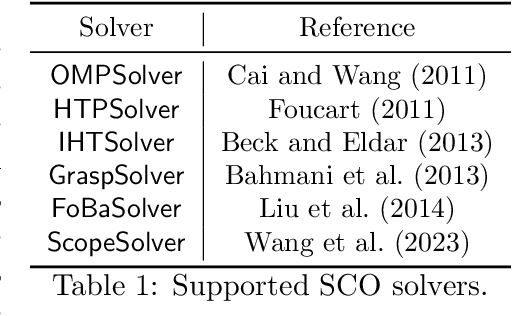
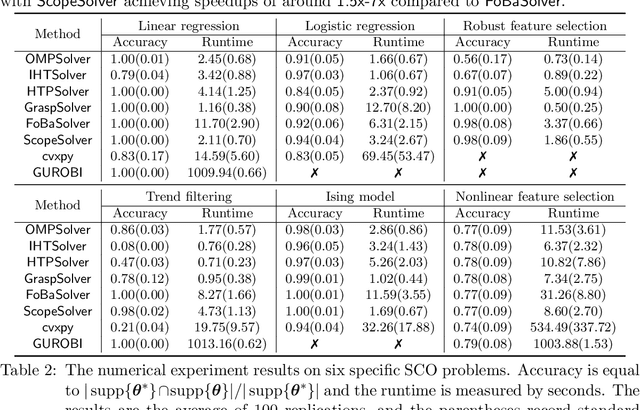
Applying iterative solvers on sparsity-constrained optimization (SCO) requires tedious mathematical deduction and careful programming/debugging that hinders these solvers' broad impact. In the paper, the library skscope is introduced to overcome such an obstacle. With skscope, users can solve the SCO by just programming the objective function. The convenience of skscope is demonstrated through two examples in the paper, where sparse linear regression and trend filtering are addressed with just four lines of code. More importantly, skscope's efficient implementation allows state-of-the-art solvers to quickly attain the sparse solution regardless of the high dimensionality of parameter space. Numerical experiments reveal the available solvers in skscope can achieve up to 80x speedup on the competing relaxation solutions obtained via the benchmarked convex solver. skscope is published on the Python Package Index (PyPI) and Conda, and its source code is available at: https://github.com/abess-team/skscope.

Off-Policy Evaluation for Episodic Partially Observable Markov Decision Processes under Non-Parametric Models

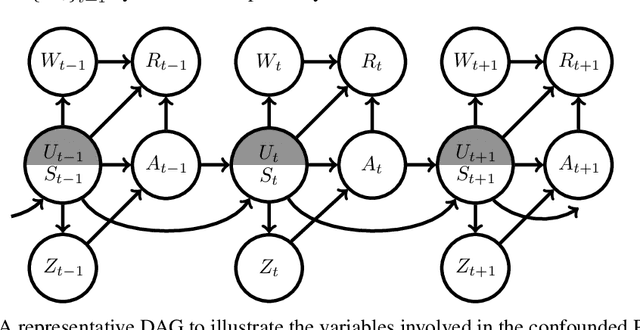
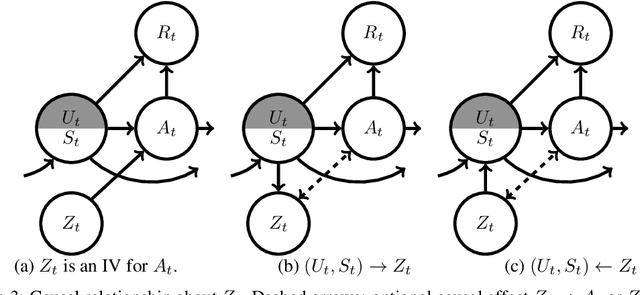
We study the problem of off-policy evaluation (OPE) for episodic Partially Observable Markov Decision Processes (POMDPs) with continuous states. Motivated by the recently proposed proximal causal inference framework, we develop a non-parametric identification result for estimating the policy value via a sequence of so-called V-bridge functions with the help of time-dependent proxy variables. We then develop a fitted-Q-evaluation-type algorithm to estimate V-bridge functions recursively, where a non-parametric instrumental variable (NPIV) problem is solved at each step. By analyzing this challenging sequential NPIV problem, we establish the finite-sample error bounds for estimating the V-bridge functions and accordingly that for evaluating the policy value, in terms of the sample size, length of horizon and so-called (local) measure of ill-posedness at each step. To the best of our knowledge, this is the first finite-sample error bound for OPE in POMDPs under non-parametric models.

Proximal Learning for Individualized Treatment Regimes Under Unmeasured Confounding

Data-driven individualized decision making has recently received increasing research interests. Most existing methods rely on the assumption of no unmeasured confounding, which unfortunately cannot be ensured in practice especially in observational studies. Motivated by the recent proposed proximal causal inference, we develop several proximal learning approaches to estimating optimal individualized treatment regimes (ITRs) in the presence of unmeasured confounding. In particular, we establish several identification results for different classes of ITRs, exhibiting the trade-off between the risk of making untestable assumptions and the value function improvement in decision making. Based on these results, we propose several classification-based approaches to finding a variety of restricted in-class optimal ITRs and develop their theoretical properties. The appealing numerical performance of our proposed methods is demonstrated via an extensive simulation study and one real data application.