How to Solve Contextual Goal-Oriented Problems with Offline Datasets?

We present a novel method, Contextual goal-Oriented Data Augmentation (CODA), which uses commonly available unlabeled trajectories and context-goal pairs to solve Contextual Goal-Oriented (CGO) problems. By carefully constructing an action-augmented MDP that is equivalent to the original MDP, CODA creates a fully labeled transition dataset under training contexts without additional approximation error. We conduct a novel theoretical analysis to demonstrate CODA's capability to solve CGO problems in the offline data setup. Empirical results also showcase the effectiveness of CODA, which outperforms other baseline methods across various context-goal relationships of CGO problem. This approach offers a promising direction to solving CGO problems using offline datasets.

Steering LLMs Towards Unbiased Responses: A Causality-Guided Debiasing Framework

Large language models (LLMs) can easily generate biased and discriminative responses. As LLMs tap into consequential decision-making (e.g., hiring and healthcare), it is of crucial importance to develop strategies to mitigate these biases. This paper focuses on social bias, tackling the association between demographic information and LLM outputs. We propose a causality-guided debiasing framework that utilizes causal understandings of (1) the data-generating process of the training corpus fed to LLMs, and (2) the internal reasoning process of LLM inference, to guide the design of prompts for debiasing LLM outputs through selection mechanisms. Our framework unifies existing de-biasing prompting approaches such as inhibitive instructions and in-context contrastive examples, and sheds light on new ways of debiasing by encouraging bias-free reasoning. Our strong empirical performance on real-world datasets demonstrates that our framework provides principled guidelines on debiasing LLM outputs even with only the black-box access.

VQ-GNN: A Universal Framework to Scale up Graph Neural Networks using Vector Quantization

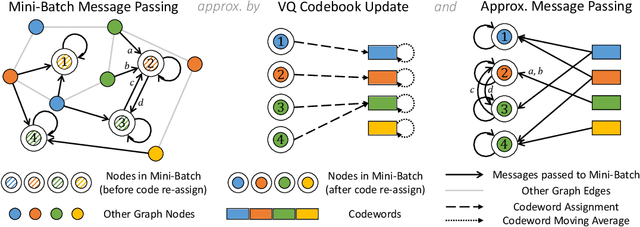
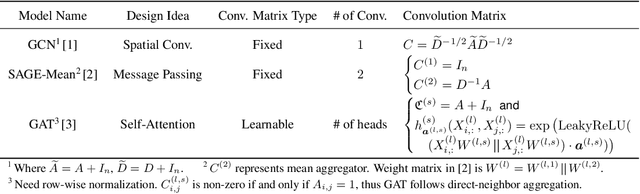
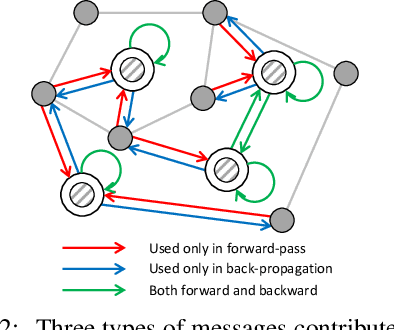
Most state-of-the-art Graph Neural Networks (GNNs) can be defined as a form of graph convolution which can be realized by message passing between direct neighbors or beyond. To scale such GNNs to large graphs, various neighbor-, layer-, or subgraph-sampling techniques are proposed to alleviate the "neighbor explosion" problem by considering only a small subset of messages passed to the nodes in a mini-batch. However, sampling-based methods are difficult to apply to GNNs that utilize many-hops-away or global context each layer, show unstable performance for different tasks and datasets, and do not speed up model inference. We propose a principled and fundamentally different approach, VQ-GNN, a universal framework to scale up any convolution-based GNNs using Vector Quantization (VQ) without compromising the performance. In contrast to sampling-based techniques, our approach can effectively preserve all the messages passed to a mini-batch of nodes by learning and updating a small number of quantized reference vectors of global node representations, using VQ within each GNN layer. Our framework avoids the "neighbor explosion" problem of GNNs using quantized representations combined with a low-rank version of the graph convolution matrix. We show that such a compact low-rank version of the gigantic convolution matrix is sufficient both theoretically and experimentally. In company with VQ, we design a novel approximated message passing algorithm and a nontrivial back-propagation rule for our framework. Experiments on various types of GNN backbones demonstrate the scalability and competitive performance of our framework on large-graph node classification and link prediction benchmarks.

Noisy Labels Can Induce Good Representations

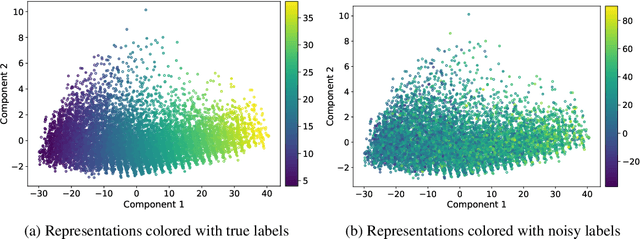
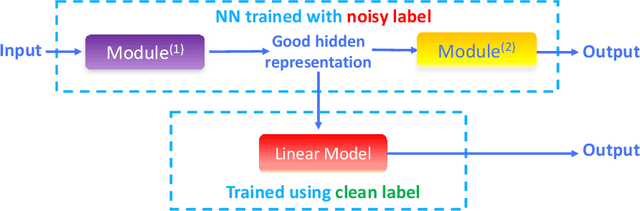
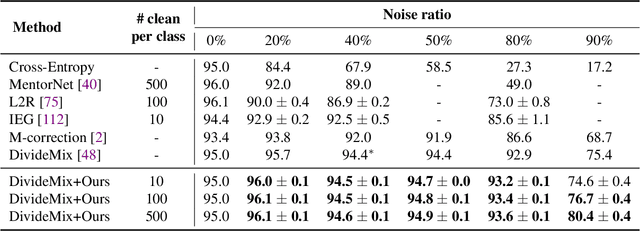
The current success of deep learning depends on large-scale labeled datasets. In practice, high-quality annotations are expensive to collect, but noisy annotations are more affordable. Previous works report mixed empirical results when training with noisy labels: neural networks can easily memorize random labels, but they can also generalize from noisy labels. To explain this puzzle, we study how architecture affects learning with noisy labels. We observe that if an architecture "suits" the task, training with noisy labels can induce useful hidden representations, even when the model generalizes poorly; i.e., the last few layers of the model are more negatively affected by noisy labels. This finding leads to a simple method to improve models trained on noisy labels: replacing the final dense layers with a linear model, whose weights are learned from a small set of clean data. We empirically validate our findings across three architectures (Convolutional Neural Networks, Graph Neural Networks, and Multi-Layer Perceptrons) and two domains (graph algorithmic tasks and image classification). Furthermore, we achieve state-of-the-art results on image classification benchmarks by combining our method with existing approaches on noisy label training.

How Neural Networks Extrapolate: From Feedforward to Graph Neural Networks

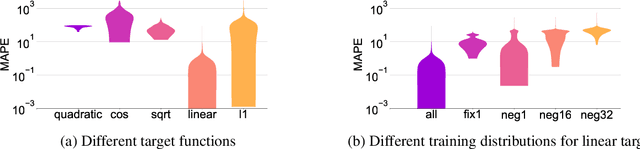
We study how neural networks trained by gradient descent extrapolate, i.e., what they learn outside the support of the training distribution. Previous works report mixed empirical results when extrapolating with neural networks: while multilayer perceptrons (MLPs) do not extrapolate well in certain simple tasks, Graph Neural Network (GNN), a structured network with MLP modules, has shown some success in more complex tasks. Working towards a theoretical explanation, we identify conditions under which MLPs and GNNs extrapolate well. First, we quantify the observation that ReLU MLPs quickly converge to linear functions along any direction from the origin, which implies that ReLU MLPs do not extrapolate most non-linear functions. But, they can provably learn a linear target function when the training distribution is sufficiently "diverse". Second, in connection to analyzing successes and limitations of GNNs, these results suggest a hypothesis for which we provide theoretical and empirical evidence: the success of GNNs in extrapolating algorithmic tasks to new data (e.g., larger graphs or edge weights) relies on encoding task-specific non-linearities in the architecture or features.

Understanding Generalization in Deep Learning via Tensor Methods

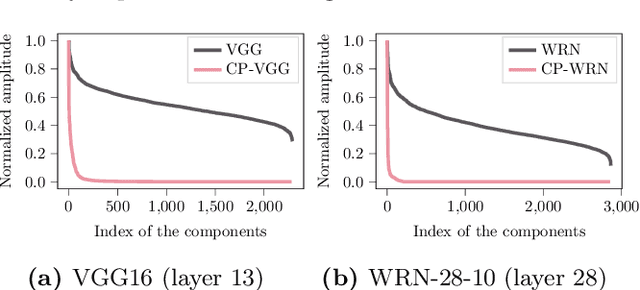
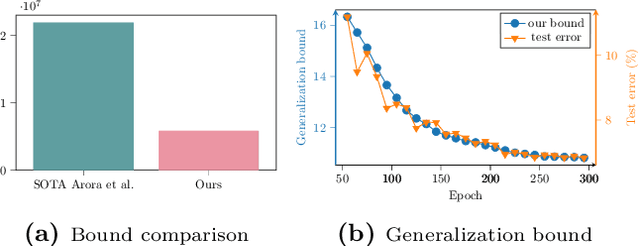
Deep neural networks generalize well on unseen data though the number of parameters often far exceeds the number of training examples. Recently proposed complexity measures have provided insights to understanding the generalizability in neural networks from perspectives of PAC-Bayes, robustness, overparametrization, compression and so on. In this work, we advance the understanding of the relations between the network's architecture and its generalizability from the compression perspective. Using tensor analysis, we propose a series of intuitive, data-dependent and easily-measurable properties that tightly characterize the compressibility and generalizability of neural networks; thus, in practice, our generalization bound outperforms the previous compression-based ones, especially for neural networks using tensors as their weight kernels (e.g. CNNs). Moreover, these intuitive measurements provide further insights into designing neural network architectures with properties favorable for better/guaranteed generalizability. Our experimental results demonstrate that through the proposed measurable properties, our generalization error bound matches the trend of the test error well. Our theoretical analysis further provides justifications for the empirical success and limitations of some widely-used tensor-based compression approaches. We also discover the improvements to the compressibility and robustness of current neural networks when incorporating tensor operations via our proposed layer-wise structure.

What Can Neural Networks Reason About?

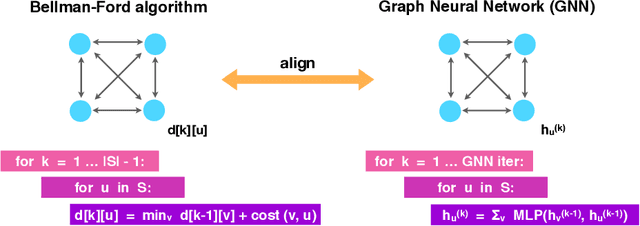
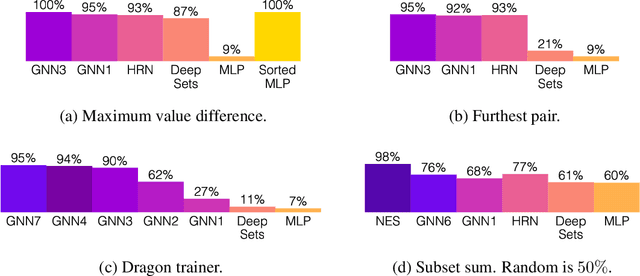
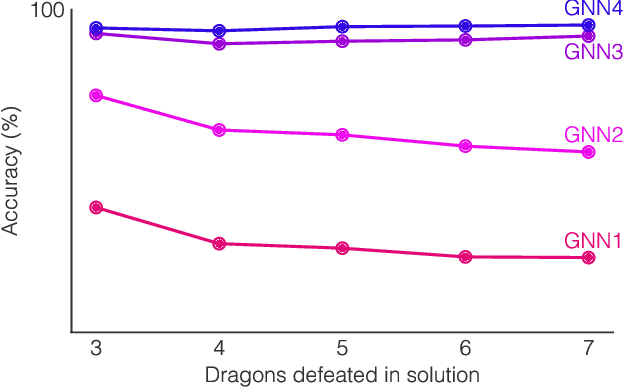
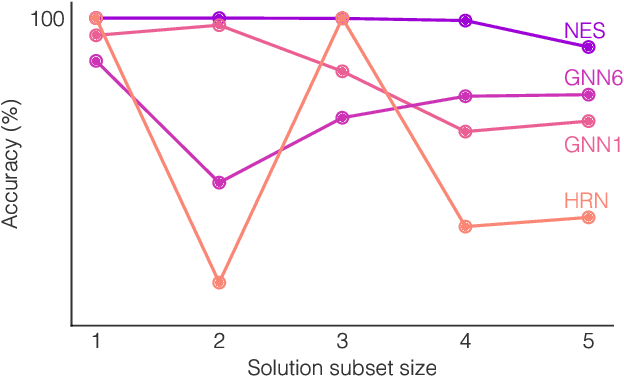
Neural networks have successfully been applied to solving reasoning tasks, ranging from learning simple concepts like "close to", to intricate questions whose reasoning procedures resemble algorithms. Empirically, not all network structures work equally well for reasoning. For example, Graph Neural Networks have achieved impressive empirical results, while less structured neural networks may fail to learn to reason. Theoretically, there is currently limited understanding of the interplay between reasoning tasks and network learning. In this paper, we develop a framework to characterize which tasks a neural network can learn well, by studying how well its structure aligns with the algorithmic structure of the relevant reasoning procedure. This suggests that Graph Neural Networks can learn dynamic programming, a powerful algorithmic strategy that solves a broad class of reasoning problems, such as relational question answering, sorting, intuitive physics, and shortest paths. Our perspective also implies strategies to design neural architectures for complex reasoning. On several abstract reasoning tasks, we see empirically that our theory aligns well with practice.

Tensorized Spectrum Preserving Compression for Neural Networks

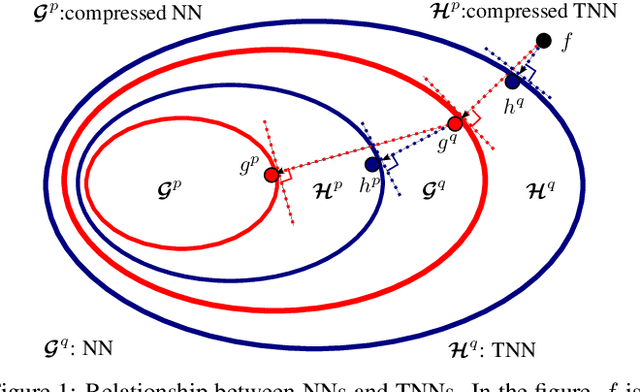
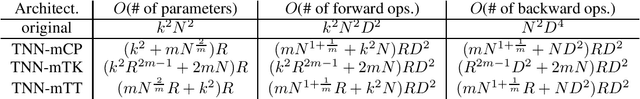
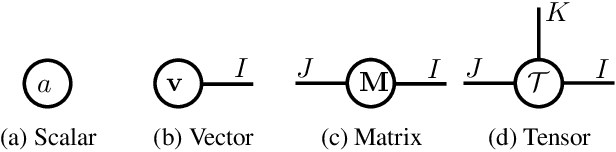
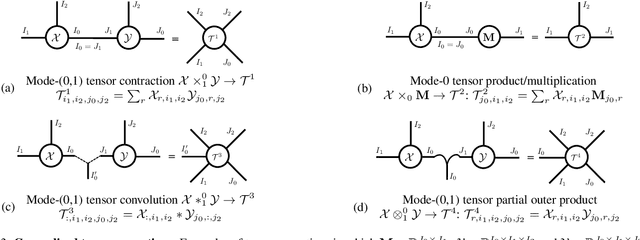
Modern neural networks can have tens of millions of parameters, and are often ill-suited for smartphones or IoT devices. In this paper, we describe an efficient mechanism for compressing large networks by {\em tensorizing\/} network layers: i.e. mapping layers on to high-order matrices, for which we introduce new tensor decomposition methods. Compared to previous compression methods, some of which use tensor decomposition, our techniques preserve more of the networks invariance structure. Coupled with a new data reconstruction-based learning method, we show that tensorized compression outperforms existing techniques for both convolutional and fully-connected layers on state-of-the art networks.