What Can Neural Networks Reason About?

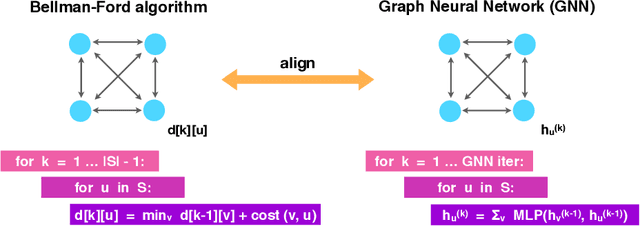
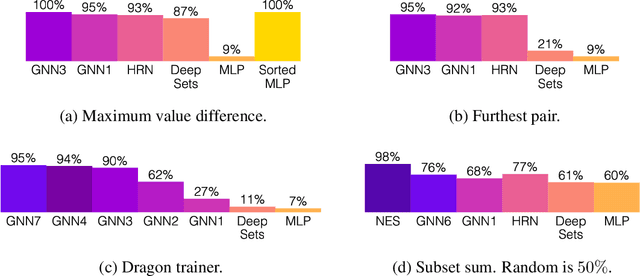
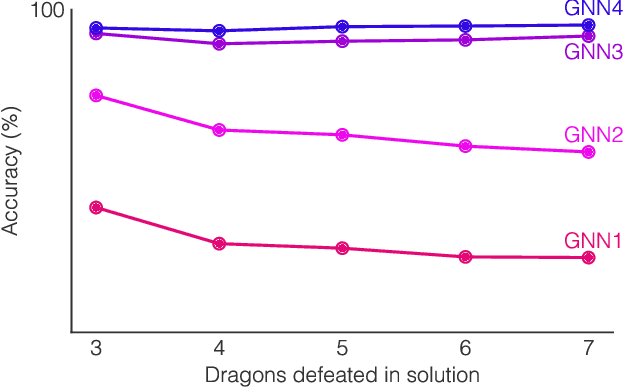
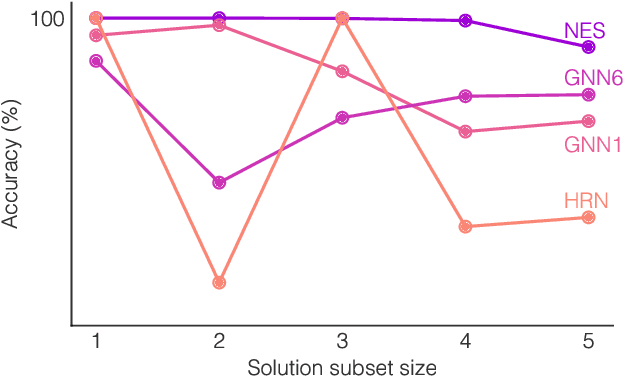
Neural networks have successfully been applied to solving reasoning tasks, ranging from learning simple concepts like "close to", to intricate questions whose reasoning procedures resemble algorithms. Empirically, not all network structures work equally well for reasoning. For example, Graph Neural Networks have achieved impressive empirical results, while less structured neural networks may fail to learn to reason. Theoretically, there is currently limited understanding of the interplay between reasoning tasks and network learning. In this paper, we develop a framework to characterize which tasks a neural network can learn well, by studying how well its structure aligns with the algorithmic structure of the relevant reasoning procedure. This suggests that Graph Neural Networks can learn dynamic programming, a powerful algorithmic strategy that solves a broad class of reasoning problems, such as relational question answering, sorting, intuitive physics, and shortest paths. Our perspective also implies strategies to design neural architectures for complex reasoning. On several abstract reasoning tasks, we see empirically that our theory aligns well with practice.