Obtaining Optimal Spiking Neural Network in Sequence Learning via CRNN-SNN Conversion

Spiking neural networks (SNNs) are becoming a promising alternative to conventional artificial neural networks (ANNs) due to their rich neural dynamics and the implementation of energy-efficient neuromorphic chips. However, the non-differential binary communication mechanism makes SNN hard to converge to an ANN-level accuracy. When SNN encounters sequence learning, the situation becomes worse due to the difficulties in modeling long-range dependencies. To overcome these difficulties, researchers developed variants of LIF neurons and different surrogate gradients but still failed to obtain good results when the sequence became longer (e.g., $>$500). Unlike them, we obtain an optimal SNN in sequence learning by directly mapping parameters from a quantized CRNN. We design two sub-pipelines to support the end-to-end conversion of different structures in neural networks, which is called CNN-Morph (CNN $\rightarrow$ QCNN $\rightarrow$ BIFSNN) and RNN-Morph (RNN $\rightarrow$ QRNN $\rightarrow$ RBIFSNN). Using conversion pipelines and the s-analog encoding method, the conversion error of our framework is zero. Furthermore, we give the theoretical and experimental demonstration of the lossless CRNN-SNN conversion. Our results show the effectiveness of our method over short and long timescales tasks compared with the state-of-the-art learning- and conversion-based methods. We reach the highest accuracy of 99.16% (0.46 $\uparrow$) on S-MNIST, 94.95% (3.95 $\uparrow$) on PS-MNIST (sequence length of 784) respectively, and the lowest loss of 0.057 (0.013 $\downarrow$) within 8 time-steps in collision avoidance dataset.

conv_einsum: A Framework for Representation and Fast Evaluation of Multilinear Operations in Convolutional Tensorial Neural Networks

Modern ConvNets continue to achieve state-of-the-art results over a vast array of vision and image classification tasks, but at the cost of increasing parameters. One strategy for compactifying a network without sacrificing much expressive power is to reshape it into a tensorial neural network (TNN), which is a higher-order tensorization of its layers, followed by a factorization, such as a CP-decomposition, which strips a weight down to its critical basis components. Passes through TNNs can be represented as sequences of multilinear operations (MLOs), where the evaluation path can greatly affect the number of floating point operations (FLOPs) incurred. While functions such as the popular einsum can evaluate simple MLOs such as contractions, existing implementations cannot process multi-way convolutions, resulting in scant assessments of how optimal evaluation paths through tensorized convolutional layers can improve training speed. In this paper, we develop a unifying framework for representing tensorial convolution layers as einsum-like strings and a meta-algorithm conv_einsum which is able to evaluate these strings in a FLOPs-minimizing manner. Comprehensive experiments, using our open-source implementation, over a wide range of models, tensor decompositions, and diverse tasks, demonstrate that conv_einsum significantly increases both computational and memory-efficiency of convolutional TNNs.

LEMON: Lossless model expansion

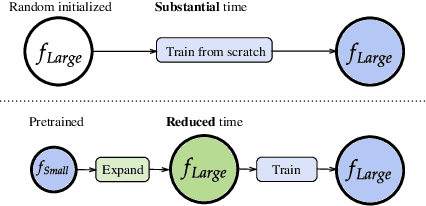
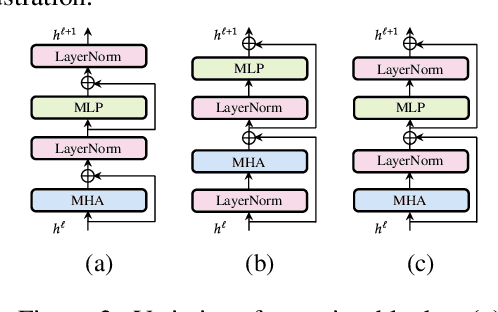
Scaling of deep neural networks, especially Transformers, is pivotal for their surging performance and has further led to the emergence of sophisticated reasoning capabilities in foundation models. Such scaling generally requires training large models from scratch with random initialization, failing to leverage the knowledge acquired by their smaller counterparts, which are already resource-intensive to obtain. To tackle this inefficiency, we present $\textbf{L}$ossl$\textbf{E}$ss $\textbf{MO}$del Expansio$\textbf{N}$ (LEMON), a recipe to initialize scaled models using the weights of their smaller but pre-trained counterparts. This is followed by model training with an optimized learning rate scheduler tailored explicitly for the scaled models, substantially reducing the training time compared to training from scratch. Notably, LEMON is versatile, ensuring compatibility with various network structures, including models like Vision Transformers and BERT. Our empirical results demonstrate that LEMON reduces computational costs by 56.7% for Vision Transformers and 33.2% for BERT when compared to training from scratch.

Reviving Shift Equivariance in Vision Transformers

Shift equivariance is a fundamental principle that governs how we perceive the world - our recognition of an object remains invariant with respect to shifts. Transformers have gained immense popularity due to their effectiveness in both language and vision tasks. While the self-attention operator in vision transformers (ViT) is permutation-equivariant and thus shift-equivariant, patch embedding, positional encoding, and subsampled attention in ViT variants can disrupt this property, resulting in inconsistent predictions even under small shift perturbations. Although there is a growing trend in incorporating the inductive bias of convolutional neural networks (CNNs) into vision transformers, it does not fully address the issue. We propose an adaptive polyphase anchoring algorithm that can be seamlessly integrated into vision transformer models to ensure shift-equivariance in patch embedding and subsampled attention modules, such as window attention and global subsampled attention. Furthermore, we utilize depth-wise convolution to encode positional information. Our algorithms enable ViT, and its variants such as Twins to achieve 100% consistency with respect to input shift, demonstrate robustness to cropping, flipping, and affine transformations, and maintain consistent predictions even when the original models lose 20 percentage points on average when shifted by just a few pixels with Twins' accuracy dropping from 80.57% to 62.40%.

Adversarial Auto-Augment with Label Preservation: A Representation Learning Principle Guided Approach

Data augmentation is a critical contributing factor to the success of deep learning but heavily relies on prior domain knowledge which is not always available. Recent works on automatic data augmentation learn a policy to form a sequence of augmentation operations, which are still pre-defined and restricted to limited options. In this paper, we show that a prior-free autonomous data augmentation's objective can be derived from a representation learning principle that aims to preserve the minimum sufficient information of the labels. Given an example, the objective aims at creating a distant "hard positive example" as the augmentation, while still preserving the original label. We then propose a practical surrogate to the objective that can be optimized efficiently and integrated seamlessly into existing methods for a broad class of machine learning tasks, e.g., supervised, semi-supervised, and noisy-label learning. Unlike previous works, our method does not require training an extra generative model but instead leverages the intermediate layer representations of the end-task model for generating data augmentations. In experiments, we show that our method consistently brings non-trivial improvements to the three aforementioned learning tasks from both efficiency and final performance, either or not combined with strong pre-defined augmentations, e.g., on medical images when domain knowledge is unavailable and the existing augmentation techniques perform poorly. Code is available at: https://github.com/kai-wen-yang/LPA3}{https://github.com/kai-wen-yang/LPA3.

Certified Defense via Latent Space Randomized Smoothing with Orthogonal Encoders

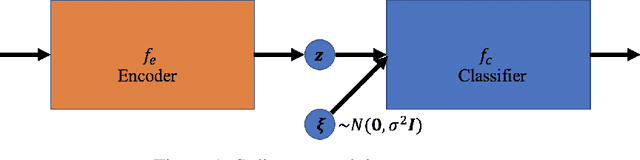
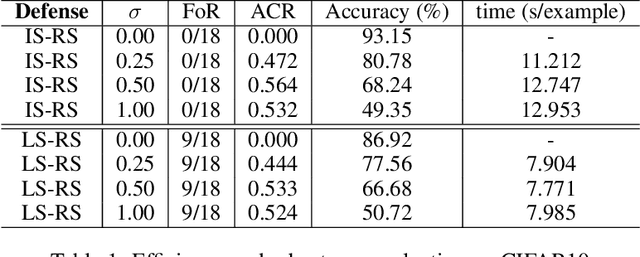
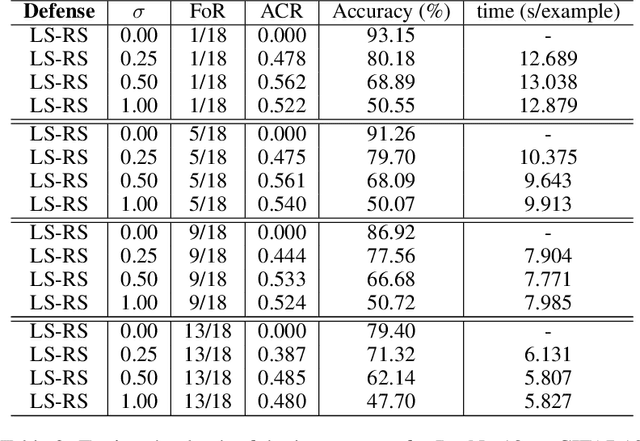
Randomized Smoothing (RS), being one of few provable defenses, has been showing great effectiveness and scalability in terms of defending against $\ell_2$-norm adversarial perturbations. However, the cost of MC sampling needed in RS for evaluation is high and computationally expensive. To address this issue, we investigate the possibility of performing randomized smoothing and establishing the robust certification in the latent space of a network, so that the overall dimensionality of tensors involved in computation could be drastically reduced. To this end, we propose Latent Space Randomized Smoothing. Another important aspect is that we use orthogonal modules, whose Lipschitz property is known for free by design, to propagate the certified radius estimated in the latent space back to the input space, providing valid certifiable regions for the test samples in the input space. Experiments on CIFAR10 and ImageNet show that our method achieves competitive certified robustness but with a significant improvement of efficiency during the test phase.

Scaling-up Diverse Orthogonal Convolutional Networks with a Paraunitary Framework

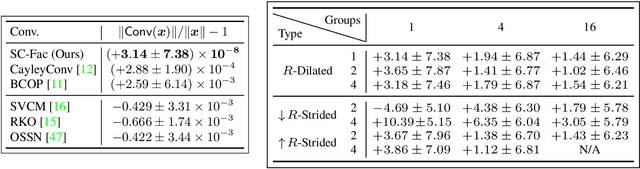
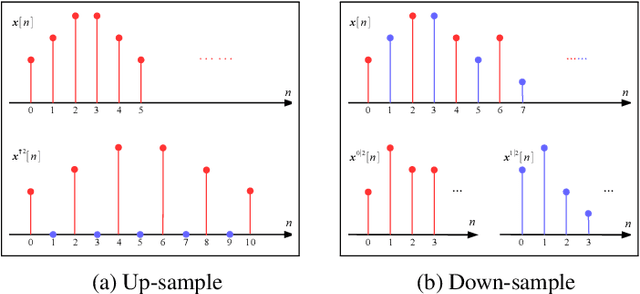
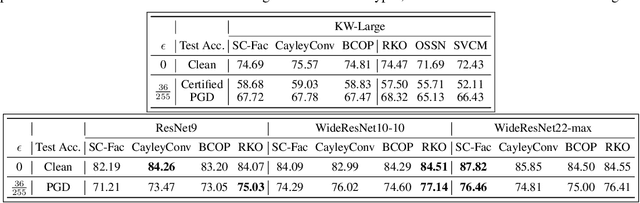
Enforcing orthogonality in neural networks is an antidote for gradient vanishing/exploding problems, sensitivity by adversarial perturbation, and bounding generalization errors. However, many previous approaches are heuristic, and the orthogonality of convolutional layers is not systematically studied: some of these designs are not exactly orthogonal, while others only consider standard convolutional layers and propose specific classes of their realizations. To address this problem, we propose a theoretical framework for orthogonal convolutional layers, which establishes the equivalence between various orthogonal convolutional layers in the spatial domain and the paraunitary systems in the spectral domain. Since there exists a complete spectral factorization of paraunitary systems, any orthogonal convolution layer can be parameterized as convolutions of spatial filters. Our framework endows high expressive power to various convolutional layers while maintaining their exact orthogonality. Furthermore, our layers are memory and computationally efficient for deep networks compared to previous designs. Our versatile framework, for the first time, enables the study of architecture designs for deep orthogonal networks, such as choices of skip connection, initialization, stride, and dilation. Consequently, we scale up orthogonal networks to deep architectures, including ResNet, WideResNet, and ShuffleNet, substantially increasing the performance over the traditional shallow orthogonal networks.

Convolutional Tensor-Train LSTM for Spatio-temporal Learning

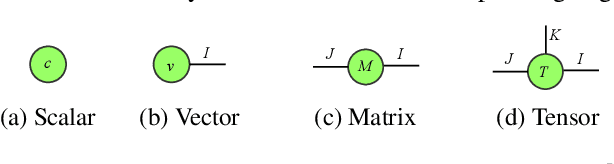
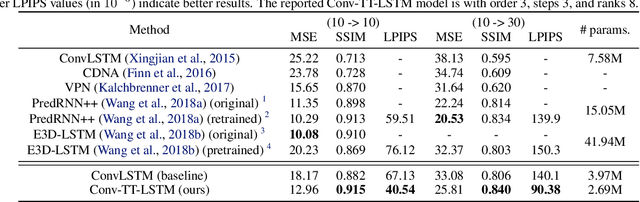
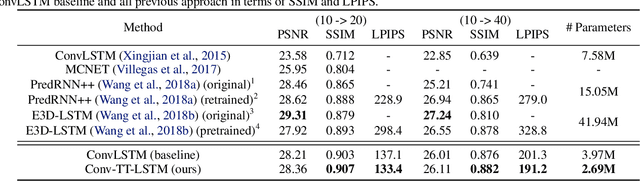
Higher-order Recurrent Neural Networks (RNNs) are effective for long-term forecasting since such architectures can model higher-order correlations and long-term dynamics more effectively. However, higher-order models are expensive and require exponentially more parameters and operations compared with their first-order counterparts. This problem is particularly pronounced in multidimensional data such as videos. To address this issue, we propose Convolutional Tensor-Train Decomposition (CTTD), a novel tensor decomposition with convolutional operations. With CTTD, we construct Convolutional Tensor-Train LSTM (Conv-TT-LSTM) to capture higher-order space-time correlations in videos. We demonstrate that the proposed model outperforms the conventional (first-order) Convolutional LSTM (ConvLSTM) as well as the state-of-the-art ConvLSTM-based approaches in pixel-level video prediction tasks on Moving-MNIST and KTH action datasets, but with much fewer parameters.

ARMA Nets: Expanding Receptive Field for Dense Prediction

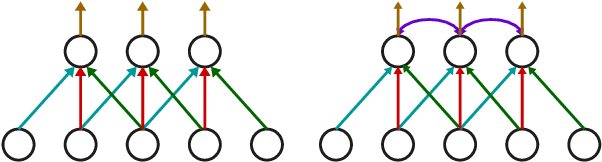
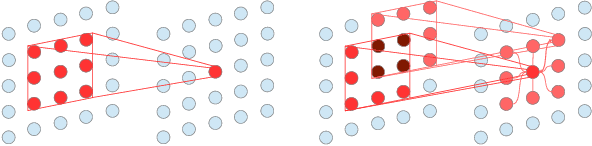
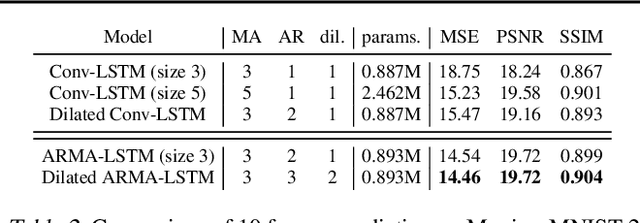
Global information is essential for dense prediction problems, whose goal is to compute a discrete or continuous label for each pixel in the images. Traditional convolutional layers in neural networks, originally designed for image classification, are restrictive in these problems since their receptive fields are limited by the filter size. In this work, we propose autoregressive moving-average (ARMA) layer, a novel module in neural networks to allow explicit dependencies of output neurons, which significantly expands the receptive field with minimal extra parameters. We show experimentally that the effective receptive field of neural networks with ARMA layers expands as autoregressive coefficients become larger. In addition, we demonstrate that neural networks with ARMA layers substantially improve the performance of challenging pixel-level video prediction tasks as our model enlarges the effective receptive field.

Understanding Generalization in Deep Learning via Tensor Methods

Deep neural networks generalize well on unseen data though the number of parameters often far exceeds the number of training examples. Recently proposed complexity measures have provided insights to understanding the generalizability in neural networks from perspectives of PAC-Bayes, robustness, overparametrization, compression and so on. In this work, we advance the understanding of the relations between the network's architecture and its generalizability from the compression perspective. Using tensor analysis, we propose a series of intuitive, data-dependent and easily-measurable properties that tightly characterize the compressibility and generalizability of neural networks; thus, in practice, our generalization bound outperforms the previous compression-based ones, especially for neural networks using tensors as their weight kernels (e.g. CNNs). Moreover, these intuitive measurements provide further insights into designing neural network architectures with properties favorable for better/guaranteed generalizability. Our experimental results demonstrate that through the proposed measurable properties, our generalization error bound matches the trend of the test error well. Our theoretical analysis further provides justifications for the empirical success and limitations of some widely-used tensor-based compression approaches. We also discover the improvements to the compressibility and robustness of current neural networks when incorporating tensor operations via our proposed layer-wise structure.