Certified Defense via Latent Space Randomized Smoothing with Orthogonal Encoders

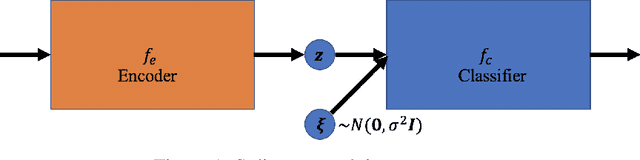
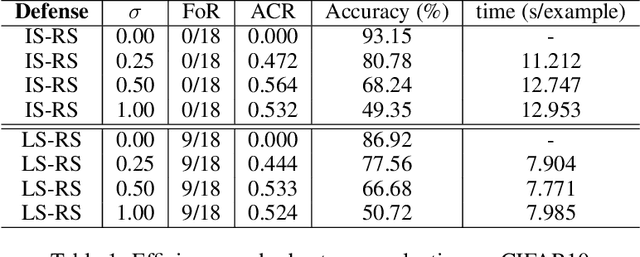
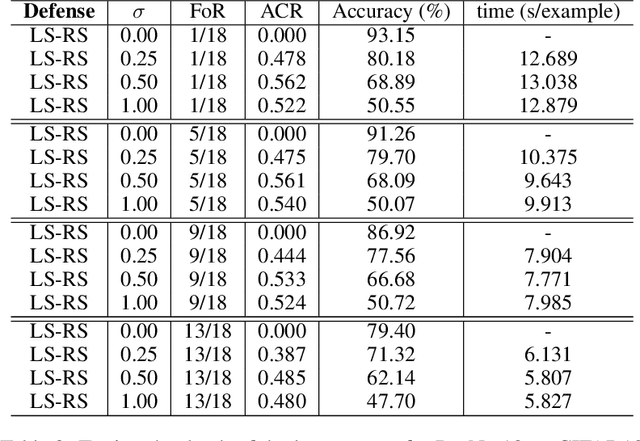
Randomized Smoothing (RS), being one of few provable defenses, has been showing great effectiveness and scalability in terms of defending against $\ell_2$-norm adversarial perturbations. However, the cost of MC sampling needed in RS for evaluation is high and computationally expensive. To address this issue, we investigate the possibility of performing randomized smoothing and establishing the robust certification in the latent space of a network, so that the overall dimensionality of tensors involved in computation could be drastically reduced. To this end, we propose Latent Space Randomized Smoothing. Another important aspect is that we use orthogonal modules, whose Lipschitz property is known for free by design, to propagate the certified radius estimated in the latent space back to the input space, providing valid certifiable regions for the test samples in the input space. Experiments on CIFAR10 and ImageNet show that our method achieves competitive certified robustness but with a significant improvement of efficiency during the test phase.