Reviving Shift Equivariance in Vision Transformers

Shift equivariance is a fundamental principle that governs how we perceive the world - our recognition of an object remains invariant with respect to shifts. Transformers have gained immense popularity due to their effectiveness in both language and vision tasks. While the self-attention operator in vision transformers (ViT) is permutation-equivariant and thus shift-equivariant, patch embedding, positional encoding, and subsampled attention in ViT variants can disrupt this property, resulting in inconsistent predictions even under small shift perturbations. Although there is a growing trend in incorporating the inductive bias of convolutional neural networks (CNNs) into vision transformers, it does not fully address the issue. We propose an adaptive polyphase anchoring algorithm that can be seamlessly integrated into vision transformer models to ensure shift-equivariance in patch embedding and subsampled attention modules, such as window attention and global subsampled attention. Furthermore, we utilize depth-wise convolution to encode positional information. Our algorithms enable ViT, and its variants such as Twins to achieve 100% consistency with respect to input shift, demonstrate robustness to cropping, flipping, and affine transformations, and maintain consistent predictions even when the original models lose 20 percentage points on average when shifted by just a few pixels with Twins' accuracy dropping from 80.57% to 62.40%.

Accelerated Alternating Minimization for X-ray Tomographic Reconstruction

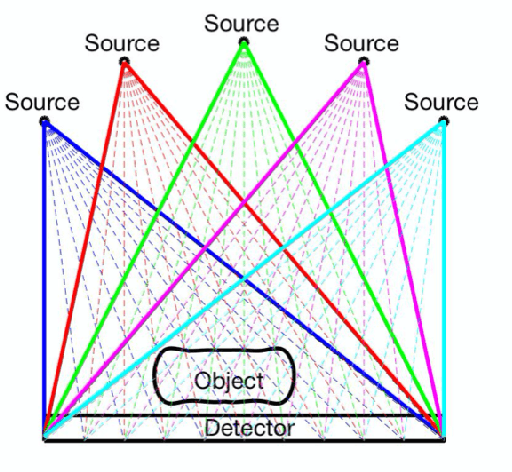
While Computerized Tomography (CT) images can help detect disease such as Covid-19, regular CT machines are large and expensive. Cheaper and more portable machines suffer from errors in geometry acquisition that downgrades CT image quality. The errors in geometry can be represented with parameters in the mathematical model for image reconstruction. To obtain a good image, we formulate a nonlinear least squares problem that simultaneously reconstructs the image and corrects for errors in the geometry parameters. We develop an accelerated alternating minimization scheme to reconstruct the image and geometry parameters.