Scaling-up Diverse Orthogonal Convolutional Networks with a Paraunitary Framework
Paper and Code
Jun 16, 2021
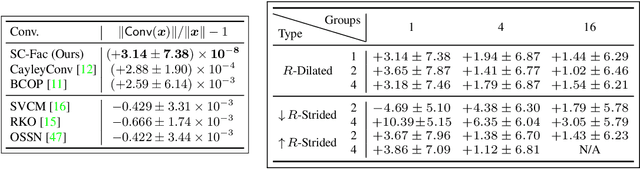
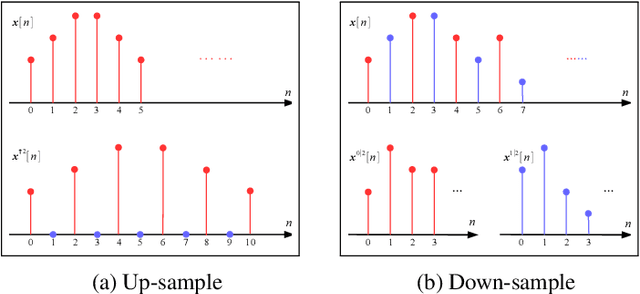
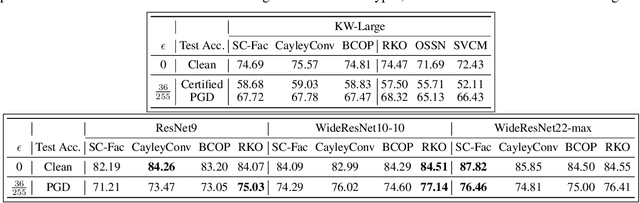
Enforcing orthogonality in neural networks is an antidote for gradient vanishing/exploding problems, sensitivity by adversarial perturbation, and bounding generalization errors. However, many previous approaches are heuristic, and the orthogonality of convolutional layers is not systematically studied: some of these designs are not exactly orthogonal, while others only consider standard convolutional layers and propose specific classes of their realizations. To address this problem, we propose a theoretical framework for orthogonal convolutional layers, which establishes the equivalence between various orthogonal convolutional layers in the spatial domain and the paraunitary systems in the spectral domain. Since there exists a complete spectral factorization of paraunitary systems, any orthogonal convolution layer can be parameterized as convolutions of spatial filters. Our framework endows high expressive power to various convolutional layers while maintaining their exact orthogonality. Furthermore, our layers are memory and computationally efficient for deep networks compared to previous designs. Our versatile framework, for the first time, enables the study of architecture designs for deep orthogonal networks, such as choices of skip connection, initialization, stride, and dilation. Consequently, we scale up orthogonal networks to deep architectures, including ResNet, WideResNet, and ShuffleNet, substantially increasing the performance over the traditional shallow orthogonal networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge