How Neural Networks Extrapolate: From Feedforward to Graph Neural Networks

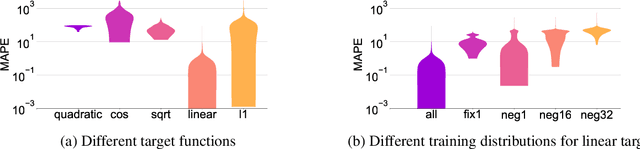
We study how neural networks trained by gradient descent extrapolate, i.e., what they learn outside the support of the training distribution. Previous works report mixed empirical results when extrapolating with neural networks: while multilayer perceptrons (MLPs) do not extrapolate well in certain simple tasks, Graph Neural Network (GNN), a structured network with MLP modules, has shown some success in more complex tasks. Working towards a theoretical explanation, we identify conditions under which MLPs and GNNs extrapolate well. First, we quantify the observation that ReLU MLPs quickly converge to linear functions along any direction from the origin, which implies that ReLU MLPs do not extrapolate most non-linear functions. But, they can provably learn a linear target function when the training distribution is sufficiently "diverse". Second, in connection to analyzing successes and limitations of GNNs, these results suggest a hypothesis for which we provide theoretical and empirical evidence: the success of GNNs in extrapolating algorithmic tasks to new data (e.g., larger graphs or edge weights) relies on encoding task-specific non-linearities in the architecture or features.