Imane Hafnaoui
Subspace Determination through Local Intrinsic Dimensional Decomposition: Theory and Experimentation
Jul 15, 2019
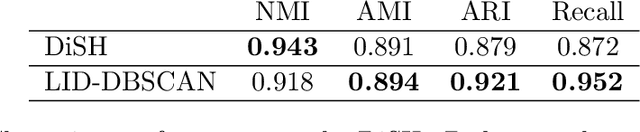

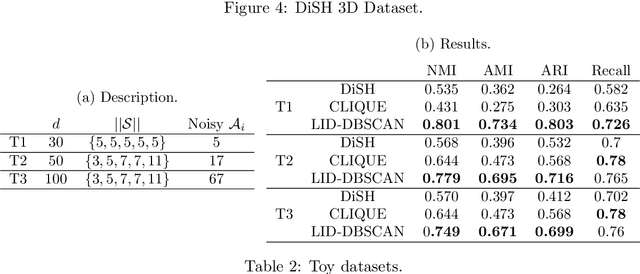
Abstract:Axis-aligned subspace clustering generally entails searching through enormous numbers of subspaces (feature combinations) and evaluation of cluster quality within each subspace. In this paper, we tackle the problem of identifying subsets of features with the most significant contribution to the formation of the local neighborhood surrounding a given data point. For each point, the recently-proposed Local Intrinsic Dimension (LID) model is used in identifying the axis directions along which features have the greatest local discriminability, or equivalently, the fewest number of components of LID that capture the local complexity of the data. In this paper, we develop an estimator of LID along axis projections, and provide preliminary evidence that this LID decomposition can indicate axis-aligned data subspaces that support the formation of clusters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge