Measuring and Controlling Divisiveness in Rank Aggregation

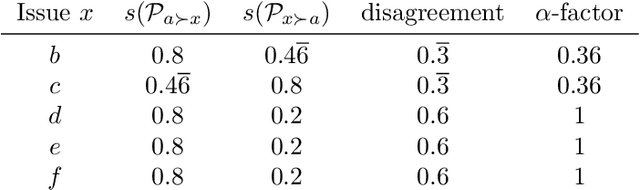
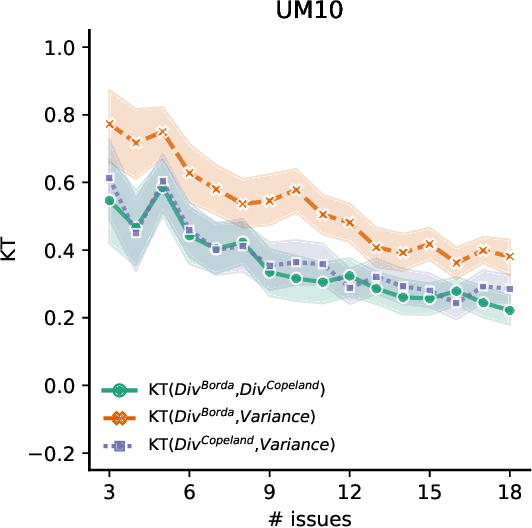
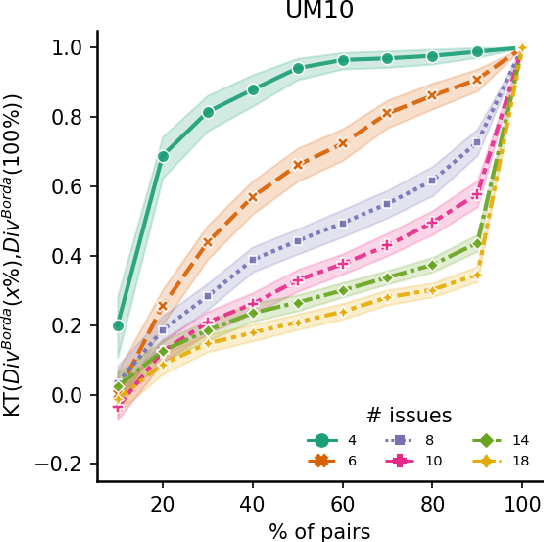
In rank aggregation, members of a population rank issues to decide which are collectively preferred. We focus instead on identifying divisive issues that express disagreements among the preferences of individuals. We analyse the properties of our divisiveness measures and their relation to existing notions of polarisation. We also study their robustness under incomplete preferences and algorithms for control and manipulation of divisiveness. Our results advance our understanding of how to quantify disagreements in collective decision-making.

Measuring a Priori Voting Power -- Taking Delegations Seriously

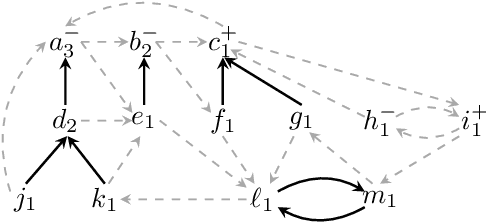
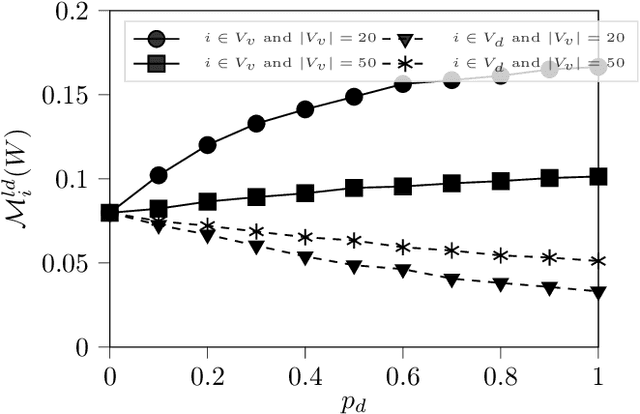
In this paper, we introduce new power indices to measure the criticality of voters involved in different elections where delegations play a key role, namely, two variants of the proxy voting setting and a liquid democracy setting. First, we argue that our power indices are natural extensions of the Penrose-Banzhaf index in classic simple voting games, illustrating their intuitions. We show that recursive formulas can compute these indices for weighted voting games in pseudo-polynomial time. Last, we highlight theoretical properties and provide numerical results to illustrate how introducing delegation options modifies the voting power of voters.

Collective discrete optimisation as judgment aggregation

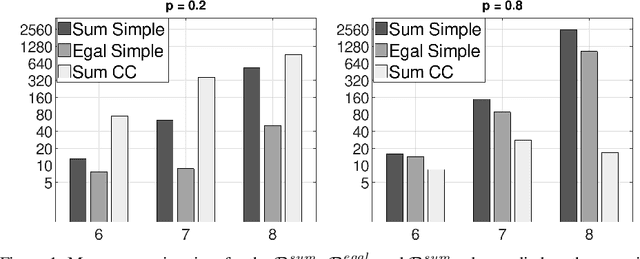
Many important collective decision-making problems can be seen as multi-agent versions of discrete optimisation problems. Participatory budgeting, for instance, is the collective version of the knapsack problem; other examples include collective scheduling, and collective spanning trees. Rather than developing a specific model, as well as specific algorithmic techniques, for each of these problems, we propose to represent and solve them in the unifying framework of judgment aggregation with weighted issues. We provide a modular definition of collective discrete optimisation (CDO) rules based on coupling a set scoring function with an operator, and we show how they generalise several existing procedures developed for specific CDO problems. We also give an implementation based on integer linear programming (ILP) and test it on the problem of collective spanning trees.

Unravelling multi-agent ranked delegations

We introduce a voting model with multi-agent ranked delegations. This model generalises liquid democracy in two aspects: first, an agent's delegation can use the votes of multiple other agents to determine their own -- for instance, an agent's vote may correspond to the majority outcome of the votes of a trusted group of agents; second, agents can submit a ranking over multiple delegations, so that a backup delegation can be used when their preferred delegations are involved in cycles. The main focus of this paper is the study of unravelling procedures that transform the delegation ballots received from the agents into a profile of direct votes, from which a winning alternative can then be determined by using a standard voting rule. We propose and study six such unravelling procedures, two based on optimisation and four using a greedy approach. We study both algorithmic and axiomatic properties, as well as related computational complexity problems of our unravelling procedures for different restrictions on the types of ballots that the agents can submit.