Collective discrete optimisation as judgment aggregation

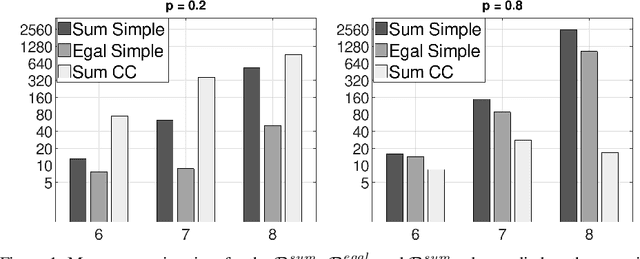
Many important collective decision-making problems can be seen as multi-agent versions of discrete optimisation problems. Participatory budgeting, for instance, is the collective version of the knapsack problem; other examples include collective scheduling, and collective spanning trees. Rather than developing a specific model, as well as specific algorithmic techniques, for each of these problems, we propose to represent and solve them in the unifying framework of judgment aggregation with weighted issues. We provide a modular definition of collective discrete optimisation (CDO) rules based on coupling a set scoring function with an operator, and we show how they generalise several existing procedures developed for specific CDO problems. We also give an implementation based on integer linear programming (ILP) and test it on the problem of collective spanning trees.

Unravelling multi-agent ranked delegations

We introduce a voting model with multi-agent ranked delegations. This model generalises liquid democracy in two aspects: first, an agent's delegation can use the votes of multiple other agents to determine their own -- for instance, an agent's vote may correspond to the majority outcome of the votes of a trusted group of agents; second, agents can submit a ranking over multiple delegations, so that a backup delegation can be used when their preferred delegations are involved in cycles. The main focus of this paper is the study of unravelling procedures that transform the delegation ballots received from the agents into a profile of direct votes, from which a winning alternative can then be determined by using a standard voting rule. We propose and study six such unravelling procedures, two based on optimisation and four using a greedy approach. We study both algorithmic and axiomatic properties, as well as related computational complexity problems of our unravelling procedures for different restrictions on the types of ballots that the agents can submit.

Relaxing Exclusive Control in Boolean Games

In the typical framework for boolean games (BG) each player can change the truth value of some propositional atoms, while attempting to make her goal true. In standard BG goals are propositional formulas, whereas in iterated BG goals are formulas of Linear Temporal Logic. Both notions of BG are characterised by the fact that agents have exclusive control over their set of atoms, meaning that no two agents can control the same atom. In the present contribution we drop the exclusivity assumption and explore structures where an atom can be controlled by multiple agents. We introduce Concurrent Game Structures with Shared Propositional Control (CGS-SPC) and show that they ac- count for several classes of repeated games, including iterated boolean games, influence games, and aggregation games. Our main result shows that, as far as verification is concerned, CGS-SPC can be reduced to concurrent game structures with exclusive control. This result provides a polynomial reduction for the model checking problem of specifications in Alternating-time Temporal Logic on CGS-SPC.