Discounting in Strategy Logic

Discounting is an important dimension in multi-agent systems as long as we want to reason about strategies and time. It is a key aspect in economics as it captures the intuition that the far-away future is not as important as the near future. Traditional verification techniques allow to check whether there is a winning strategy for a group of agents but they do not take into account the fact that satisfying a goal sooner is different from satisfying it after a long wait. In this paper, we augment Strategy Logic with future discounting over a set of discounted functions D, denoted SLdisc[D]. We consider "until" operators with discounting functions: the satisfaction value of a specification in SLdisc[D] is a value in [0, 1], where the longer it takes to fulfill requirements, the smaller the satisfaction value is. We motivate our approach with classical examples from Game Theory and study the complexity of model-checking SLdisc[D]-formulas.

Reasoning about Human-Friendly Strategies in Repeated Keyword Auctions

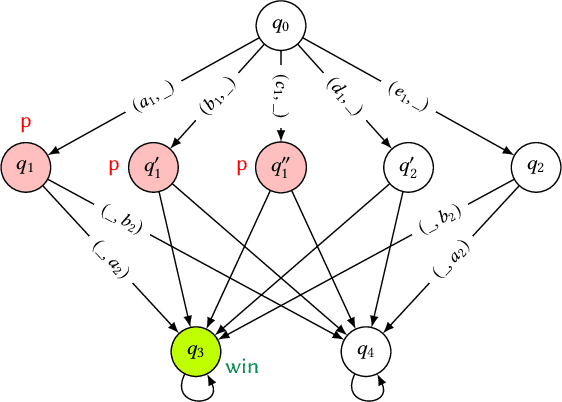
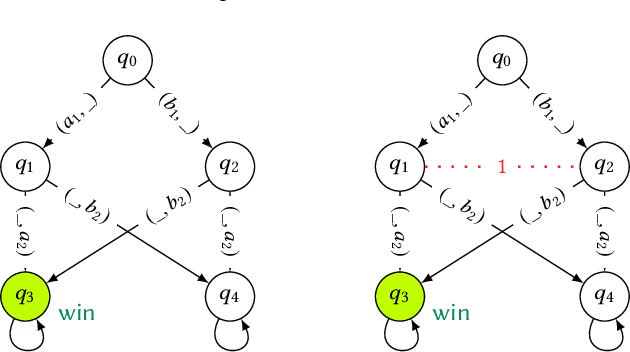
In online advertising, search engines sell ad placements for keywords continuously through auctions. This problem can be seen as an infinitely repeated game since the auction is executed whenever a user performs a query with the keyword. As advertisers may frequently change their bids, the game will have a large set of equilibria with potentially complex strategies. In this paper, we propose the use of natural strategies for reasoning in such setting as they are processable by artificial agents with limited memory and/or computational power as well as understandable by human users. To reach this goal, we introduce a quantitative version of Strategy Logic with natural strategies in the setting of imperfect information. In a first step, we show how to model strategies for repeated keyword auctions and take advantage of the model for proving properties evaluating this game. In a second step, we study the logic in relation to the distinguishing power, expressivity, and model-checking complexity for strategies with and without recall.

A General Framework for the Logical Representation of Combinatorial Exchange Protocols

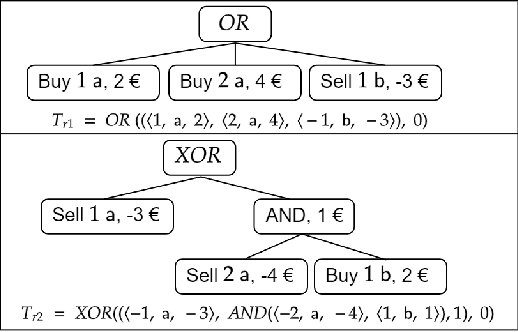
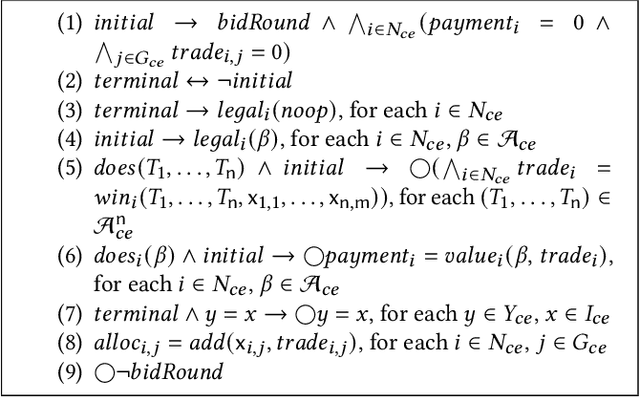
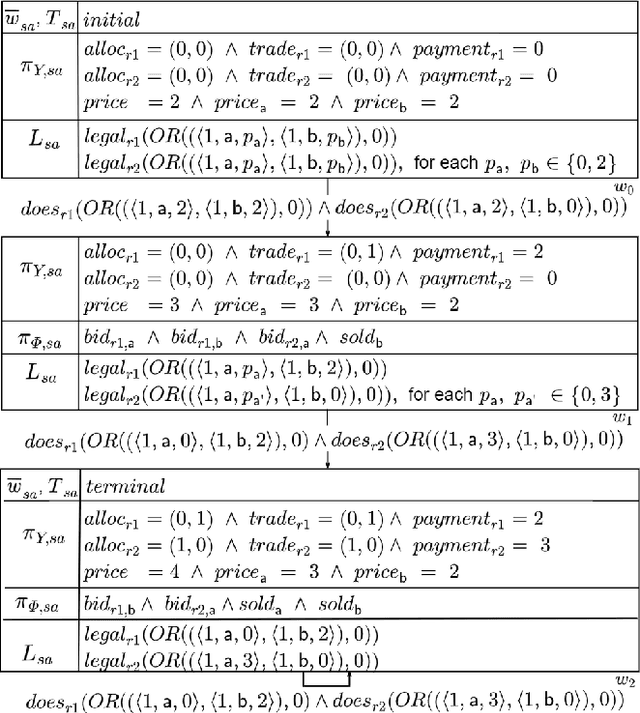
The goal of this paper is to propose a framework for representing and reasoning about the rules governing a combinatorial exchange. Such a framework is at first interest as long as we want to build up digital marketplaces based on auction, a widely used mechanism for automated transactions. Combinatorial exchange is the most general case of auctions, mixing the double and combinatorial variants: agents bid to trade bundles of goods. Hence the framework should fulfill two requirements: (i) it should enable bidders to express their bids on combinations of goods and (ii) it should allow describing the rules governing some market, namely the legal bids, the allocation and payment rules. To do so, we define a logical language in the spirit of the Game Description Language: the Combinatorial Exchange Description Language is the first language for describing combinatorial exchange in a logical framework. The contribution is two-fold: first, we illustrate the general dimension by representing different kinds of protocols, and second, we show how to reason about auction properties in this machine-processable language.

Game Description Logic with Integers: A GDL Numerical Extension

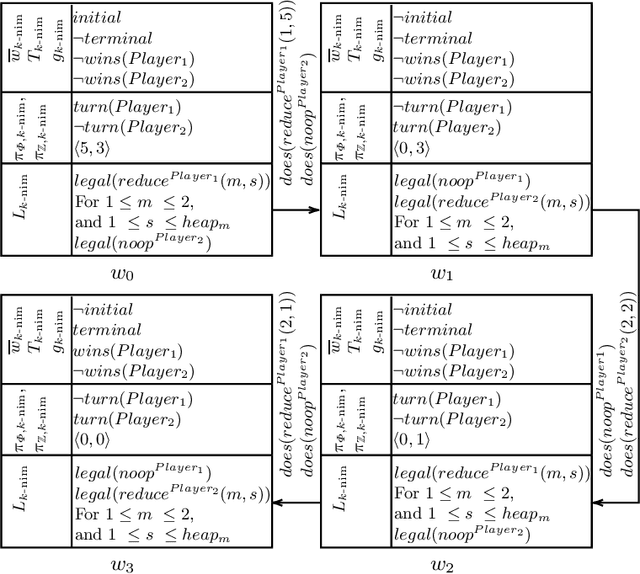
Many problems can be viewed as games, where one or more agents try to ensure that certain objectives hold no matter the behavior from the environment and other agents. In recent years, a number of logical formalisms have been proposed for specifying games among which the Game Description Language (GDL) was established as the official language for General Game Playing. Although numbers are recurring in games, the description of games with numerical features in GDL requires the enumeration from all possible numeric values and the relation among them. Thereby, in this paper, we introduce the Game Description Logic with Integers (GDLZ) to describe games with numerical variables, numerical parameters, as well as to perform numerical comparisons. We compare our approach with GDL and show that when describing the same game, GDLZ is more compact.

Refining HTN Methods via Task Insertion with Preferences

Hierarchical Task Network (HTN) planning is showing its power in real-world planning. Although domain experts have partial hierarchical domain knowledge, it is time-consuming to specify all HTN methods, leaving them incomplete. On the other hand, traditional HTN learning approaches focus only on declarative goals, omitting the hierarchical domain knowledge. In this paper, we propose a novel learning framework to refine HTN methods via task insertion with completely preserving the original methods. As it is difficult to identify incomplete methods without designating declarative goals for compound tasks, we introduce the notion of prioritized preference to capture the incompleteness possibility of methods. Specifically, the framework first computes the preferred completion profile w.r.t. the prioritized preference to refine the incomplete methods. Then it finds the minimal set of refined methods via a method substitution operation. Experimental analysis demonstrates that our approach is effective, especially in solving new HTN planning instances.

Relaxing Exclusive Control in Boolean Games

In the typical framework for boolean games (BG) each player can change the truth value of some propositional atoms, while attempting to make her goal true. In standard BG goals are propositional formulas, whereas in iterated BG goals are formulas of Linear Temporal Logic. Both notions of BG are characterised by the fact that agents have exclusive control over their set of atoms, meaning that no two agents can control the same atom. In the present contribution we drop the exclusivity assumption and explore structures where an atom can be controlled by multiple agents. We introduce Concurrent Game Structures with Shared Propositional Control (CGS-SPC) and show that they ac- count for several classes of repeated games, including iterated boolean games, influence games, and aggregation games. Our main result shows that, as far as verification is concerned, CGS-SPC can be reduced to concurrent game structures with exclusive control. This result provides a polynomial reduction for the model checking problem of specifications in Alternating-time Temporal Logic on CGS-SPC.

Knowledge Sharing in Coalitions

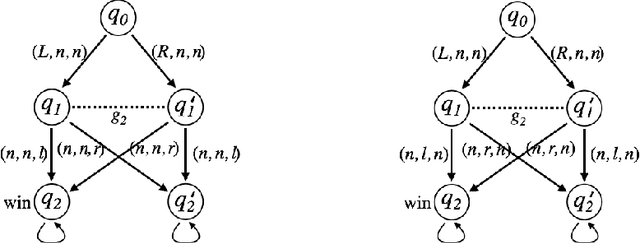
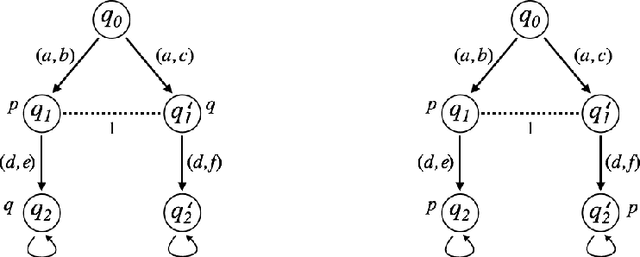
The aim of this paper is to investigate the interplay between knowledge shared by a group of agents and its coalition ability. We investigate this relation in the standard context of imperfect information concurrent game. We assume that whenever a set of agents form a coalition to achieve a goal, they share their knowledge before acting. Based on this assumption, we propose a new semantics for alternating-time temporal logic with imperfect information and perfect recall. It turns out that this semantics is sufficient to preserve all the desirable properties of coalition ability in traditional coalitional logics. Meanwhile, we investigate how knowledge sharing within a group of agents contributes to its coalitional ability through the interplay of epistemic and coalition modalities. This work provides a partial answer to the question: which kind of group knowledge is required for a group to achieve their goals in the context of imperfect information.

Strategic disclosure of opinions on a social network

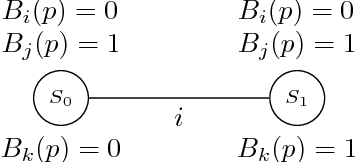
We study the strategic aspects of social influence in a society of agents linked by a trust network, introducing a new class of games called games of influence. A game of influence is an infinite repeated game with incomplete information in which, at each stage of interaction, an agent can make her opinions visible (public) or invisible (private) in order to influence other agents' opinions. The influence process is mediated by a trust network, as we assume that the opinion of a given agent is only affected by the opinions of those agents that she considers trustworthy (i.e., the agents in the trust network that are directly linked to her). Each agent is endowed with a goal, expressed in a suitable temporal language inspired from linear temporal logic (LTL). We show that games of influence provide a simple abstraction to explore the effects of the trust network structure on the agents' behaviour, by considering solution concepts from game-theory such as Nash equilibrium, weak dominance and winning strategies.