Thou Shalt not Pick all Items if Thou are First: of Strategyproof and Fair Picking Sequences

When allocating indivisible items to agents, it is known that the only strategyproof mechanisms that satisfy a set of rather mild conditions are constrained serial dictatorships: given a fixed order over agents, at each step the designated agent chooses a given number of items (depending on her position in the sequence). With these rules, also known as non-interleaving picking sequences, agents who come earlier in the sequence have a larger choice of items. However, this advantage can be compensated by a higher number of items received by those who come later. How to balance priority in the sequence and number of items received is a nontrivial question. We use a previous model, parameterized by a mapping from ranks to scores, a social welfare functional, and a distribution over preference profiles. For several meaningful choices of parameters, we show that the optimal sequence can be computed in polynomial time. Last, we give a simple procedure for eliciting scoring vectors and we study the impact of the assignment from agents to positions on the ex-post social welfare.

A General Framework for the Logical Representation of Combinatorial Exchange Protocols

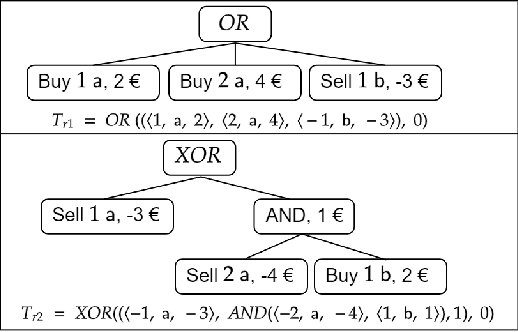
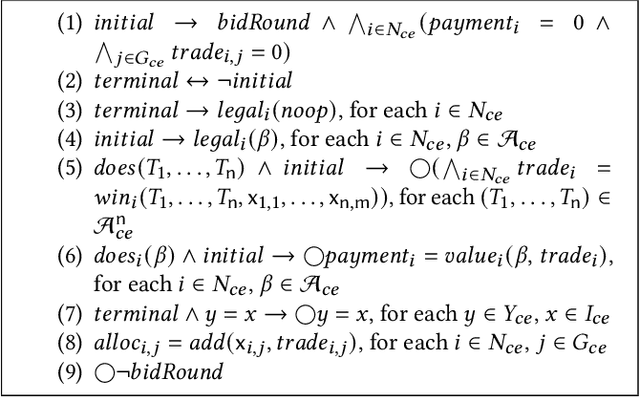
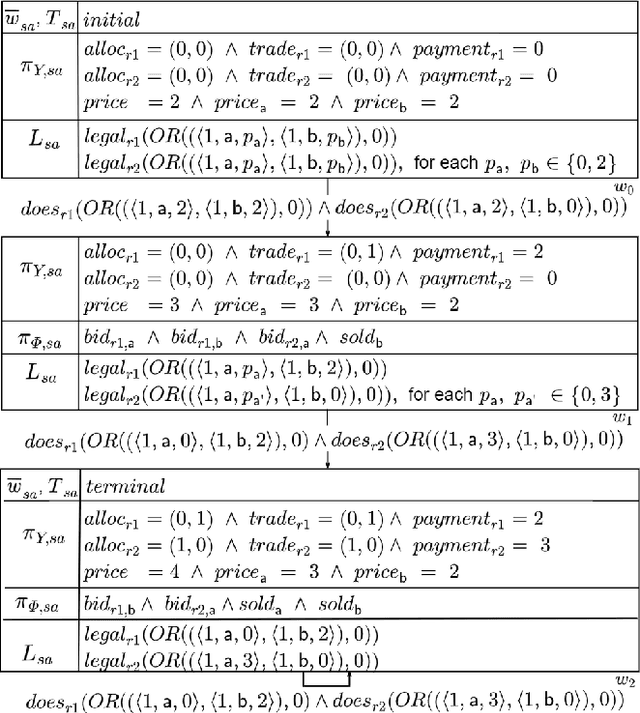
The goal of this paper is to propose a framework for representing and reasoning about the rules governing a combinatorial exchange. Such a framework is at first interest as long as we want to build up digital marketplaces based on auction, a widely used mechanism for automated transactions. Combinatorial exchange is the most general case of auctions, mixing the double and combinatorial variants: agents bid to trade bundles of goods. Hence the framework should fulfill two requirements: (i) it should enable bidders to express their bids on combinations of goods and (ii) it should allow describing the rules governing some market, namely the legal bids, the allocation and payment rules. To do so, we define a logical language in the spirit of the Game Description Language: the Combinatorial Exchange Description Language is the first language for describing combinatorial exchange in a logical framework. The contribution is two-fold: first, we illustrate the general dimension by representing different kinds of protocols, and second, we show how to reason about auction properties in this machine-processable language.

Multi-agent simulation of voter's behaviour

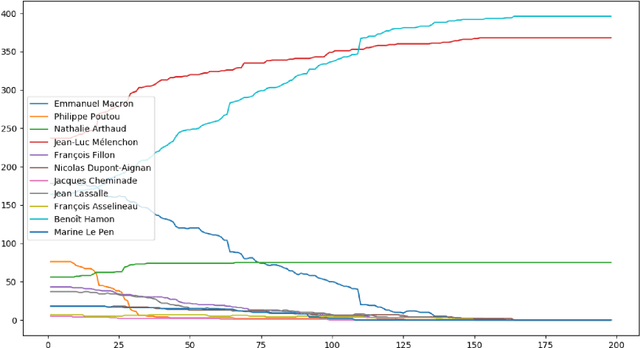
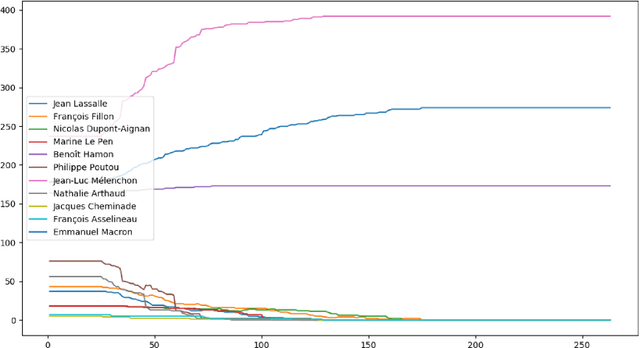
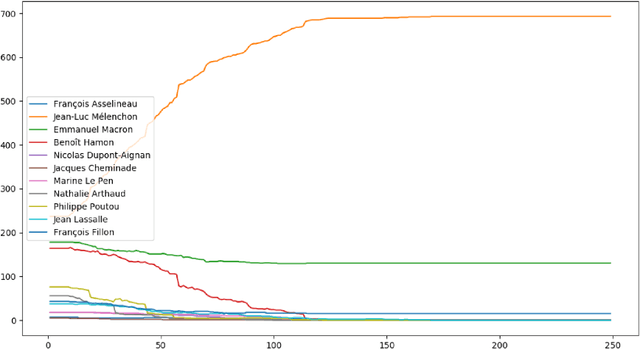
The goal of this paper is to simulate the voters behaviour given a voting method. Our approach uses a multi-agent simulation in order to model a voting process through many iterations, so that the voters can vote by taking into account the results of polls. Here we only tried basic rules and a single voting method, but further attempts could explore new features.

Fair in the Eyes of Others

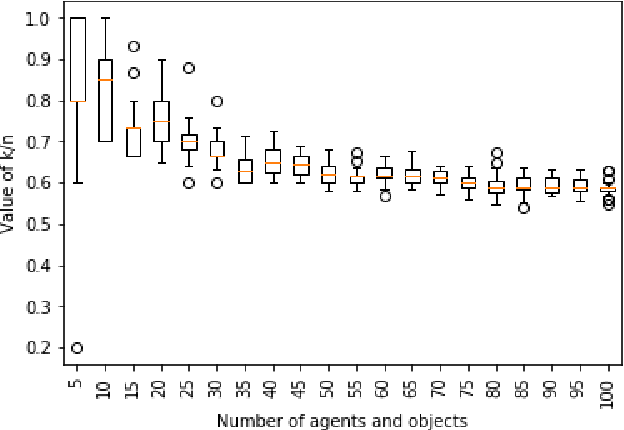
Envy-freeness is a widely studied notion in resource allocation, capturing some aspects of fairness. The notion of envy being inherently subjective though, it might be the case that an agent envies another agent, but that she objectively has no reason to do so. The difficulty here is to define the notion of objectivity, since no ground-truth can properly serve as a basis of this definition. A natural approach is to consider the judgement of the other agents as a proxy for objectivity. Building on previous work by Parijs (who introduced "unanimous envy") we propose the notion of approval envy: an agent $a_i$ experiences approval envy towards $a_j$ if she is envious of $a_j$, and sufficiently many agents agree that this should be the case, from their own perspectives. Some interesting properties of this notion are put forward. Computing the minimal threshold guaranteeing approval envy clearly inherits well-known intractable results from envy-freeness, but (i) we identify some tractable cases such as house allocation; and (ii) we provide a general method based on a mixed integer programming encoding of the problem, which proves to be efficient in practice. This allows us in particular to show experimentally that existence of such allocations, with a rather small threshold, is very often observed.

Chore division on a graph

The paper considers fair allocation of indivisible nondisposable items that generate disutility (chores). We assume that these items are placed in the vertices of a graph and each agent's share has to form a connected subgraph of this graph. Although a similar model has been investigated before for goods, we show that the goods and chores settings are inherently different. In particular, it is impossible to derive the solution of the chores instance from the solution of its naturally associated fair division instance. We consider three common fair division solution concepts, namely proportionality, envy-freeness and equitability, and two individual disutility aggregation functions: additive and maximum based. We show that deciding the existence of a fair allocation is hard even if the underlying graph is a path or a star. We also present some efficiently solvable special cases for these graph topologies.

Efficiency, Sequenceability and Deal-Optimality in Fair Division of Indivisible Goods

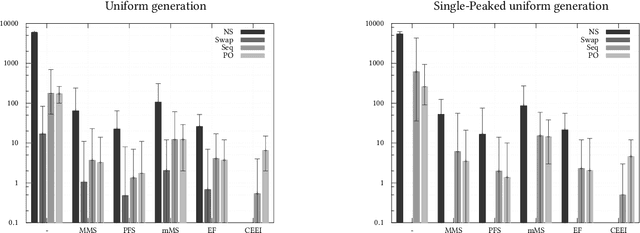
In fair division of indivisible goods, using sequences of sincere choices (or picking sequences) is a natural way to allocate the objects. The idea is as follows: at each stage, a designated agent picks one object among those that remain. Another intuitive way to obtain an allocation is to give objects to agents in the first place, and to let agents exchange them as long as such "deals" are beneficial. This paper investigates these notions, when agents have additive preferences over objects, and unveils surprising connections between them, and with other efficiency and fairness notions. In particular, we show that an allocation is sequenceable iff it is optimal for a certain type of deals, namely cycle deals involving a single object. Furthermore, any Pareto-optimal allocation is sequenceable, but not the converse. Regarding fairness, we show that an allocation can be envy-free and non-sequenceable, but that every competitive equilibrium with equal incomes is sequenceable. To complete the picture, we show how some domain restrictions may affect the relations between these notions. Finally, we experimentally explore the links between the scales of efficiency and fairness.

Efficiency and Sequenceability in Fair Division of Indivisible Goods with Additive Preferences

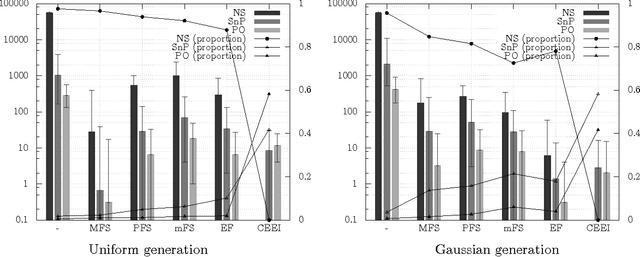
In fair division of indivisible goods, using sequences of sincere choices (or picking sequences) is a natural way to allocate the objects. The idea is the following: at each stage, a designated agent picks one object among those that remain. This paper, restricted to the case where the agents have numerical additive preferences over objects, revisits to some extent the seminal paper by Brams and King [9] which was specific to ordinal and linear order preferences over items. We point out similarities and differences with this latter context. In particular, we show that any Pareto-optimal allocation (under additive preferences) is sequenceable, but that the converse is not true anymore. This asymmetry leads naturally to the definition of a "scale of efficiency" having three steps: Pareto-optimality, sequenceability without Pareto-optimality, and non-sequenceability. Finally, we investigate the links between these efficiency properties and the "scale of fairness" we have described in an earlier work [7]: we first show that an allocation can be envy-free and non-sequenceable, but that every competitive equilibrium with equal incomes is sequenceable. Then we experimentally explore the links between the scales of efficiency and fairness.