Natural Strategic Ability in Stochastic Multi-Agent Systems

Strategies synthesized using formal methods can be complex and often require infinite memory, which does not correspond to the expected behavior when trying to model Multi-Agent Systems (MAS). To capture such behaviors, natural strategies are a recently proposed framework striking a balance between the ability of agents to strategize with memory and the model-checking complexity, but until now has been restricted to fully deterministic settings. For the first time, we consider the probabilistic temporal logics PATL and PATL* under natural strategies (NatPATL and NatPATL*, resp.). As main result we show that, in stochastic MAS, NatPATL model-checking is NP-complete when the active coalition is restricted to deterministic strategies. We also give a 2NEXPTIME complexity result for NatPATL* with the same restriction. In the unrestricted case, we give an EXPSPACE complexity for NatPATL and 3EXPSPACE complexity for NatPATL*.

Discounting in Strategy Logic

Discounting is an important dimension in multi-agent systems as long as we want to reason about strategies and time. It is a key aspect in economics as it captures the intuition that the far-away future is not as important as the near future. Traditional verification techniques allow to check whether there is a winning strategy for a group of agents but they do not take into account the fact that satisfying a goal sooner is different from satisfying it after a long wait. In this paper, we augment Strategy Logic with future discounting over a set of discounted functions D, denoted SLdisc[D]. We consider "until" operators with discounting functions: the satisfaction value of a specification in SLdisc[D] is a value in [0, 1], where the longer it takes to fulfill requirements, the smaller the satisfaction value is. We motivate our approach with classical examples from Game Theory and study the complexity of model-checking SLdisc[D]-formulas.

Reasoning about Human-Friendly Strategies in Repeated Keyword Auctions

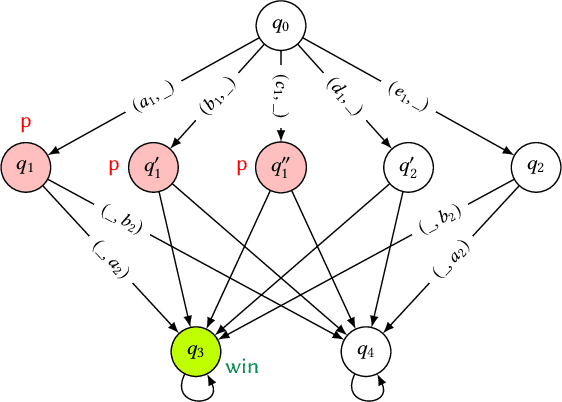
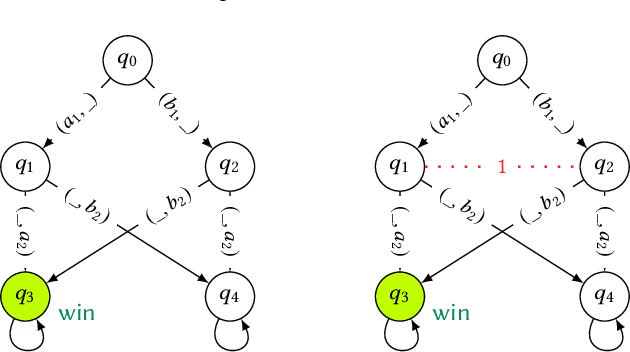
In online advertising, search engines sell ad placements for keywords continuously through auctions. This problem can be seen as an infinitely repeated game since the auction is executed whenever a user performs a query with the keyword. As advertisers may frequently change their bids, the game will have a large set of equilibria with potentially complex strategies. In this paper, we propose the use of natural strategies for reasoning in such setting as they are processable by artificial agents with limited memory and/or computational power as well as understandable by human users. To reach this goal, we introduce a quantitative version of Strategy Logic with natural strategies in the setting of imperfect information. In a first step, we show how to model strategies for repeated keyword auctions and take advantage of the model for proving properties evaluating this game. In a second step, we study the logic in relation to the distinguishing power, expressivity, and model-checking complexity for strategies with and without recall.

A General Framework for the Logical Representation of Combinatorial Exchange Protocols

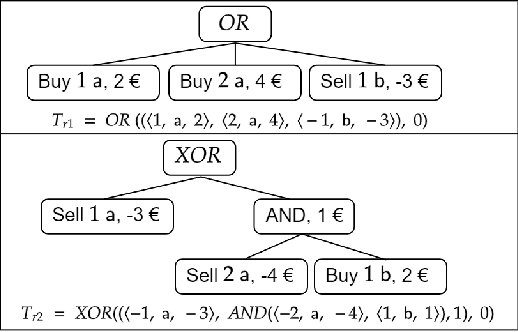
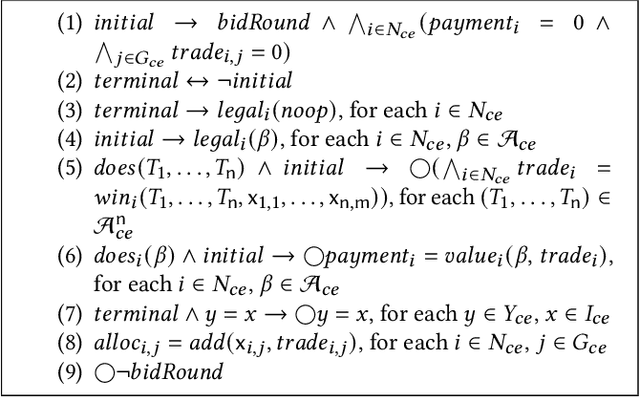
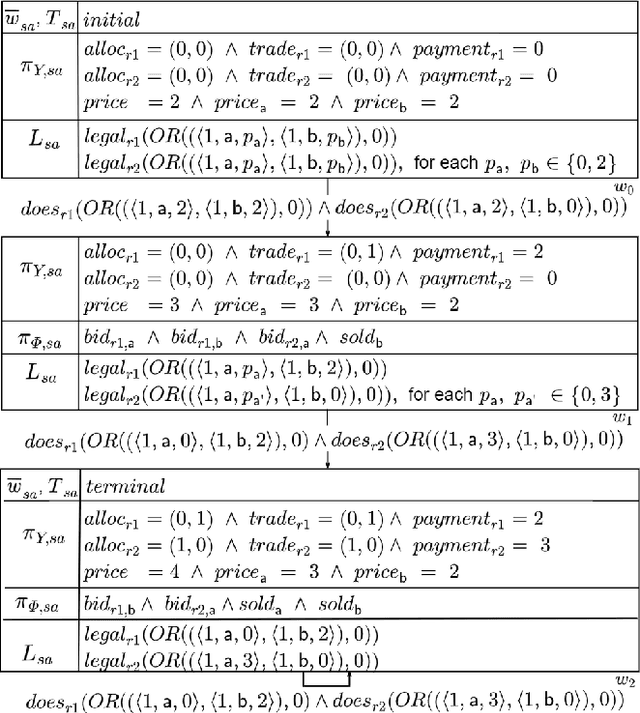
The goal of this paper is to propose a framework for representing and reasoning about the rules governing a combinatorial exchange. Such a framework is at first interest as long as we want to build up digital marketplaces based on auction, a widely used mechanism for automated transactions. Combinatorial exchange is the most general case of auctions, mixing the double and combinatorial variants: agents bid to trade bundles of goods. Hence the framework should fulfill two requirements: (i) it should enable bidders to express their bids on combinations of goods and (ii) it should allow describing the rules governing some market, namely the legal bids, the allocation and payment rules. To do so, we define a logical language in the spirit of the Game Description Language: the Combinatorial Exchange Description Language is the first language for describing combinatorial exchange in a logical framework. The contribution is two-fold: first, we illustrate the general dimension by representing different kinds of protocols, and second, we show how to reason about auction properties in this machine-processable language.

Game Description Logic with Integers: A GDL Numerical Extension

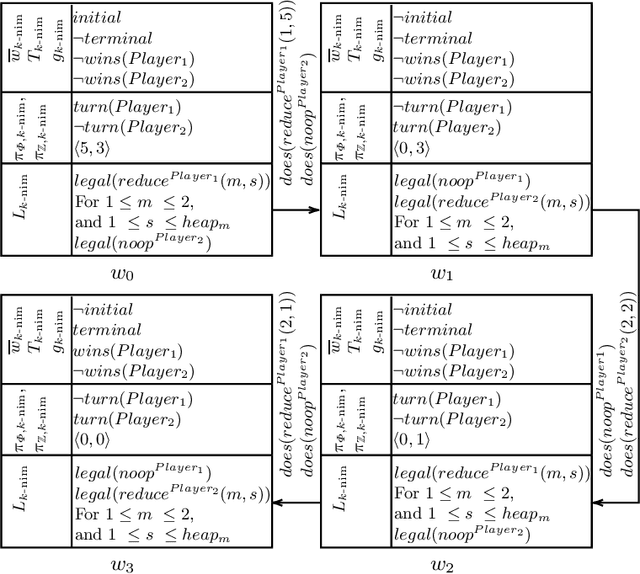
Many problems can be viewed as games, where one or more agents try to ensure that certain objectives hold no matter the behavior from the environment and other agents. In recent years, a number of logical formalisms have been proposed for specifying games among which the Game Description Language (GDL) was established as the official language for General Game Playing. Although numbers are recurring in games, the description of games with numerical features in GDL requires the enumeration from all possible numeric values and the relation among them. Thereby, in this paper, we introduce the Game Description Logic with Integers (GDLZ) to describe games with numerical variables, numerical parameters, as well as to perform numerical comparisons. We compare our approach with GDL and show that when describing the same game, GDLZ is more compact.