Translating Natural Language to Strategic Temporal Specifications via LLMs

A rigorous formalization of system requirements is a fundamental prerequisite for the verification of Multi-Agent Systems (MAS). However, writing correct formal specifications is well known as an error-prone, time-consuming, and expertise-intensive task. This difficulty is further accentuated in MAS, where requirements must capture strategic abilities and temporal objectives. At present, there is no established methodology for deriving MAS specifications from natural language. We present a framework for translating Natural Language descriptions of strategic requirements into well-formed ATL/ATL* formulas using Large Language Models (LLMs). Since no available dataset supports supervised learning for the NL-to-ATL/ATL* translation task, we create and curate a novel expert-validated dataset, employed for training and evaluating fine-tuned models. On a held-out test set, evaluated under the LLM judge that best agrees with expert annotations, in-domain fine-tuning of small open-weight models (3 - 7B parameters) matches strong few-shot proprietary API baselines. Our best fine-tuned system reaches 0.84 semantic accuracy, statistically on par with 0.86 for the strongest few-shot proprietary baseline, while keeping requirements on-premises. We further find that judge reliability is inverse to generator strength. The open-weight Llama-3.3-70B tracks human verdicts most closely, whereas the strongest proprietary models are the least reliable judges, over-rejecting faithful paraphrases of the reference. To assess the practical applicability of the generated specifications, we embed our tool to an existing strategic logics model checker, enabling non-expert users to specify strategic properties in natural language.

A Neuro-Symbolic Approach to Strategy Synthesis for Strategic Logics

Reasoning about what agents can achieve through strategic interaction is a core challenge in Multi-Agent Systems (MAS). Logics for strategic ability, such as ATL, provide rigorous methods, but their adoption is often hindered by the computational cost of strategy synthesis. We introduce a neuro-symbolic framework that integrates large language models (LLMs) into the model-checking pipeline for MAS. The LLM acts as a strategy-generation oracle, proposing candidate strategies that are then formally validated by a standard MAS model checker. This generate-and-certify architecture uses LLM guidance to navigate large combinatorial strategy spaces while preserving formal soundness: generated strategies are accepted only when certified by the verifier. We instantiate the framework for bounded strategic reasoning in NatATL and introduce the first NatATL strategy-synthesis dataset, consisting of 4211 instances. Experiments with an open-weight Qwen3-32B model show that our certified pipeline achieves 92\% accuracy on strategy-synthesis outcomes.

3vLTL: A Tool to Generate Automata for Three-valued LTL

Multi-valued logics have a long tradition in the literature on system verification, including run-time verification. However, comparatively fewer model-checking tools have been developed for multi-valued specification languages. We present 3vLTL, a tool to generate Buchi automata from formulas in Linear-time Temporal Logic (LTL) interpreted on a three-valued semantics. Given an LTL formula, a set of atomic propositions as the alphabet for the automaton, and a truth value, our procedure generates a Buchi automaton that accepts all the words that assign the chosen truth value to the LTL formula. Given the particular type of the output of the tool, it can also be seamlessly processed by third-party libraries in a natural way. That is, the Buchi automaton can then be used in the context of formal verification to check whether an LTL formula is true, false, or undefined on a given model.

Reasoning about Intuitionistic Computation Tree Logic

In this paper, we define an intuitionistic version of Computation Tree Logic. After explaining the semantic features of intuitionistic logic, we examine how these characteristics can be interesting for formal verification purposes. Subsequently, we define the syntax and semantics of our intuitionistic version of CTL and study some simple properties of the so obtained logic. We conclude by demonstrating that some fixed-point axioms of CTL are not valid in the intuitionistic version of CTL we have defined.

Model Checking Strategic Abilities in Information-sharing Systems

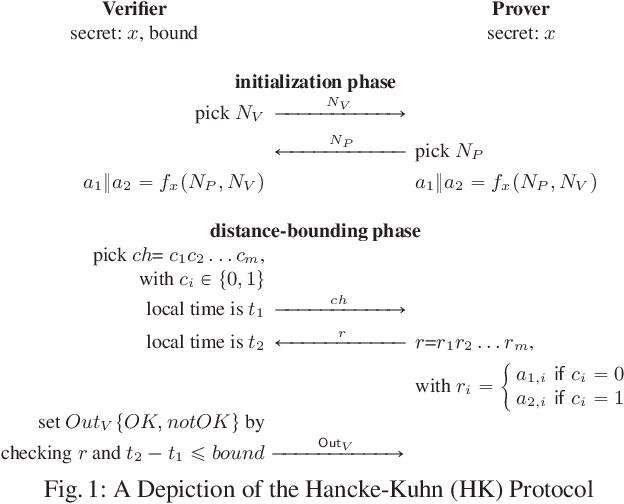
We introduce a subclass of concurrent game structures (CGS) with imperfect information in which agents are endowed with private data-sharing capabilities. Importantly, our CGSs are such that it is still decidable to model-check these CGSs against a relevant fragment of ATL. These systems can be thought as a generalisation of architectures allowing information forks, in the sense that, in the initial states of the system, we allow information forks from agents outside a given set A to agents inside this A. For this reason, together with the fact that the communication in our models underpins a specialised form of broadcast, we call our formalism A-cast systems. To underline, the fragment of ATL for which we show the model-checking problem to be decidable over A-cast is a large and significant one; it expresses coalitions over agents in any subset of the set A. Indeed, as we show, our systems and this ATL fragments can encode security problems that are notoriously hard to express faithfully: terrorist-fraud attacks in identity schemes.

Reasoning about Human-Friendly Strategies in Repeated Keyword Auctions

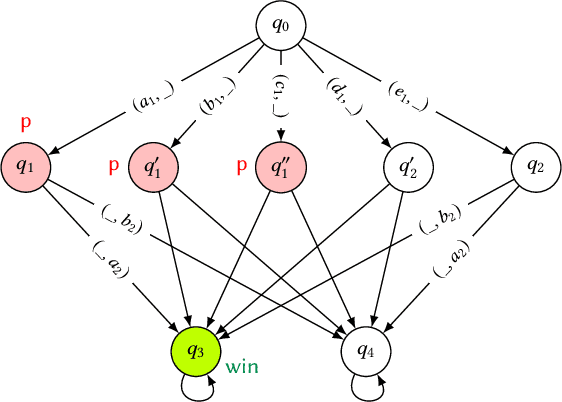
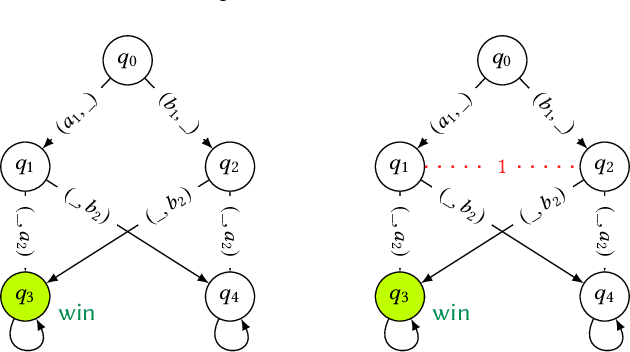
In online advertising, search engines sell ad placements for keywords continuously through auctions. This problem can be seen as an infinitely repeated game since the auction is executed whenever a user performs a query with the keyword. As advertisers may frequently change their bids, the game will have a large set of equilibria with potentially complex strategies. In this paper, we propose the use of natural strategies for reasoning in such setting as they are processable by artificial agents with limited memory and/or computational power as well as understandable by human users. To reach this goal, we introduce a quantitative version of Strategy Logic with natural strategies in the setting of imperfect information. In a first step, we show how to model strategies for repeated keyword auctions and take advantage of the model for proving properties evaluating this game. In a second step, we study the logic in relation to the distinguishing power, expressivity, and model-checking complexity for strategies with and without recall.

Extended Graded Modalities in Strategy Logic

Strategy Logic (SL) is a logical formalism for strategic reasoning in multi-agent systems. Its main feature is that it has variables for strategies that are associated to specific agents with a binding operator. We introduce Graded Strategy Logic (GradedSL), an extension of SL by graded quantifiers over tuples of strategy variables, i.e., "there exist at least g different tuples (x_1,...,x_n) of strategies" where g is a cardinal from the set N union {aleph_0, aleph_1, 2^aleph_0}. We prove that the model-checking problem of GradedSL is decidable. We then turn to the complexity of fragments of GradedSL. When the g's are restricted to finite cardinals, written GradedNSL, the complexity of model-checking is no harder than for SL, i.e., it is non-elementary in the quantifier rank. We illustrate our formalism by showing how to count the number of different strategy profiles that are Nash equilibria (NE), or subgame-perfect equilibria (SPE). By analyzing the structure of the specific formulas involved, we conclude that the important problems of checking for the existence of a unique NE or SPE can both be solved in 2ExpTime, which is not harder than merely checking for the existence of such equilibria.