LTLf+ and PPLTL+: Extending LTLf and PPLTL to Infinite Traces

We introduce LTLf+ and PPLTL+, two logics to express properties of infinite traces, that are based on the linear-time temporal logics LTLf and PPLTL on finite traces. LTLf+/PPLTL+ use levels of Manna and Pnueli's LTL safety-progress hierarchy, and thus have the same expressive power as LTL. However, they also retain a crucial characteristic of the reactive synthesis problem for the base logics: the game arena for strategy extraction can be derived from deterministic finite automata (DFA). Consequently, these logics circumvent the notorious difficulties associated with determinizing infinite trace automata, typical of LTL reactive synthesis. We present DFA-based synthesis techniques for LTLf+/PPLTL+, and show that synthesis is 2EXPTIME-complete for LTLf+ (matching LTLf) and EXPTIME-complete for PPLTL+ (matching PPLTL). Notably, while PPLTL+ retains the full expressive power of LTL, reactive synthesis is EXPTIME-complete instead of 2EXPTIME-complete. The techniques are also adapted to optimally solve satisfiability, validity, and model-checking, to get EXPSPACE-complete for LTLf+ (extending a recent result for the guarantee level using LTLf), and PSPACE-complete for PPLTL+.

LTLf Synthesis Under Environment Specifications for Reachability and Safety Properties

In this paper, we study LTLf synthesis under environment specifications for arbitrary reachability and safety properties. We consider both kinds of properties for both agent tasks and environment specifications, providing a complete landscape of synthesis algorithms. For each case, we devise a specific algorithm (optimal wrt complexity of the problem) and prove its correctness. The algorithms combine common building blocks in different ways. While some cases are already studied in literature others are studied here for the first time.

Stochastic Fairness and Language-Theoretic Fairness in Planning on Nondeterministic Domains

We address two central notions of fairness in the literature of planning on nondeterministic fully observable domains. The first, which we call stochastic fairness, is classical, and assumes an environment which operates probabilistically using possibly unknown probabilities. The second, which is language-theoretic, assumes that if an action is taken from a given state infinitely often then all its possible outcomes should appear infinitely often (we call this state-action fairness). While the two notions coincide for standard reachability goals, they diverge for temporally extended goals. This important difference has been overlooked in the planning literature, and we argue has led to confusion in a number of published algorithms which use reductions that were stated for state-action fairness, for which they are incorrect, while being correct for stochastic fairness. We remedy this and provide an optimal sound and complete algorithm for solving state-action fair planning for LTL/LTLf goals, as well as a correct proof of the lower bound of the goal-complexity (our proof is general enough that it provides new proofs also for the no-fairness and stochastic-fairness cases). Overall, we show that stochastic fairness is better behaved than state-action fairness.

Planning and Synthesis Under Assumptions

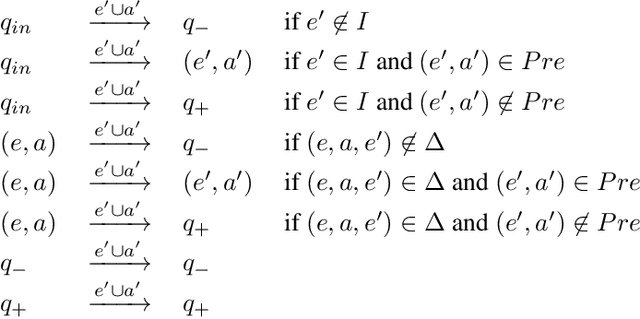
In Reasoning about Action and Planning, one synthesizes the agent plan by taking advantage of the assumption on how the environment works (that is, one exploits the environment's effects, its fairness, its trajectory constraints). In this paper we study this form of synthesis in detail. We consider assumptions as constraints on the possible strategies that the environment can have in order to respond to the agent's actions. Such constraints may be given in the form of a planning domain (or action theory), as linear-time formulas over infinite or finite runs, or as a combination of the two (e.g., FOND under fairness). We argue though that not all assumption specifications are meaningful: they need to be consistent, which means that there must exist an environment strategy fulfilling the assumption in spite of the agent actions. For such assumptions, we study how to do synthesis/planning for agent goals, ranging from a classical reachability to goal on traces specified in LTL and LTLf/LDLf, characterizing the problem both mathematically and algorithmically.

Extended Graded Modalities in Strategy Logic

Strategy Logic (SL) is a logical formalism for strategic reasoning in multi-agent systems. Its main feature is that it has variables for strategies that are associated to specific agents with a binding operator. We introduce Graded Strategy Logic (GradedSL), an extension of SL by graded quantifiers over tuples of strategy variables, i.e., "there exist at least g different tuples (x_1,...,x_n) of strategies" where g is a cardinal from the set N union {aleph_0, aleph_1, 2^aleph_0}. We prove that the model-checking problem of GradedSL is decidable. We then turn to the complexity of fragments of GradedSL. When the g's are restricted to finite cardinals, written GradedNSL, the complexity of model-checking is no harder than for SL, i.e., it is non-elementary in the quantifier rank. We illustrate our formalism by showing how to count the number of different strategy profiles that are Nash equilibria (NE), or subgame-perfect equilibria (SPE). By analyzing the structure of the specific formulas involved, we conclude that the important problems of checking for the existence of a unique NE or SPE can both be solved in 2ExpTime, which is not harder than merely checking for the existence of such equilibria.