Natural Strategic Ability in Stochastic Multi-Agent Systems

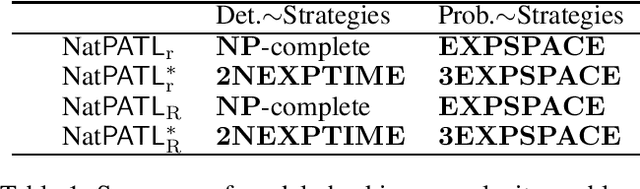
Strategies synthesized using formal methods can be complex and often require infinite memory, which does not correspond to the expected behavior when trying to model Multi-Agent Systems (MAS). To capture such behaviors, natural strategies are a recently proposed framework striking a balance between the ability of agents to strategize with memory and the model-checking complexity, but until now has been restricted to fully deterministic settings. For the first time, we consider the probabilistic temporal logics PATL and PATL* under natural strategies (NatPATL and NatPATL*, resp.). As main result we show that, in stochastic MAS, NatPATL model-checking is NP-complete when the active coalition is restricted to deterministic strategies. We also give a 2NEXPTIME complexity result for NatPATL* with the same restriction. In the unrestricted case, we give an EXPSPACE complexity for NatPATL and 3EXPSPACE complexity for NatPATL*.

Reasoning about Intuitionistic Computation Tree Logic

In this paper, we define an intuitionistic version of Computation Tree Logic. After explaining the semantic features of intuitionistic logic, we examine how these characteristics can be interesting for formal verification purposes. Subsequently, we define the syntax and semantics of our intuitionistic version of CTL and study some simple properties of the so obtained logic. We conclude by demonstrating that some fixed-point axioms of CTL are not valid in the intuitionistic version of CTL we have defined.

Discounting in Strategy Logic

Discounting is an important dimension in multi-agent systems as long as we want to reason about strategies and time. It is a key aspect in economics as it captures the intuition that the far-away future is not as important as the near future. Traditional verification techniques allow to check whether there is a winning strategy for a group of agents but they do not take into account the fact that satisfying a goal sooner is different from satisfying it after a long wait. In this paper, we augment Strategy Logic with future discounting over a set of discounted functions D, denoted SLdisc[D]. We consider "until" operators with discounting functions: the satisfaction value of a specification in SLdisc[D] is a value in [0, 1], where the longer it takes to fulfill requirements, the smaller the satisfaction value is. We motivate our approach with classical examples from Game Theory and study the complexity of model-checking SLdisc[D]-formulas.

Reasoning about Human-Friendly Strategies in Repeated Keyword Auctions

In online advertising, search engines sell ad placements for keywords continuously through auctions. This problem can be seen as an infinitely repeated game since the auction is executed whenever a user performs a query with the keyword. As advertisers may frequently change their bids, the game will have a large set of equilibria with potentially complex strategies. In this paper, we propose the use of natural strategies for reasoning in such setting as they are processable by artificial agents with limited memory and/or computational power as well as understandable by human users. To reach this goal, we introduce a quantitative version of Strategy Logic with natural strategies in the setting of imperfect information. In a first step, we show how to model strategies for repeated keyword auctions and take advantage of the model for proving properties evaluating this game. In a second step, we study the logic in relation to the distinguishing power, expressivity, and model-checking complexity for strategies with and without recall.

Equilibria for Games with Combined Qualitative and Quantitative Objectives

The overall aim of our research is to develop techniques to reason about the equilibrium properties of multi-agent systems. We model multi-agent systems as concurrent games, in which each player is a process that is assumed to act independently and strategically in pursuit of personal preferences. In this article, we study these games in the context of finite-memory strategies, and we assume players' preferences are defined by a qualitative and a quantitative objective, which are related by a lexicographic order: a player first prefers to satisfy its qualitative objective (given as a formula of Linear Temporal Logic) and then prefers to minimise costs (given by a mean-payoff function). Our main result is that deciding the existence of a strict epsilon Nash equilibrium in such games is 2ExpTime-complete (and hence decidable), even if players' deviations are implemented as infinite-memory strategies.

Dynamic Epistemic Logic Games with Epistemic Temporal Goals

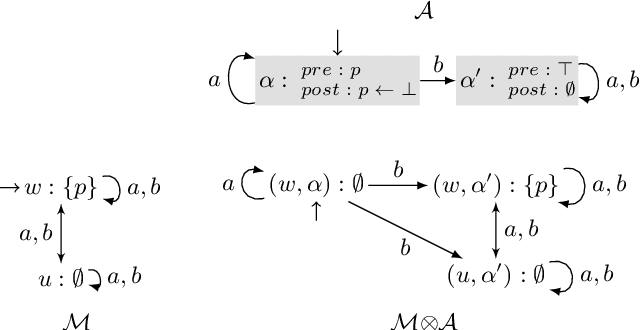
Dynamic Epistemic Logic (DEL) is a logical framework in which one can describe in great detail how actions are perceived by the agents, and how they affect the world. DEL games were recently introduced as a way to define classes of games with imperfect information where the actions available to the players are described very precisely. This framework makes it possible to define easily, for instance, classes of games where players can only use public actions or public announcements. These games have been studied for reachability objectives, where the aim is to reach a situation satisfying some epistemic property expressed in epistemic logic; several (un)decidability results have been established. In this work we show that the decidability results obtained for reachability objectives extend to a much more general class of winning conditions, namely those expressible in the epistemic temporal logic LTLK. To do so we establish that the infinite game structures generated by DEL public actions are regular, and we describe how to obtain finite representations on which we rely to solve them.

Changing Observations in Epistemic Temporal Logic

We study dynamic changes of agents' observational power in logics of knowledge and time. We consider CTL*K, the extension of CTL* with knowledge operators, and enrich it with a new operator that models a change in an agent's way of observing the system. We extend the classic semantics of knowledge for perfect-recall agents to account for changes of observation, and we show that this new operator strictly increases the expressivity of CTL*K. We reduce the model-checking problem for our logic to that for CTL*K, which is known to be decidable. This provides a solution to the model-checking problem for our logic, but its complexity is not optimal. Indeed we provide a direct decision procedure with better complexity.

Planning and Synthesis Under Assumptions

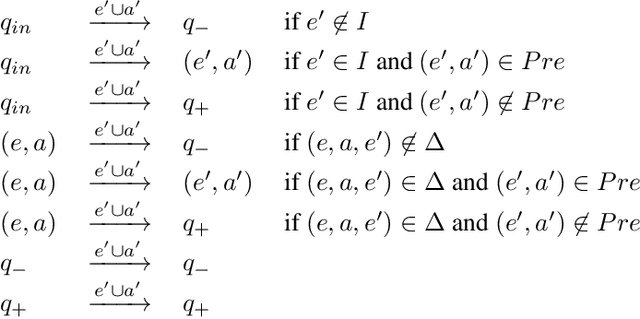
In Reasoning about Action and Planning, one synthesizes the agent plan by taking advantage of the assumption on how the environment works (that is, one exploits the environment's effects, its fairness, its trajectory constraints). In this paper we study this form of synthesis in detail. We consider assumptions as constraints on the possible strategies that the environment can have in order to respond to the agent's actions. Such constraints may be given in the form of a planning domain (or action theory), as linear-time formulas over infinite or finite runs, or as a combination of the two (e.g., FOND under fairness). We argue though that not all assumption specifications are meaningful: they need to be consistent, which means that there must exist an environment strategy fulfilling the assumption in spite of the agent actions. For such assumptions, we study how to do synthesis/planning for agent goals, ranging from a classical reachability to goal on traces specified in LTL and LTLf/LDLf, characterizing the problem both mathematically and algorithmically.

Extended Graded Modalities in Strategy Logic

Strategy Logic (SL) is a logical formalism for strategic reasoning in multi-agent systems. Its main feature is that it has variables for strategies that are associated to specific agents with a binding operator. We introduce Graded Strategy Logic (GradedSL), an extension of SL by graded quantifiers over tuples of strategy variables, i.e., "there exist at least g different tuples (x_1,...,x_n) of strategies" where g is a cardinal from the set N union {aleph_0, aleph_1, 2^aleph_0}. We prove that the model-checking problem of GradedSL is decidable. We then turn to the complexity of fragments of GradedSL. When the g's are restricted to finite cardinals, written GradedNSL, the complexity of model-checking is no harder than for SL, i.e., it is non-elementary in the quantifier rank. We illustrate our formalism by showing how to count the number of different strategy profiles that are Nash equilibria (NE), or subgame-perfect equilibria (SPE). By analyzing the structure of the specific formulas involved, we conclude that the important problems of checking for the existence of a unique NE or SPE can both be solved in 2ExpTime, which is not harder than merely checking for the existence of such equilibria.

The Complexity of Enriched Mu-Calculi

The fully enriched μ-calculus is the extension of the propositional μ-calculus with inverse programs, graded modalities, and nominals. While satisfiability in several expressive fragments of the fully enriched μ-calculus is known to be decidable and ExpTime-complete, it has recently been proved that the full calculus is undecidable. In this paper, we study the fragments of the fully enriched μ-calculus that are obtained by dropping at least one of the additional constructs. We show that, in all fragments obtained in this way, satisfiability is decidable and ExpTime-complete. Thus, we identify a family of decidable logics that are maximal (and incomparable) in expressive power. Our results are obtained by introducing two new automata models, showing that their emptiness problems are ExpTime-complete, and then reducing satisfiability in the relevant logics to these problems. The automata models we introduce are two-way graded alternating parity automata over infinite trees (2GAPTs) and fully enriched automata (FEAs) over infinite forests. The former are a common generalization of two incomparable automata models from the literature. The latter extend alternating automata in a similar way as the fully enriched μ-calculus extends the standard μ-calculus.