Natural Strategic Ability in Stochastic Multi-Agent Systems

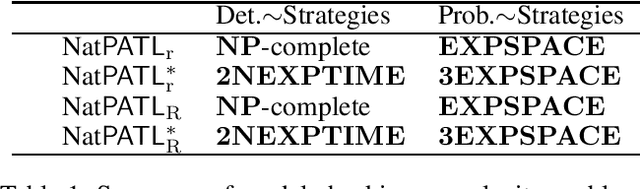
Strategies synthesized using formal methods can be complex and often require infinite memory, which does not correspond to the expected behavior when trying to model Multi-Agent Systems (MAS). To capture such behaviors, natural strategies are a recently proposed framework striking a balance between the ability of agents to strategize with memory and the model-checking complexity, but until now has been restricted to fully deterministic settings. For the first time, we consider the probabilistic temporal logics PATL and PATL* under natural strategies (NatPATL and NatPATL*, resp.). As main result we show that, in stochastic MAS, NatPATL model-checking is NP-complete when the active coalition is restricted to deterministic strategies. We also give a 2NEXPTIME complexity result for NatPATL* with the same restriction. In the unrestricted case, we give an EXPSPACE complexity for NatPATL and 3EXPSPACE complexity for NatPATL*.

Active Learning of Sequential Transducers with Side Information about the Domain

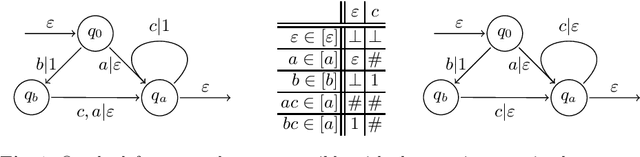
Active learning is a setting in which a student queries a teacher, through membership and equivalence queries, in order to learn a language. Performance on these algorithms is often measured in the number of queries required to learn a target, with an emphasis on costly equivalence queries. In graybox learning, the learning process is accelerated by foreknowledge of some information on the target. Here, we consider graybox active learning of subsequential string transducers, where a regular overapproximation of the domain is known by the student. We show that there exists an algorithm using string equation solvers that uses this knowledge to learn subsequential string transducers with a better guarantee on the required number of equivalence queries than classical active learning.

Mixing Probabilistic and non-Probabilistic Objectives in Markov Decision Processes

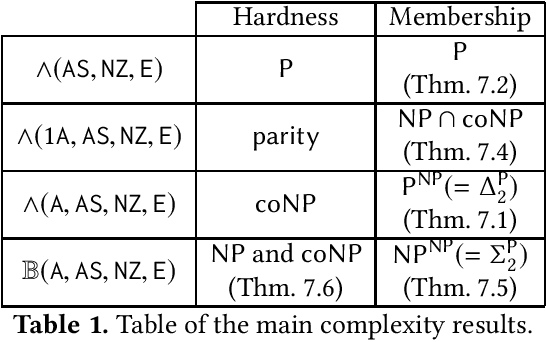
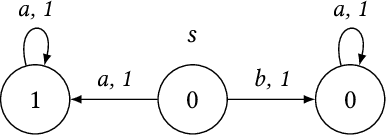
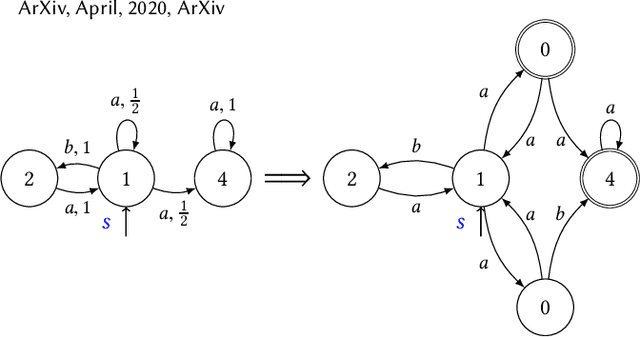
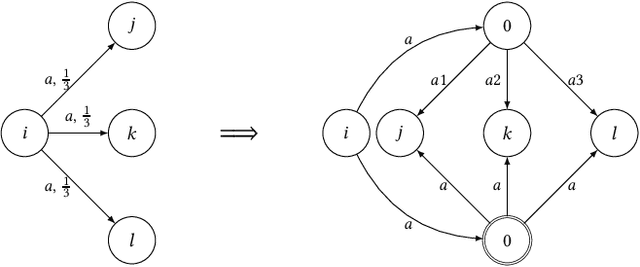
In this paper, we consider algorithms to decide the existence of strategies in MDPs for Boolean combinations of objectives. These objectives are omega-regular properties that need to be enforced either surely, almost surely, existentially, or with non-zero probability. In this setting, relevant strategies are randomized infinite memory strategies: both infinite memory and randomization may be needed to play optimally. We provide algorithms to solve the general case of Boolean combinations and we also investigate relevant subcases. We further report on complexity bounds for these problems.

Threshold Constraints with Guarantees for Parity Objectives in Markov Decision Processes

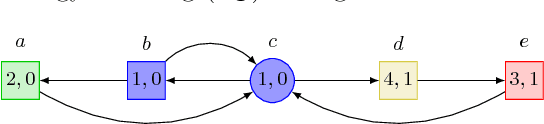
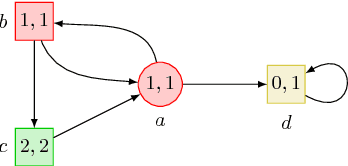
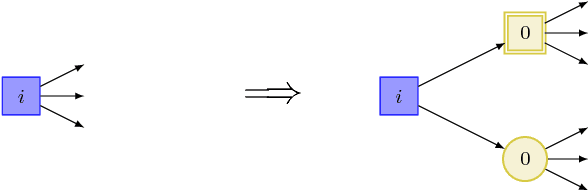
The beyond worst-case synthesis problem was introduced recently by Bruy\`ere et al. [BFRR14]: it aims at building system controllers that provide strict worst-case performance guarantees against an antagonistic environment while ensuring higher expected performance against a stochastic model of the environment. Our work extends the framework of [BFRR14] and follow-up papers, which focused on quantitative objectives, by addressing the case of $\omega$-regular conditions encoded as parity objectives, a natural way to represent functional requirements of systems. We build strategies that satisfy a main parity objective on all plays, while ensuring a secondary one with sufficient probability. This setting raises new challenges in comparison to quantitative objectives, as one cannot easily mix different strategies without endangering the functional properties of the system. We establish that, for all variants of this problem, deciding the existence of a strategy lies in ${\sf NP} \cap {\sf coNP}$, the same complexity class as classical parity games. Hence, our framework provides additional modeling power while staying in the same complexity class. [BFRR14] V\'eronique Bruy\`ere, Emmanuel Filiot, Mickael Randour, and Jean-Fran\c{c}ois Raskin. Meet your expectations with guarantees: Beyond worst-case synthesis in quantitative games. In Ernst W. Mayr and Natacha Portier, editors, 31st International Symposium on Theoretical Aspects of Computer Science, STACS 2014, March 5-8, 2014, Lyon, France, volume 25 of LIPIcs, pages 199-213. Schloss Dagstuhl - Leibniz - Zentrum fuer Informatik, 2014.