Mixing Probabilistic and non-Probabilistic Objectives in Markov Decision Processes
Paper and Code
Apr 28, 2020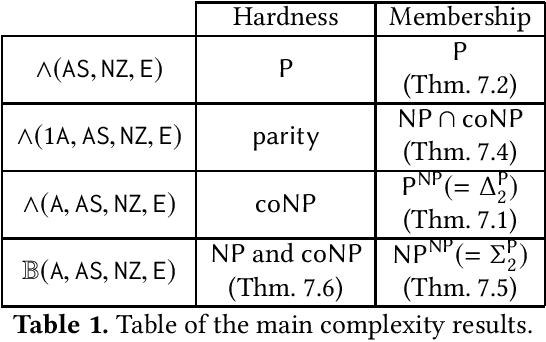
In this paper, we consider algorithms to decide the existence of strategies in MDPs for Boolean combinations of objectives. These objectives are omega-regular properties that need to be enforced either surely, almost surely, existentially, or with non-zero probability. In this setting, relevant strategies are randomized infinite memory strategies: both infinite memory and randomization may be needed to play optimally. We provide algorithms to solve the general case of Boolean combinations and we also investigate relevant subcases. We further report on complexity bounds for these problems.
* Paper accepted to LICS 2020 - Full version
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge