François Schwarzentruber
Verifying Graph Neural Networks with Readout is Intractable
Oct 09, 2025



Abstract:We introduce a logical language for reasoning about quantized aggregate-combine graph neural networks with global readout (ACR-GNNs). We provide a logical characterization and use it to prove that verification tasks for quantized GNNs with readout are (co)NEXPTIME-complete. This result implies that the verification of quantized GNNs is computationally intractable, prompting substantial research efforts toward ensuring the safety of GNN-based systems. We also experimentally demonstrate that quantized ACR-GNN models are lightweight while maintaining good accuracy and generalization capabilities with respect to non-quantized models.
Verifying Quantized Graph Neural Networks is PSPACE-complete
Feb 22, 2025



Abstract:In this paper, we investigate verification of quantized Graph Neural Networks (GNNs), where some fixed-width arithmetic is used to represent numbers. We introduce the linear-constrained validity (LVP) problem for verifying GNNs properties, and provide an efficient translation from LVP instances into a logical language. We show that LVP is in PSPACE, for any reasonable activation functions. We provide a proof system. We also prove PSPACE-hardness, indicating that while reasoning about quantized GNNs is feasible, it remains generally computationally challenging.
A Computationally Grounded Framework for Cognitive Attitudes (extended version)
Dec 18, 2024


Abstract:We introduce a novel language for reasoning about agents' cognitive attitudes of both epistemic and motivational type. We interpret it by means of a computationally grounded semantics using belief bases. Our language includes five types of modal operators for implicit belief, complete attraction, complete repulsion, realistic attraction and realistic repulsion. We give an axiomatization and show that our operators are not mutually expressible and that they can be combined to represent a large variety of psychological concepts including ambivalence, indifference, being motivated, being demotivated and preference. We present a dynamic extension of the language that supports reasoning about the effects of belief change operations. Finally, we provide a succinct formulation of model checking for our languages and a PSPACE model checking algorithm relying on a reduction into TQBF. We present some experimental results for the implemented algorithm on computation time in a concrete example.
A Logic for Reasoning About Aggregate-Combine Graph Neural Networks
Apr 30, 2024
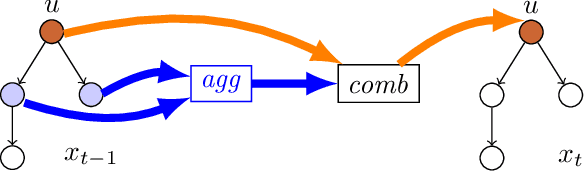

Abstract:We propose a modal logic in which counting modalities appear in linear inequalities. We show that each formula can be transformed into an equivalent graph neural network (GNN). We also show that a broad class of GNNs can be transformed efficiently into a formula, thus significantly improving upon the literature about the logical expressiveness of GNNs. We also show that the satisfiability problem is PSPACE-complete. These results bring together the promise of using standard logical methods for reasoning about GNNs and their properties, particularly in applications such as GNN querying, equivalence checking, etc. We prove that such natural problems can be solved in polynomial space.
Base-based Model Checking for Multi-Agent Only Believing
Jul 27, 2023
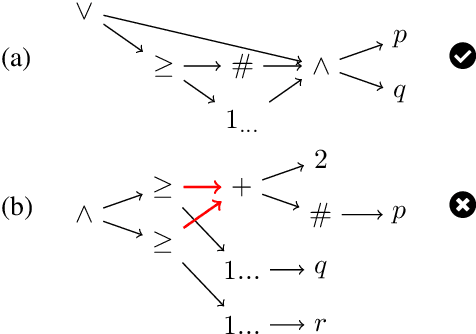
Abstract:We present a novel semantics for the language of multi-agent only believing exploiting belief bases, and show how to use it for automatically checking formulas of this language and of its dynamic extension with private belief expansion operators. We provide a PSPACE algorithm for model checking relying on a reduction to QBF and alternative dedicated algorithm relying on the exploration of the state space. We present an implementation of the QBF-based algorithm and some experimental results on computation time in a concrete example.
A Modal Logic for Explaining some Graph Neural Networks
Jul 11, 2023



Abstract:In this paper, we propose a modal logic in which counting modalities appear in linear inequalities. We show that each formula can be transformed into an equivalent graph neural network (GNN). We also show that each GNN can be transformed into a formula. We show that the satisfiability problem is decidable. We also discuss some variants that are in PSPACE.
On simple expectations and observations of intelligent agents: A complexity study
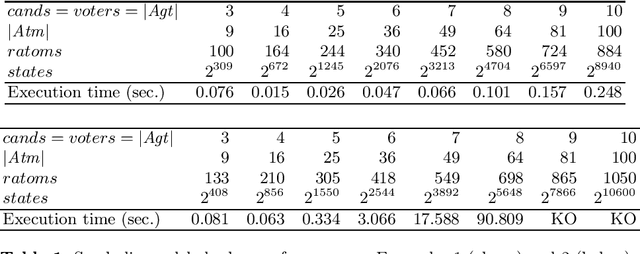
Jun 05, 2023

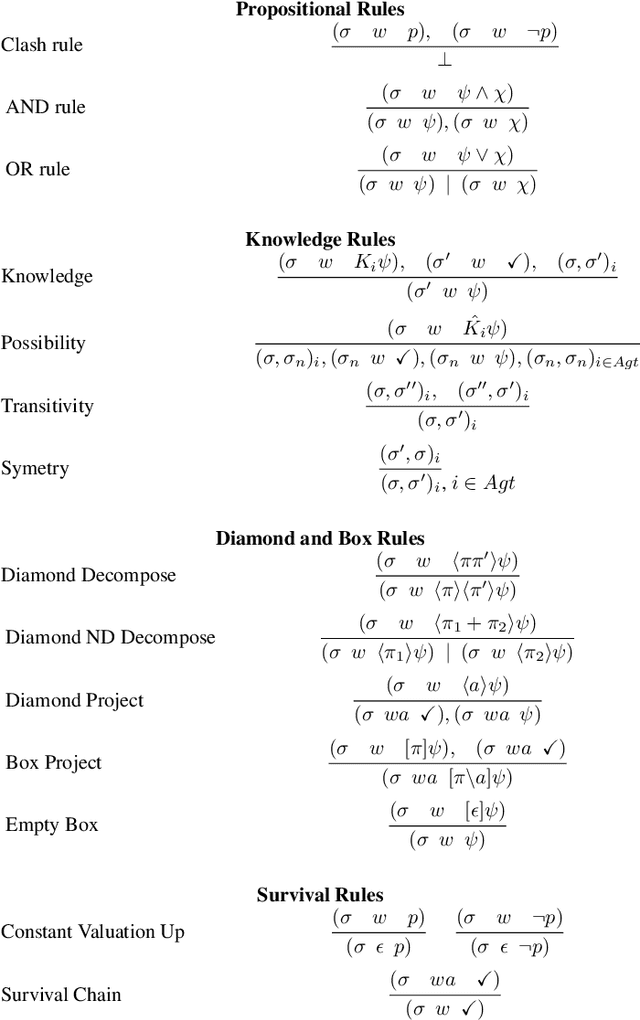
Abstract:Public observation logic (POL) reasons about agent expectations and agent observations in various real world situations. The expectations of agents take shape based on certain protocols about the world around and they remove those possible scenarios where their expectations and observations do not match. This in turn influences the epistemic reasoning of these agents. In this work, we study the computational complexity of the satisfaction problems of various fragments of POL. In the process, we also highlight the inevitable link that these fragments have with the well-studied Public announcement logic.
On verifying expectations and observations of intelligent agents
May 12, 2022

Abstract:Public observation logic (POL) is a variant of dynamic epistemic logic to reason about agent expectations and agent observations. Agents have certain expectations, regarding the situation at hand, that are actuated by the relevant protocols, and they eliminate possible worlds in which their expectations do not match with their observations. In this work, we investigate the computational complexity of the model checking problem for POL and prove its PSPACE-completeness. We also study various syntactic fragments of POL. We exemplify the applicability of POL model checking in verifying different characteristics and features of an interactive system with respect to the distinct expectations and (matching) observations of the system. Finally, we provide a discussion on the implementation of the model checking algorithms.
Conflict-Based Search for Connected Multi-Agent Path Finding
Jun 05, 2020



Abstract:We study a variant of the multi-agent path finding problem (MAPF) in which agents are required to remain connected to each other and to a designated base. This problem has applications in search and rescue missions where the entire execution must be monitored by a human operator. We re-visit the conflict-based search algorithm known for MAPF, and define a variant where conflicts arise from disconnections rather than collisions. We study optimizations, and give experimental results in which we compare our algorithms with the literature.
Dynamic Epistemic Logic Games with Epistemic Temporal Goals
Jan 20, 2020
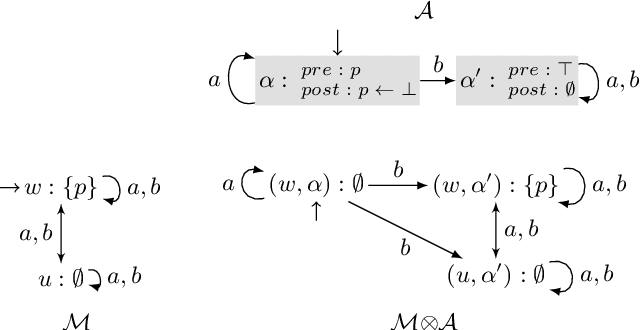
Abstract:Dynamic Epistemic Logic (DEL) is a logical framework in which one can describe in great detail how actions are perceived by the agents, and how they affect the world. DEL games were recently introduced as a way to define classes of games with imperfect information where the actions available to the players are described very precisely. This framework makes it possible to define easily, for instance, classes of games where players can only use public actions or public announcements. These games have been studied for reachability objectives, where the aim is to reach a situation satisfying some epistemic property expressed in epistemic logic; several (un)decidability results have been established. In this work we show that the decidability results obtained for reachability objectives extend to a much more general class of winning conditions, namely those expressible in the epistemic temporal logic LTLK. To do so we establish that the infinite game structures generated by DEL public actions are regular, and we describe how to obtain finite representations on which we rely to solve them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge