A Computationally Grounded Framework for Cognitive Attitudes (extended version)

We introduce a novel language for reasoning about agents' cognitive attitudes of both epistemic and motivational type. We interpret it by means of a computationally grounded semantics using belief bases. Our language includes five types of modal operators for implicit belief, complete attraction, complete repulsion, realistic attraction and realistic repulsion. We give an axiomatization and show that our operators are not mutually expressible and that they can be combined to represent a large variety of psychological concepts including ambivalence, indifference, being motivated, being demotivated and preference. We present a dynamic extension of the language that supports reasoning about the effects of belief change operations. Finally, we provide a succinct formulation of model checking for our languages and a PSPACE model checking algorithm relying on a reduction into TQBF. We present some experimental results for the implemented algorithm on computation time in a concrete example.

Base-based Model Checking for Multi-Agent Only Believing

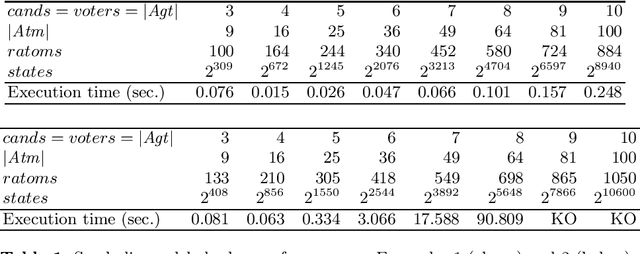
We present a novel semantics for the language of multi-agent only believing exploiting belief bases, and show how to use it for automatically checking formulas of this language and of its dynamic extension with private belief expansion operators. We provide a PSPACE algorithm for model checking relying on a reduction to QBF and alternative dedicated algorithm relying on the exploration of the state space. We present an implementation of the QBF-based algorithm and some experimental results on computation time in a concrete example.

Tableaux for Dynamic Logic of Propositional Assignments

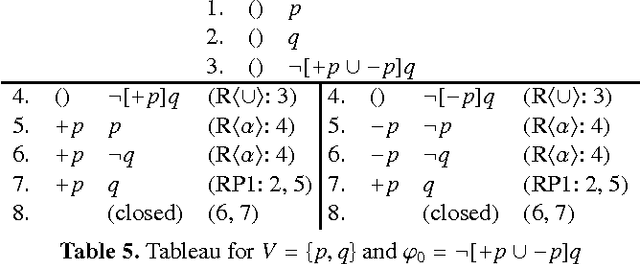
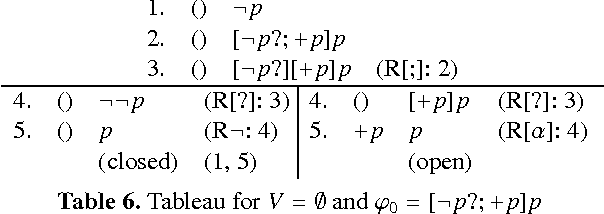
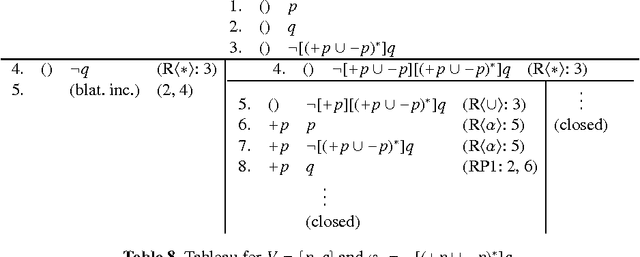
The Dynamic Logic for Propositional Assignments (DL-PA) has recently been studied as an alternative to Propositional Dynamic Logic (PDL). In DL-PA, the abstract atomic programs of PDL are replaced by assignments of propositional variables to truth values. This makes DL-PA enjoy some interesting meta-logical properties that PDL does not, such as eliminability of the Kleene star, compactness and interpolation. We define and analytic tableaux calculus for DL-PA and show that it matches the known complexity results.