A Logic for Reasoning About Aggregate-Combine Graph Neural Networks

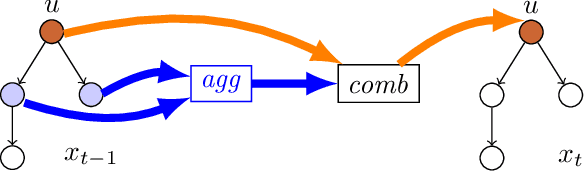
We propose a modal logic in which counting modalities appear in linear inequalities. We show that each formula can be transformed into an equivalent graph neural network (GNN). We also show that a broad class of GNNs can be transformed efficiently into a formula, thus significantly improving upon the literature about the logical expressiveness of GNNs. We also show that the satisfiability problem is PSPACE-complete. These results bring together the promise of using standard logical methods for reasoning about GNNs and their properties, particularly in applications such as GNN querying, equivalence checking, etc. We prove that such natural problems can be solved in polynomial space.

A Modal Logic for Explaining some Graph Neural Networks

In this paper, we propose a modal logic in which counting modalities appear in linear inequalities. We show that each formula can be transformed into an equivalent graph neural network (GNN). We also show that each GNN can be transformed into a formula. We show that the satisfiability problem is decidable. We also discuss some variants that are in PSPACE.