A Logic for Reasoning About Aggregate-Combine Graph Neural Networks

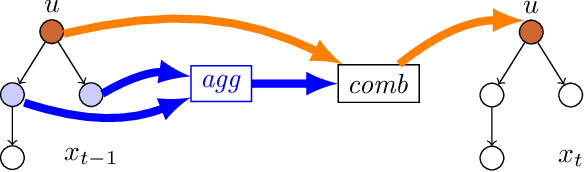
We propose a modal logic in which counting modalities appear in linear inequalities. We show that each formula can be transformed into an equivalent graph neural network (GNN). We also show that a broad class of GNNs can be transformed efficiently into a formula, thus significantly improving upon the literature about the logical expressiveness of GNNs. We also show that the satisfiability problem is PSPACE-complete. These results bring together the promise of using standard logical methods for reasoning about GNNs and their properties, particularly in applications such as GNN querying, equivalence checking, etc. We prove that such natural problems can be solved in polynomial space.

Social, Legal, Ethical, Empathetic, and Cultural Rules: Compilation and Reasoning (Extended Version)

The rise of AI-based and autonomous systems is raising concerns and apprehension due to potential negative repercussions stemming from their behavior or decisions. These systems must be designed to comply with the human contexts in which they will operate. To this extent, Townsend et al. (2022) introduce the concept of SLEEC (social, legal, ethical, empathetic, or cultural) rules that aim to facilitate the formulation, verification, and enforcement of the rules AI-based and autonomous systems should obey. They lay out a methodology to elicit them and to let philosophers, lawyers, domain experts, and others to formulate them in natural language. To enable their effective use in AI systems, it is necessary to translate these rules systematically into a formal language that supports automated reasoning. In this study, we first conduct a linguistic analysis of the SLEEC rules pattern, which justifies the translation of SLEEC rules into classical logic. Then we investigate the computational complexity of reasoning about SLEEC rules and show how logical programming frameworks can be employed to implement SLEEC rules in practical scenarios. The result is a readily applicable strategy for implementing AI systems that conform to norms expressed as SLEEC rules.

A Semantic Approach to Decidability in Epistemic Planning (Extended Version)

The use of Dynamic Epistemic Logic (DEL) in multi-agent planning has led to a widely adopted action formalism that can handle nondeterminism, partial observability and arbitrary knowledge nesting. As such expressive power comes at the cost of undecidability, several decidable fragments have been isolated, mainly based on syntactic restrictions of the action formalism. In this paper, we pursue a novel semantic approach to achieve decidability. Namely, rather than imposing syntactical constraints, the semantic approach focuses on the axioms of the logic for epistemic planning. Specifically, we augment the logic of knowledge S5$_n$ and with an interaction axiom called (knowledge) commutativity, which controls the ability of agents to unboundedly reason on the knowledge of other agents. We then provide a threefold contribution. First, we show that the resulting epistemic planning problem is decidable. In doing so, we prove that our framework admits a finitary non-fixpoint characterization of common knowledge, which is of independent interest. Second, we study different generalizations of the commutativity axiom, with the goal of obtaining decidability for more expressive fragments of DEL. Finally, we show that two well-known epistemic planning systems based on action templates, when interpreted under the setting of knowledge, conform to the commutativity axiom, hence proving their decidability.

Learning Ontologies with Epistemic Reasoning: The EL Case

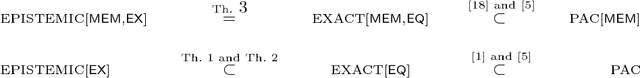
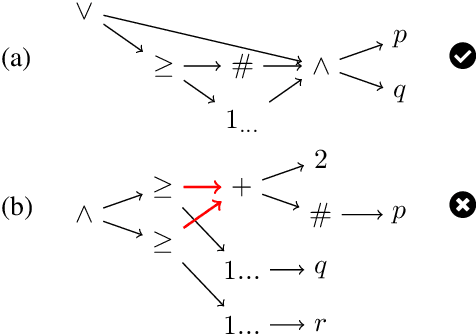
We investigate the problem of learning description logic ontologies from entailments via queries, using epistemic reasoning. We introduce a new learning model consisting of epistemic membership and example queries and show that polynomial learnability in this model coincides with polynomial learnability in Angluin's exact learning model with membership and equivalence queries. We then instantiate our learning framework to EL and show some complexity results for an epistemic extension of EL where epistemic operators can be applied over the axioms. Finally, we transfer known results for EL ontologies and its fragments to our learning model based on epistemic reasoning.

Repairing Ontologies via Axiom Weakening

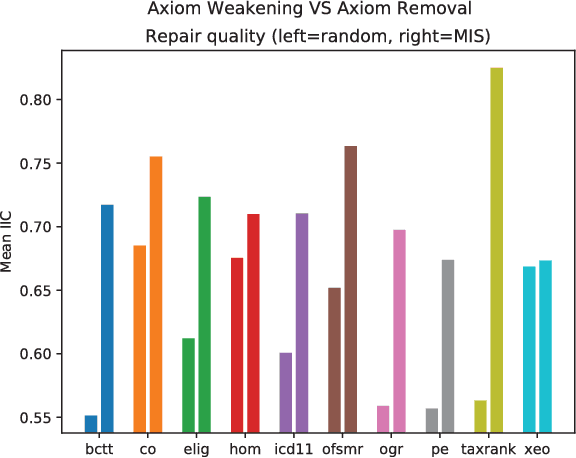
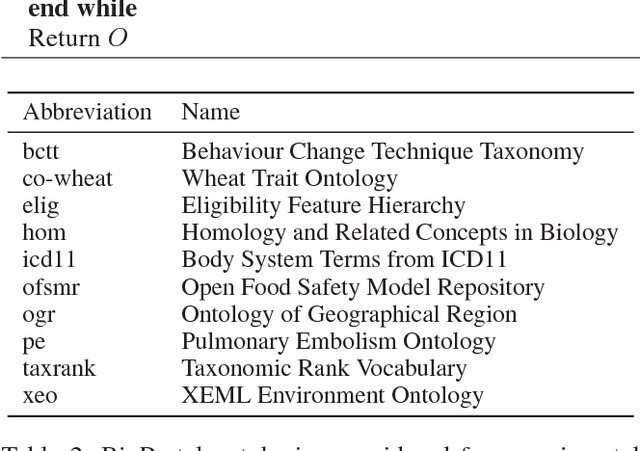
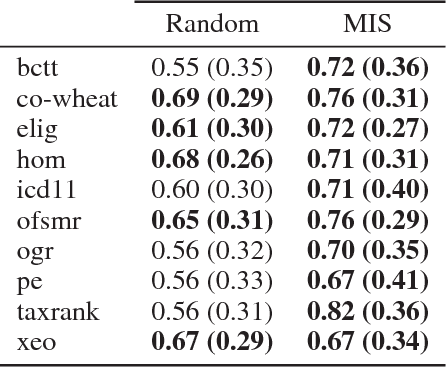
Ontology engineering is a hard and error-prone task, in which small changes may lead to errors, or even produce an inconsistent ontology. As ontologies grow in size, the need for automated methods for repairing inconsistencies while preserving as much of the original knowledge as possible increases. Most previous approaches to this task are based on removing a few axioms from the ontology to regain consistency. We propose a new method based on weakening these axioms to make them less restrictive, employing the use of refinement operators. We introduce the theoretical framework for weakening DL ontologies, propose algorithms to repair ontologies based on the framework, and provide an analysis of the computational complexity. Through an empirical analysis made over real-life ontologies, we show that our approach preserves significantly more of the original knowledge of the ontology than removing axioms.

Non-normal modalities in variants of Linear Logic

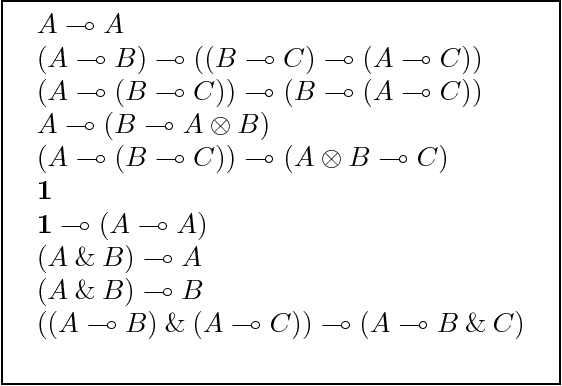
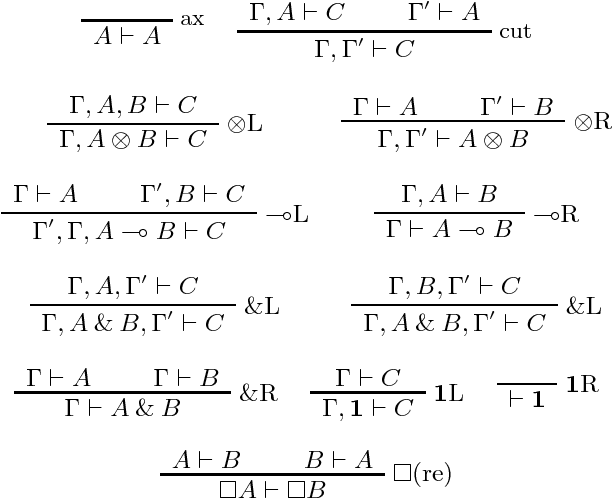
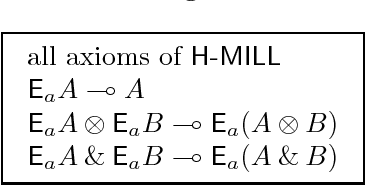
This article presents modal versions of resource-conscious logics. We concentrate on extensions of variants of Linear Logic with one minimal non-normal modality. In earlier work, where we investigated agency in multi-agent systems, we have shown that the results scale up to logics with multiple non-minimal modalities. Here, we start with the language of propositional intuitionistic Linear Logic without the additive disjunction, to which we add a modality. We provide an interpretation of this language on a class of Kripke resource models extended with a neighbourhood function: modal Kripke resource models. We propose a Hilbert-style axiomatization and a Gentzen-style sequent calculus. We show that the proof theories are sound and complete with respect to the class of modal Kripke resource models. We show that the sequent calculus admits cut elimination and that proof-search is in PSPACE. We then show how to extend the results when non-commutative connectives are added to the language. Finally, we put the logical framework to use by instantiating it as logics of agency. In particular, we propose a logic to reason about the resource-sensitive use of artefacts and illustrate it with a variety of examples.