Non-normal modalities in variants of Linear Logic
Paper and Code
Sep 04, 2015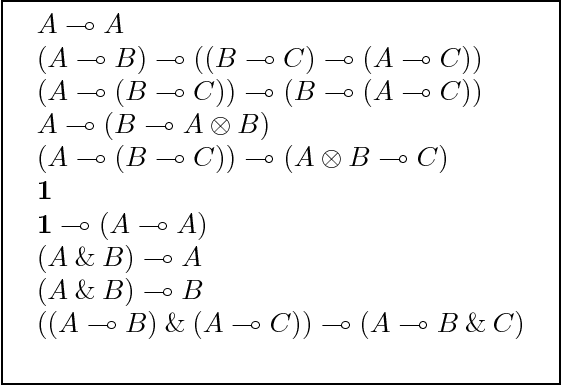
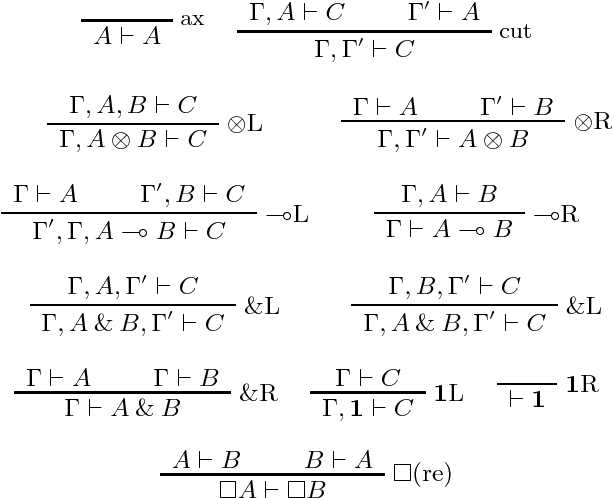

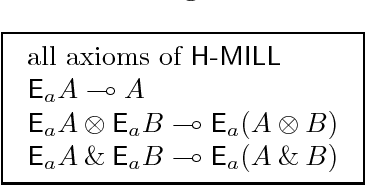
This article presents modal versions of resource-conscious logics. We concentrate on extensions of variants of Linear Logic with one minimal non-normal modality. In earlier work, where we investigated agency in multi-agent systems, we have shown that the results scale up to logics with multiple non-minimal modalities. Here, we start with the language of propositional intuitionistic Linear Logic without the additive disjunction, to which we add a modality. We provide an interpretation of this language on a class of Kripke resource models extended with a neighbourhood function: modal Kripke resource models. We propose a Hilbert-style axiomatization and a Gentzen-style sequent calculus. We show that the proof theories are sound and complete with respect to the class of modal Kripke resource models. We show that the sequent calculus admits cut elimination and that proof-search is in PSPACE. We then show how to extend the results when non-commutative connectives are added to the language. Finally, we put the logical framework to use by instantiating it as logics of agency. In particular, we propose a logic to reason about the resource-sensitive use of artefacts and illustrate it with a variety of examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge