DOLCE: A Descriptive Ontology for Linguistic and Cognitive Engineering

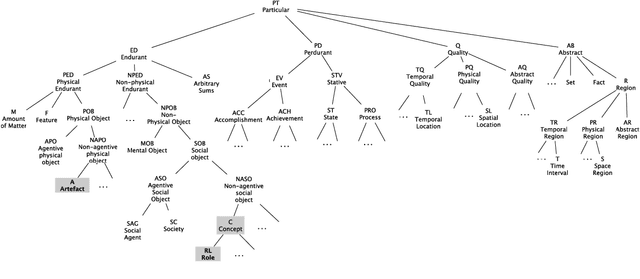
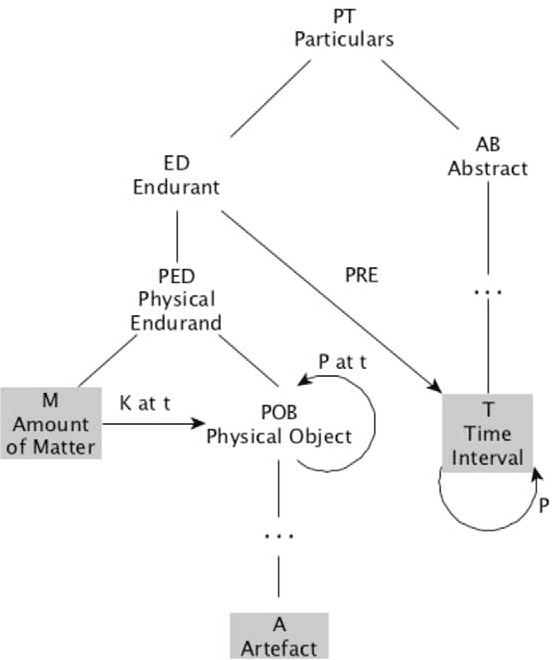
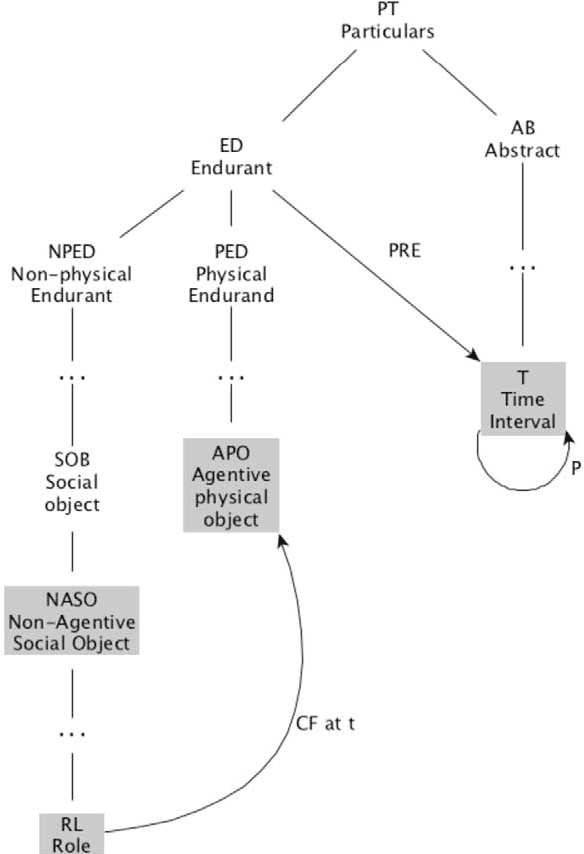
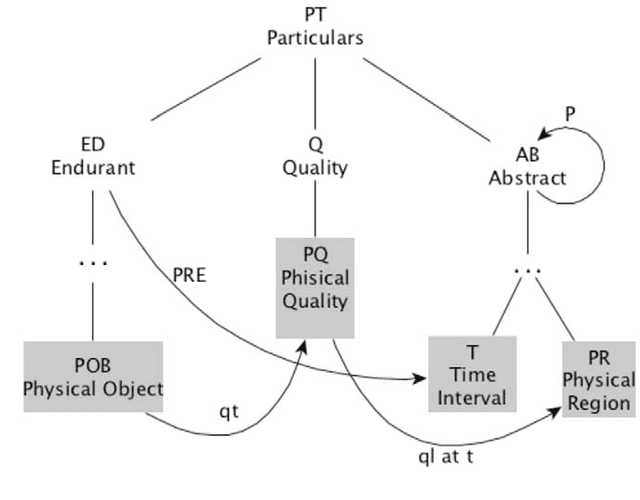
DOLCE, the first top-level (foundational) ontology to be axiomatized, has remained stable for twenty years and today is broadly used in a variety of domains. DOLCE is inspired by cognitive and linguistic considerations and aims to model a commonsense view of reality, like the one human beings exploit in everyday life in areas as diverse as socio-technical systems, manufacturing, financial transactions and cultural heritage. DOLCE clearly lists the ontological choices it is based upon, relies on philosophical principles, is richly formalized, and is built according to well-established ontological methodologies, e.g. OntoClean. Because of these features, it has inspired most of the existing top-level ontologies and has been used to develop or improve standards and public domain resources (e.g. CIDOC CRM, DBpedia and WordNet). Being a foundational ontology, DOLCE is not directly concerned with domain knowledge. Its purpose is to provide the general categories and relations needed to give a coherent view of reality, to integrate domain knowledge, and to mediate across domains. In these 20 years DOLCE has shown that applied ontologies can be stable and that interoperability across reference and domain ontologies is a reality. This paper briefly introduces the ontology and shows how to use it on a few modeling cases.

Repairing Ontologies via Axiom Weakening

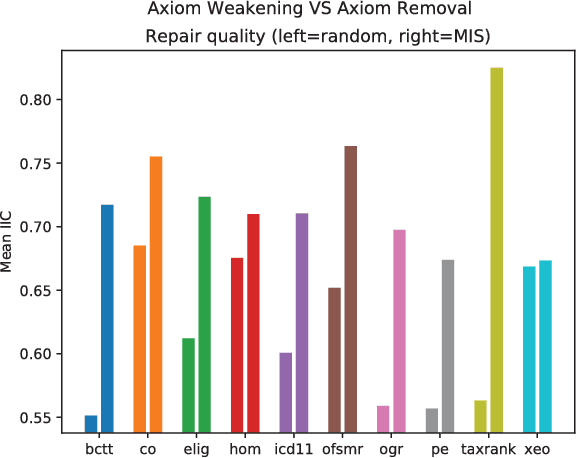
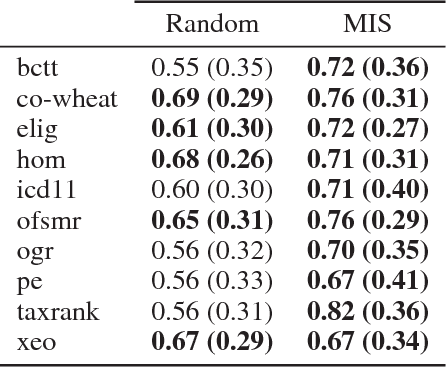
Ontology engineering is a hard and error-prone task, in which small changes may lead to errors, or even produce an inconsistent ontology. As ontologies grow in size, the need for automated methods for repairing inconsistencies while preserving as much of the original knowledge as possible increases. Most previous approaches to this task are based on removing a few axioms from the ontology to regain consistency. We propose a new method based on weakening these axioms to make them less restrictive, employing the use of refinement operators. We introduce the theoretical framework for weakening DL ontologies, propose algorithms to repair ontologies based on the framework, and provide an analysis of the computational complexity. Through an empirical analysis made over real-life ontologies, we show that our approach preserves significantly more of the original knowledge of the ontology than removing axioms.

Non-normal modalities in variants of Linear Logic

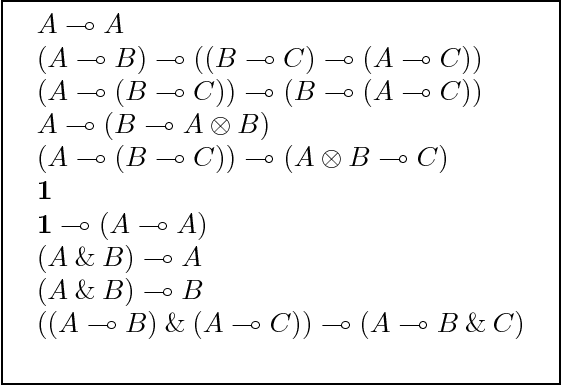
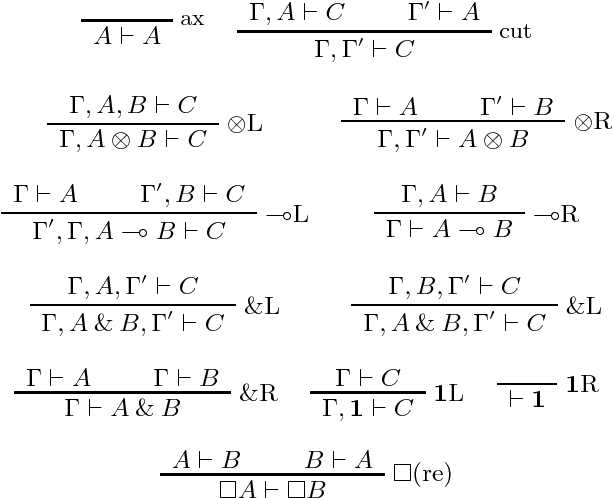
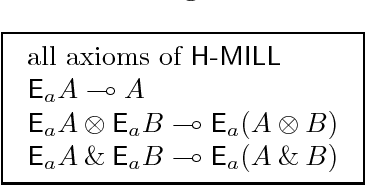
This article presents modal versions of resource-conscious logics. We concentrate on extensions of variants of Linear Logic with one minimal non-normal modality. In earlier work, where we investigated agency in multi-agent systems, we have shown that the results scale up to logics with multiple non-minimal modalities. Here, we start with the language of propositional intuitionistic Linear Logic without the additive disjunction, to which we add a modality. We provide an interpretation of this language on a class of Kripke resource models extended with a neighbourhood function: modal Kripke resource models. We propose a Hilbert-style axiomatization and a Gentzen-style sequent calculus. We show that the proof theories are sound and complete with respect to the class of modal Kripke resource models. We show that the sequent calculus admits cut elimination and that proof-search is in PSPACE. We then show how to extend the results when non-commutative connectives are added to the language. Finally, we put the logical framework to use by instantiating it as logics of agency. In particular, we propose a logic to reason about the resource-sensitive use of artefacts and illustrate it with a variety of examples.