Repairing Ontologies via Axiom Weakening

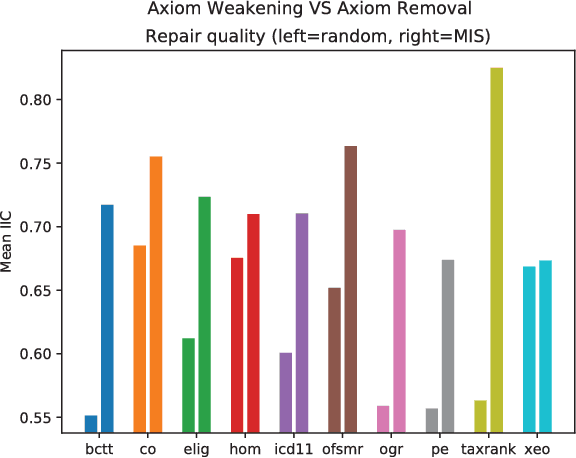
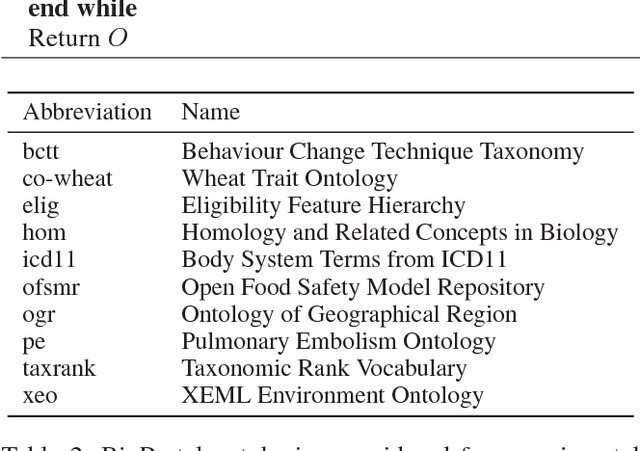
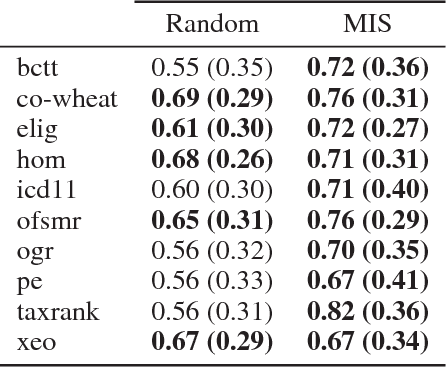
Ontology engineering is a hard and error-prone task, in which small changes may lead to errors, or even produce an inconsistent ontology. As ontologies grow in size, the need for automated methods for repairing inconsistencies while preserving as much of the original knowledge as possible increases. Most previous approaches to this task are based on removing a few axioms from the ontology to regain consistency. We propose a new method based on weakening these axioms to make them less restrictive, employing the use of refinement operators. We introduce the theoretical framework for weakening DL ontologies, propose algorithms to repair ontologies based on the framework, and provide an analysis of the computational complexity. Through an empirical analysis made over real-life ontologies, we show that our approach preserves significantly more of the original knowledge of the ontology than removing axioms.

Gray-box inference for structured Gaussian process models

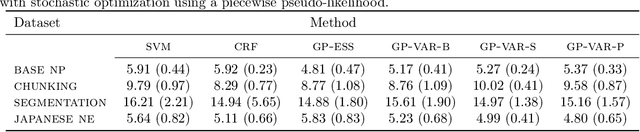
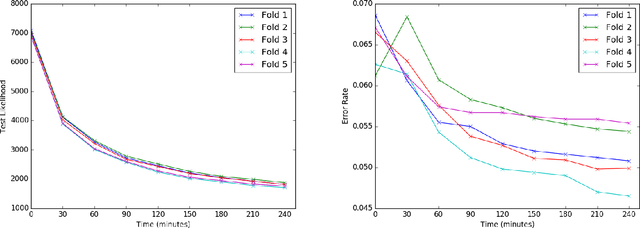
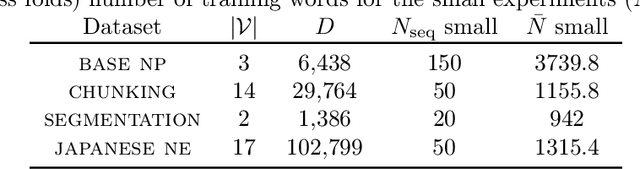
We develop an automated variational inference method for Bayesian structured prediction problems with Gaussian process (GP) priors and linear-chain likelihoods. Our approach does not need to know the details of the structured likelihood model and can scale up to a large number of observations. Furthermore, we show that the required expected likelihood term and its gradients in the variational objective (ELBO) can be estimated efficiently by using expectations over very low-dimensional Gaussian distributions. Optimization of the ELBO is fully parallelizable over sequences and amenable to stochastic optimization, which we use along with control variate techniques and state-of-the-art incremental optimization to make our framework useful in practice. Results on a set of natural language processing tasks show that our method can be as good as (and sometimes better than) hard-coded approaches including SVM-struct and CRFs, and overcomes the scalability limitations of previous inference algorithms based on sampling. Overall, this is a fundamental step to developing automated inference methods for Bayesian structured prediction.

The Doxastic Interpretation of Team Semantics

We advance a doxastic interpretation for many of the logical connectives considered in Dependence Logic and in its extensions, and we argue that Team Semantics is a natural framework for reasoning about beliefs and belief updates.