Enriching Ontology-based Data Access with Provenance (Extended Version)

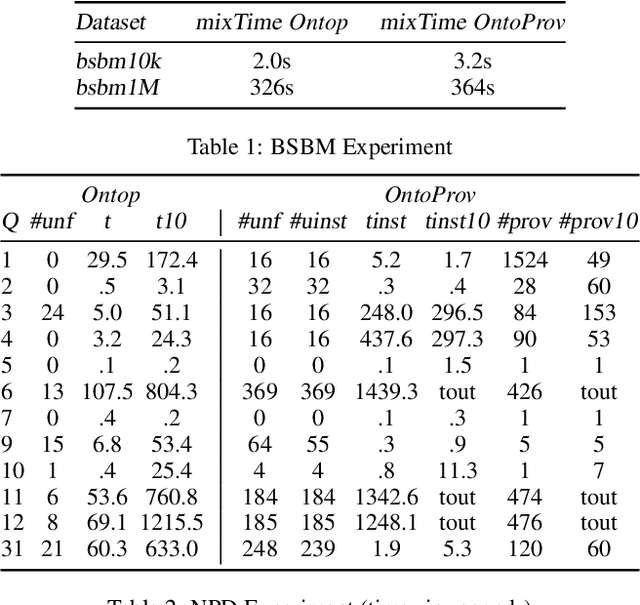
Ontology-based data access (OBDA) is a popular paradigm for querying heterogeneous data sources by connecting them through mappings to an ontology. In OBDA, it is often difficult to reconstruct why a tuple occurs in the answer of a query. We address this challenge by enriching OBDA with provenance semirings, taking inspiration from database theory. In particular, we investigate the problems of (i) deciding whether a provenance annotated OBDA instance entails a provenance annotated conjunctive query, and (ii) computing a polynomial representing the provenance of a query entailed by a provenance annotated OBDA instance. Differently from pure databases, in our case these polynomials may be infinite. To regain finiteness, we consider idempotent semirings, and study the complexity in the case of DL-Lite ontologies. We implement Task (ii) in a state-of-the-art OBDA system and show the practical feasibility of the approach through an extensive evaluation against two popular benchmarks.

Repairing Ontologies via Axiom Weakening

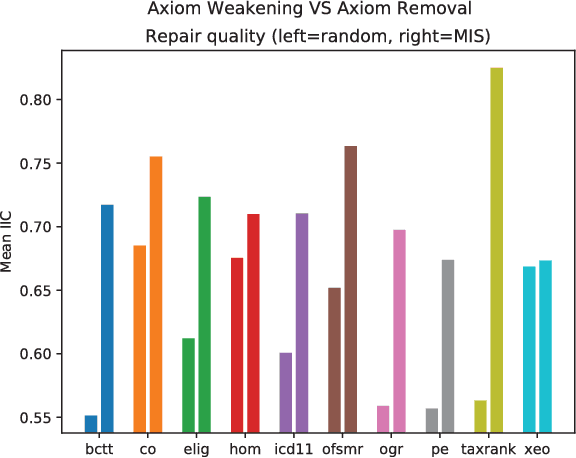
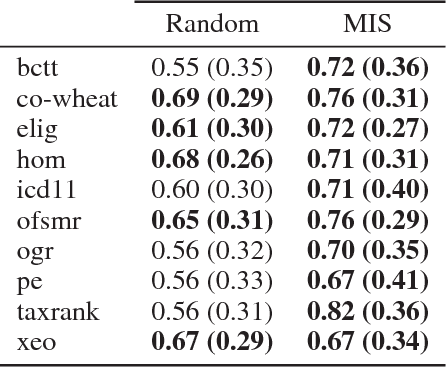
Ontology engineering is a hard and error-prone task, in which small changes may lead to errors, or even produce an inconsistent ontology. As ontologies grow in size, the need for automated methods for repairing inconsistencies while preserving as much of the original knowledge as possible increases. Most previous approaches to this task are based on removing a few axioms from the ontology to regain consistency. We propose a new method based on weakening these axioms to make them less restrictive, employing the use of refinement operators. We introduce the theoretical framework for weakening DL ontologies, propose algorithms to repair ontologies based on the framework, and provide an analysis of the computational complexity. Through an empirical analysis made over real-life ontologies, we show that our approach preserves significantly more of the original knowledge of the ontology than removing axioms.

Fuzzy Answer Set Computation via Satisfiability Modulo Theories

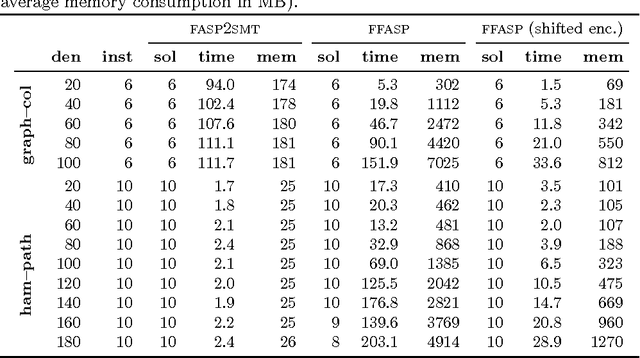
Fuzzy answer set programming (FASP) combines two declarative frameworks, answer set programming and fuzzy logic, in order to model reasoning by default over imprecise information. Several connectives are available to combine different expressions; in particular the \Godel and \Luka fuzzy connectives are usually considered, due to their properties. Although the \Godel conjunction can be easily eliminated from rule heads, we show through complexity arguments that such a simplification is infeasible in general for all other connectives. %, even if bodies are restricted to \Luka or \Godel conjunctions. The paper analyzes a translation of FASP programs into satisfiability modulo theories~(SMT), which in general produces quantified formulas because of the minimality of the semantics. Structural properties of many FASP programs allow to eliminate the quantification, or to sensibly reduce the number of quantified variables. Indeed, integrality constraints can replace recursive rules commonly used to force Boolean interpretations, and completion subformulas can guarantee minimality for acyclic programs with atomic heads. Moreover, head cycle free rules can be replaced by shifted subprograms, whose structure depends on the eliminated head connective, so that ordered completion may replace the minimality check if also \Luka disjunction in rule bodies is acyclic. The paper also presents and evaluates a prototype system implementing these translations. To appear in Theory and Practice of Logic Programming (TPLP), Proceedings of ICLP 2015.