Fuzzy Answer Set Computation via Satisfiability Modulo Theories
Paper and Code
Jul 14, 2015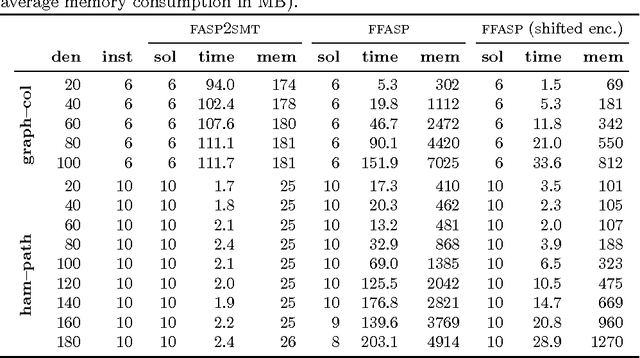
Fuzzy answer set programming (FASP) combines two declarative frameworks, answer set programming and fuzzy logic, in order to model reasoning by default over imprecise information. Several connectives are available to combine different expressions; in particular the \Godel and \Luka fuzzy connectives are usually considered, due to their properties. Although the \Godel conjunction can be easily eliminated from rule heads, we show through complexity arguments that such a simplification is infeasible in general for all other connectives. %, even if bodies are restricted to \Luka or \Godel conjunctions. The paper analyzes a translation of FASP programs into satisfiability modulo theories~(SMT), which in general produces quantified formulas because of the minimality of the semantics. Structural properties of many FASP programs allow to eliminate the quantification, or to sensibly reduce the number of quantified variables. Indeed, integrality constraints can replace recursive rules commonly used to force Boolean interpretations, and completion subformulas can guarantee minimality for acyclic programs with atomic heads. Moreover, head cycle free rules can be replaced by shifted subprograms, whose structure depends on the eliminated head connective, so that ordered completion may replace the minimality check if also \Luka disjunction in rule bodies is acyclic. The paper also presents and evaluates a prototype system implementing these translations. To appear in Theory and Practice of Logic Programming (TPLP), Proceedings of ICLP 2015.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge