On the Power and Limitations of Examples for Description Logic Concepts

Labeled examples (i.e., positive and negative examples) are an attractive medium for communicating complex concepts. They are useful for deriving concept expressions (such as in concept learning, interactive concept specification, and concept refinement) as well as for illustrating concept expressions to a user or domain expert. We investigate the power of labeled examples for describing description-logic concepts. Specifically, we systematically study the existence and efficient computability of finite characterisations, i.e. finite sets of labeled examples that uniquely characterize a single concept, for a wide variety of description logics between EL and ALCQI, both without an ontology and in the presence of a DL-Lite ontology. Finite characterisations are relevant for debugging purposes, and their existence is a necessary condition for exact learnability with membership queries.

Extracting PAC Decision Trees from Black Box Binary Classifiers: The Gender Bias Study Case on BERT-based Language Models

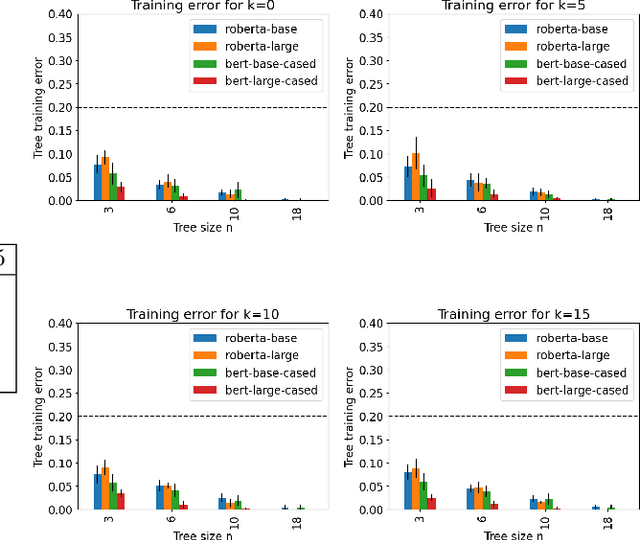
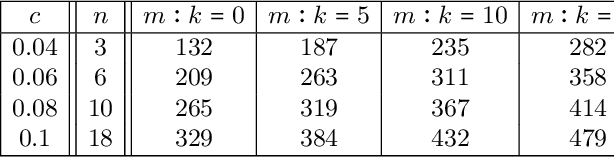
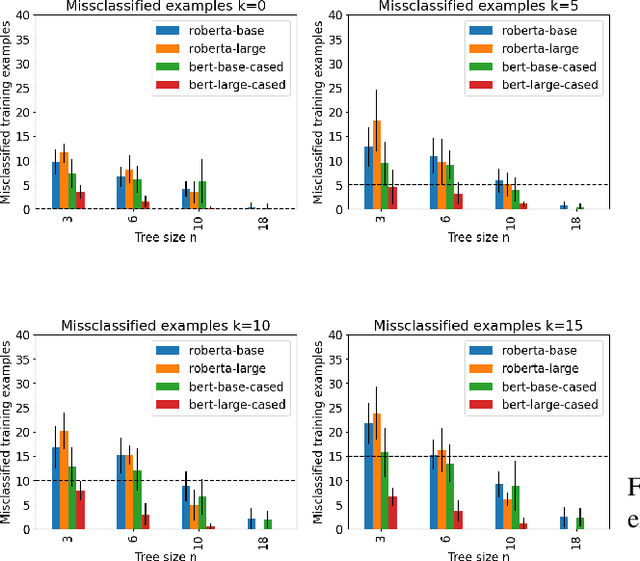
Decision trees are a popular machine learning method, known for their inherent explainability. In Explainable AI, decision trees can be used as surrogate models for complex black box AI models or as approximations of parts of such models. A key challenge of this approach is determining how accurately the extracted decision tree represents the original model and to what extent it can be trusted as an approximation of their behavior. In this work, we investigate the use of the Probably Approximately Correct (PAC) framework to provide a theoretical guarantee of fidelity for decision trees extracted from AI models. Based on theoretical results from the PAC framework, we adapt a decision tree algorithm to ensure a PAC guarantee under certain conditions. We focus on binary classification and conduct experiments where we extract decision trees from BERT-based language models with PAC guarantees. Our results indicate occupational gender bias in these models.

Knowledge Base Embeddings: Semantics and Theoretical Properties

Research on knowledge graph embeddings has recently evolved into knowledge base embeddings, where the goal is not only to map facts into vector spaces but also constrain the models so that they take into account the relevant conceptual knowledge available. This paper examines recent methods that have been proposed to embed knowledge bases in description logic into vector spaces through the lens of their geometric-based semantics. We identify several relevant theoretical properties, which we draw from the literature and sometimes generalize or unify. We then investigate how concrete embedding methods fit in this theoretical framework.

Rule Learning as Machine Translation using the Atomic Knowledge Bank

Machine learning models, and in particular language models, are being applied to various tasks that require reasoning. While such models are good at capturing patterns their ability to reason in a trustable and controlled manner is frequently questioned. On the other hand, logic-based rule systems allow for controlled inspection and already established verification methods. However it is well-known that creating such systems manually is time-consuming and prone to errors. We explore the capability of transformers to translate sentences expressing rules in natural language into logical rules. We see reasoners as the most reliable tools for performing logical reasoning and focus on translating language into the format expected by such tools. We perform experiments using the DKET dataset from the literature and create a dataset for language to logic translation based on the Atomic knowledge bank.

Semiring Provenance for Lightweight Description Logics

We investigate semiring provenance--a successful framework originally defined in the relational database setting--for description logics. In this context, the ontology axioms are annotated with elements of a commutative semiring and these annotations are propagated to the ontology consequences in a way that reflects how they are derived. We define a provenance semantics for a language that encompasses several lightweight description logics and show its relationships with semantics that have been defined for ontologies annotated with a specific kind of annotation (such as fuzzy degrees). We show that under some restrictions on the semiring, the semantics satisfies desirable properties (such as extending the semiring provenance defined for databases). We then focus on the well-known why-provenance, which allows to compute the semiring provenance for every additively and multiplicatively idempotent commutative semiring, and for which we study the complexity of problems related to the provenance of an axiom or a conjunctive query answer. Finally, we consider two more restricted cases which correspond to the so-called positive Boolean provenance and lineage in the database setting. For these cases, we exhibit relationships with well-known notions related to explanations in description logics and complete our complexity analysis. As a side contribution, we provide conditions on an ELHI_bot ontology that guarantee tractable reasoning.

Learning Horn Envelopes via Queries from Large Language Models

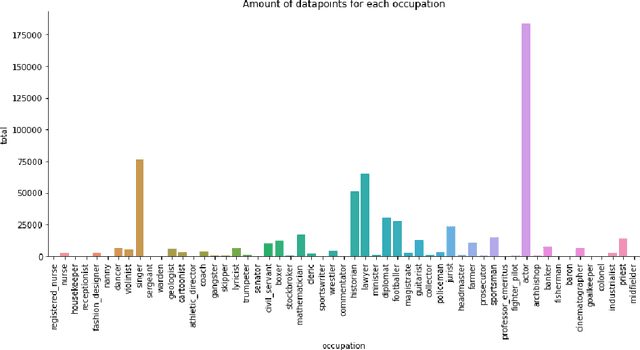
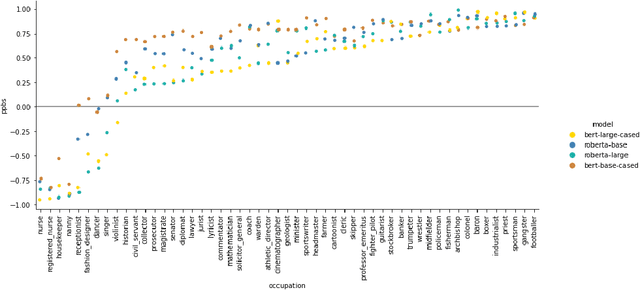
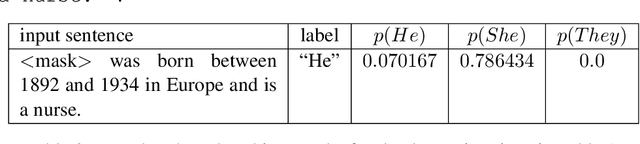
We investigate an approach for extracting knowledge from trained neural networks based on Angluin's exact learning model with membership and equivalence queries to an oracle. In this approach, the oracle is a trained neural network. We consider Angluin's classical algorithm for learning Horn theories and study the necessary changes to make it applicable to learn from neural networks. In particular, we have to consider that trained neural networks may not behave as Horn oracles, meaning that their underlying target theory may not be Horn. We propose a new algorithm that aims at extracting the ``tightest Horn approximation'' of the target theory and that is guaranteed to terminate in exponential time (in the worst case) and in polynomial time if the target has polynomially many non-Horn examples. To showcase the applicability of the approach, we perform experiments on pre-trained language models and extract rules that expose occupation-based gender biases.

Verifying Properties of Tsetlin Machines

Tsetlin Machines (TsMs) are a promising and interpretable machine learning method which can be applied for various classification tasks. We present an exact encoding of TsMs into propositional logic and formally verify properties of TsMs using a SAT solver. In particular, we introduce in this work a notion of similarity of machine learning models and apply our notion to check for similarity of TsMs. We also consider notions of robustness and equivalence from the literature and adapt them for TsMs. Then, we show the correctness of our encoding and provide results for the properties: adversarial robustness, equivalence, and similarity of TsMs. In our experiments, we employ the MNIST and IMDB datasets for (respectively) image and sentiment classification. We discuss the results for verifying robustness obtained with TsMs with those in the literature obtained with Binarized Neural Networks on MNIST.

Finding Common Ground for Incoherent Horn Expressions

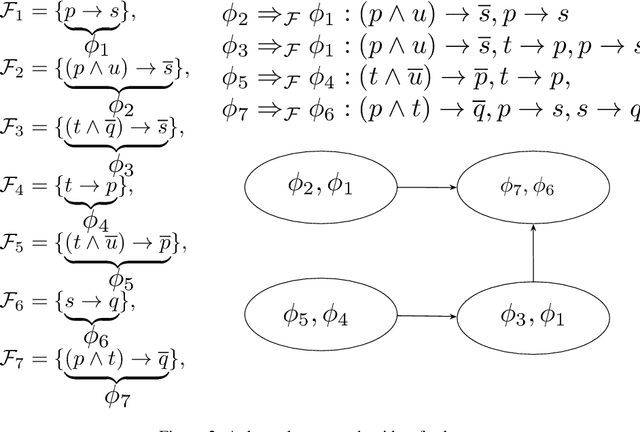
Autonomous systems that operate in a shared environment with people need to be able to follow the rules of the society they occupy. While laws are unique for one society, different people and institutions may use different rules to guide their conduct. We study the problem of reaching a common ground among possibly incoherent rules of conduct. We formally define a notion of common ground and discuss the main properties of this notion. Then, we identify three sufficient conditions on the class of Horn expressions for which common grounds are guaranteed to exist. We provide a polynomial time algorithm that computes common grounds, under these conditions. We also show that if any of the three conditions is removed then common grounds for the resulting (larger) class may not exist.

On the Effectiveness of Knowledge Graph Embeddings: a Rule Mining Approach

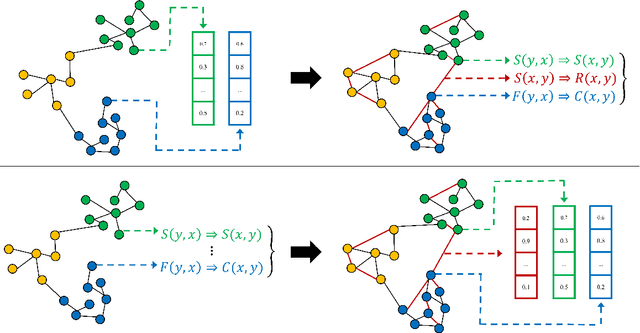
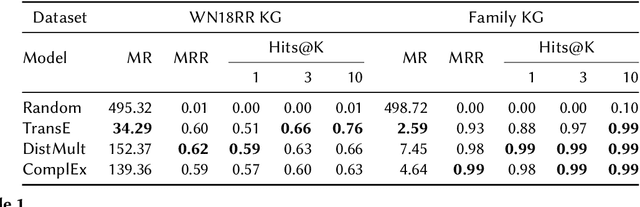
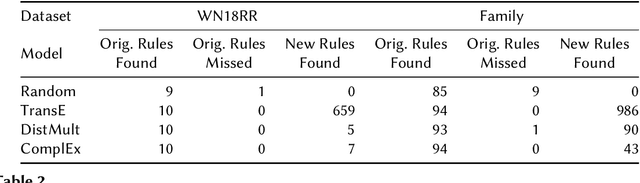
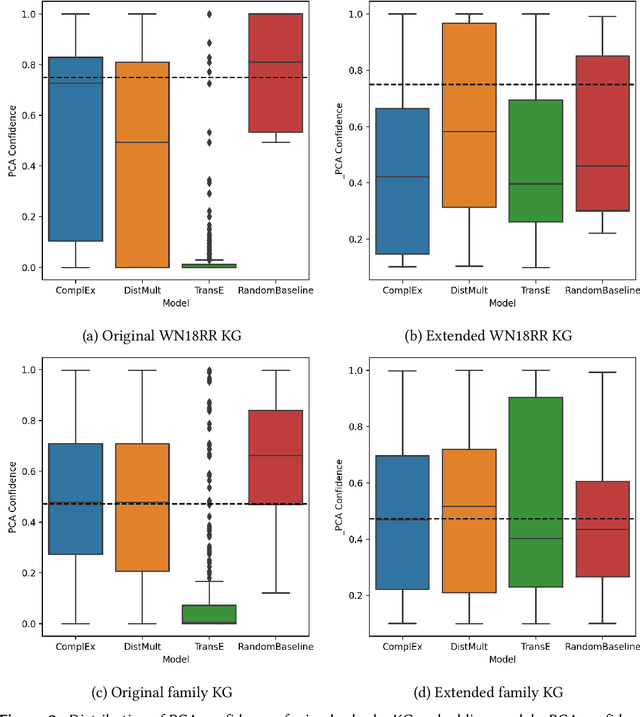
We study the effectiveness of Knowledge Graph Embeddings (KGE) for knowledge graph (KG) completion with rule mining. More specifically, we mine rules from KGs before and after they have been completed by a KGE to compare possible differences in the rules extracted. We apply this method to classical KGEs approaches, in particular, TransE, DistMult and ComplEx. Our experiments indicate that there can be huge differences between the extracted rules, depending on the KGE approach for KG completion. In particular, after the TransE completion, several spurious rules were extracted.

Extracting Rules from Neural Networks with Partial Interpretations

We investigate the problem of extracting rules, expressed in Horn logic, from neural network models. Our work is based on the exact learning model, in which a learner interacts with a teacher (the neural network model) via queries in order to learn an abstract target concept, which in our case is a set of Horn rules. We consider partial interpretations to formulate the queries. These can be understood as a representation of the world where part of the knowledge regarding the truthiness of propositions is unknown. We employ Angluin s algorithm for learning Horn rules via queries and evaluate our strategy empirically.