What Were You Thinking? An LLM-Driven Large-Scale Study of Refactoring Motivations in Open-Source Projects

Context. Code refactoring improves software quality without changing external behavior. Despite its advantages, its benefits are hindered by the considerable cost of time, resources, and continuous effort it demands. Aim. Understanding why developers refactor, and which metrics capture these motivations, may support wider and more effective use of refactoring in practice. Method. We performed a large-scale empirical study to analyze developers refactoring activity, leveraging Large Language Models (LLMs) to identify underlying motivations from version control data, comparing our findings with previous motivations reported in the literature. Results. LLMs matched human judgment in 80% of cases, but aligned with literature-based motivations in only 47%. They enriched 22% of motivations with more detailed rationale, often highlighting readability, clarity, and structural improvements. Most motivations were pragmatic, focused on simplification and maintainability. While metrics related to developer experience and code readability ranked highest, their correlation with motivation categories was weak. Conclusions. We conclude that LLMs effectively capture surface-level motivations but struggle with architectural reasoning. Their value lies in providing localized explanations, which, when combined with software metrics, can form hybrid approaches. Such integration offers a promising path toward prioritizing refactoring more systematically and balancing short-term improvements with long-term architectural goals.

Reasoning Capabilities and Invariability of Large Language Models

Large Language Models (LLMs) have shown remarkable capabilities in manipulating natural language across multiple applications, but their ability to handle simple reasoning tasks is often questioned. In this work, we aim to provide a comprehensive analysis of LLMs' reasoning competence, specifically focusing on their prompt dependency. In particular, we introduce a new benchmark dataset with a series of simple reasoning questions demanding shallow logical reasoning. Aligned with cognitive psychology standards, the questions are confined to a basic domain revolving around geometric figures, ensuring that responses are independent of any pre-existing intuition about the world and rely solely on deduction. An empirical analysis involving zero-shot and few-shot prompting across 24 LLMs of different sizes reveals that, while LLMs with over 70 billion parameters perform better in the zero-shot setting, there is still a large room for improvement. An additional test with chain-of-thought prompting over 22 LLMs shows that this additional prompt can aid or damage the performance of models, depending on whether the rationale is required before or after the answer.

Enumerating Minimal Unsatisfiable Cores of LTLf formulas

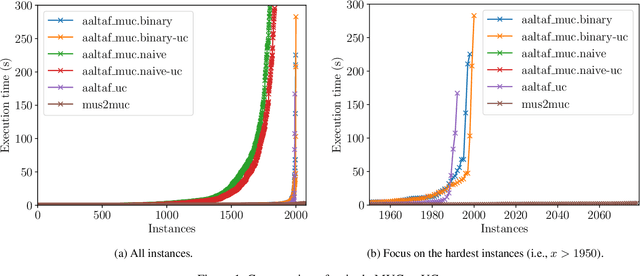
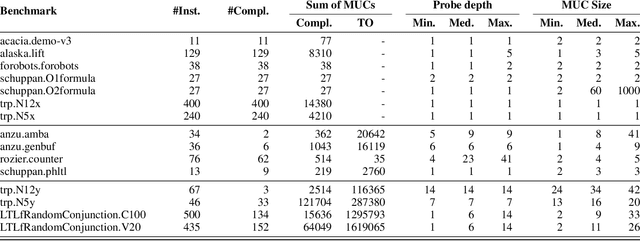
Linear Temporal Logic over finite traces ($\text{LTL}_f$) is a widely used formalism with applications in AI, process mining, model checking, and more. The primary reasoning task for $\text{LTL}_f$ is satisfiability checking; yet, the recent focus on explainable AI has increased interest in analyzing inconsistent formulas, making the enumeration of minimal explanations for infeasibility a relevant task also for $\text{LTL}_f$. This paper introduces a novel technique for enumerating minimal unsatisfiable cores (MUCs) of an $\text{LTL}_f$ specification. The main idea is to encode a $\text{LTL}_f$ formula into an Answer Set Programming (ASP) specification, such that the minimal unsatisfiable subsets (MUSes) of the ASP program directly correspond to the MUCs of the original $\text{LTL}_f$ specification. Leveraging recent advancements in ASP solving yields a MUC enumerator achieving good performance in experiments conducted on established benchmarks from the literature.

How to Blend Concepts in Diffusion Models

For the last decade, there has been a push to use multi-dimensional (latent) spaces to represent concepts; and yet how to manipulate these concepts or reason with them remains largely unclear. Some recent methods exploit multiple latent representations and their connection, making this research question even more entangled. Our goal is to understand how operations in the latent space affect the underlying concepts. To that end, we explore the task of concept blending through diffusion models. Diffusion models are based on a connection between a latent representation of textual prompts and a latent space that enables image reconstruction and generation. This task allows us to try different text-based combination strategies, and evaluate easily through a visual analysis. Our conclusion is that concept blending through space manipulation is possible, although the best strategy depends on the context of the blend.

Semiring Provenance for Lightweight Description Logics

We investigate semiring provenance--a successful framework originally defined in the relational database setting--for description logics. In this context, the ontology axioms are annotated with elements of a commutative semiring and these annotations are propagated to the ontology consequences in a way that reflects how they are derived. We define a provenance semantics for a language that encompasses several lightweight description logics and show its relationships with semantics that have been defined for ontologies annotated with a specific kind of annotation (such as fuzzy degrees). We show that under some restrictions on the semiring, the semantics satisfies desirable properties (such as extending the semiring provenance defined for databases). We then focus on the well-known why-provenance, which allows to compute the semiring provenance for every additively and multiplicatively idempotent commutative semiring, and for which we study the complexity of problems related to the provenance of an axiom or a conjunctive query answer. Finally, we consider two more restricted cases which correspond to the so-called positive Boolean provenance and lineage in the database setting. For these cases, we exhibit relationships with well-known notions related to explanations in description logics and complete our complexity analysis. As a side contribution, we provide conditions on an ELHI_bot ontology that guarantee tractable reasoning.

Answering Fuzzy Queries over Fuzzy DL-Lite Ontologies

A prominent problem in knowledge representation is how to answer queries taking into account also the implicit consequences of an ontology representing domain knowledge. While this problem has been widely studied within the realm of description logic ontologies, it has been surprisingly neglected within the context of vague or imprecise knowledge, particularly from the point of view of mathematical fuzzy logic. In this paper we study the problem of answering conjunctive queries and threshold queries w.r.t. ontologies in fuzzy DL-Lite. Specifically, we show through a rewriting approach that threshold query answering w.r.t. consistent ontologies remains in $AC_0$ in data complexity, but that conjunctive query answering is highly dependent on the selected triangular norm, which has an impact on the underlying semantics. For the idempodent G\"odel t-norm, we provide an effective method based on a reduction to the classical case. This paper is under consideration in Theory and Practice of Logic Programming (TPLP).

Union and Intersection of all Justifications

We present new algorithm for computing the union and intersection of all justifications for a given ontological consequence without first computing the set of all justifications. Through an empirical evaluation, we show that our approach works well in practice for expressive DLs. In particular, the union of all justifications can be computed much faster than with existing justification-enumeration approaches. We further discuss how to use these results to repair ontologies efficiently.

Reasoning with Contextual Knowledge and Influence Diagrams

Influence diagrams (IDs) are well-known formalisms extending Bayesian networks to model decision situations under uncertainty. Although they are convenient as a decision theoretic tool, their knowledge representation ability is limited in capturing other crucial notions such as logical consistency. We complement IDs with the light-weight description logic (DL) EL to overcome such limitations. We consider a setup where DL axioms hold in some contexts, yet the actual context is uncertain. The framework benefits from the convenience of using DL as a domain knowledge representation language and the modelling strength of IDs to deal with decisions over contexts in the presence of contextual uncertainty. We define related reasoning problems and study their computational complexity.

Axiom Pinpointing

Axiom pinpointing refers to the task of finding the specific axioms in an ontology which are responsible for a consequence to follow. This task has been studied, under different names, in many research areas, leading to a reformulation and reinvention of techniques. In this work, we present a general overview to axiom pinpointing, providing the basic notions, different approaches for solving it, and some variations and applications which have been considered in the literature. This should serve as a starting point for researchers interested in related problems, with an ample bibliography for delving deeper into the details.

Provenance for the Description Logic ELHr

We address the problem of handling provenance information in ELHr ontologies. We consider a setting recently introduced for ontology-based data access, based on semirings and extending classical data provenance, in which ontology axioms are annotated with provenance tokens. A consequence inherits the provenance of the axioms involved in deriving it, yielding a provenance polynomial as an annotation. We analyse the semantics for the ELHr case and show that the presence of conjunctions poses various difficulties for handling provenance, some of which are mitigated by assuming multiplicative idempotency of the semiring. Under this assumption, we study three problems: ontology completion with provenance, computing the set of relevant axioms for a consequence, and query answering.