Generating Counterfactual Explanations Under Temporal Constraints

Counterfactual explanations are one of the prominent eXplainable Artificial Intelligence (XAI) techniques, and suggest changes to input data that could alter predictions, leading to more favourable outcomes. Existing counterfactual methods do not readily apply to temporal domains, such as that of process mining, where data take the form of traces of activities that must obey to temporal background knowledge expressing which dynamics are possible and which not. Specifically, counterfactuals generated off-the-shelf may violate the background knowledge, leading to inconsistent explanations. This work tackles this challenge by introducing a novel approach for generating temporally constrained counterfactuals, guaranteed to comply by design with background knowledge expressed in Linear Temporal Logic on process traces (LTLp). We do so by infusing automata-theoretic techniques for LTLp inside a genetic algorithm for counterfactual generation. The empirical evaluation shows that the generated counterfactuals are temporally meaningful and more interpretable for applications involving temporal dependencies.

Conformance Checking of Fuzzy Logs against Declarative Temporal Specifications

Traditional conformance checking tasks assume that event data provide a faithful and complete representation of the actual process executions. This assumption has been recently questioned: more and more often events are not traced explicitly, but are instead indirectly obtained as the result of event recognition pipelines, and thus inherently come with uncertainty. In this work, differently from the typical probabilistic interpretation of uncertainty, we consider the relevant case where uncertainty refers to which activity is actually conducted, under a fuzzy semantics. In this novel setting, we consider the problem of checking whether fuzzy event data conform with declarative temporal rules specified as Declare patterns or, more generally, as formulae of linear temporal logic over finite traces (LTLf). This requires to relax the assumption that at each instant only one activity is executed, and to correspondingly redefine boolean operators of the logic with a fuzzy semantics. Specifically, we provide a threefold contribution. First, we define a fuzzy counterpart of LTLf tailored to our purpose. Second, we cast conformance checking over fuzzy logs as a verification problem in this logic. Third, we provide a proof-of-concept, efficient implementation based on the PyTorch Python library, suited to check conformance of multiple fuzzy traces at once.

Depth-Bounded Epistemic Planning

In this paper, we propose a novel algorithm for epistemic planning based on dynamic epistemic logic (DEL). The novelty is that we limit the depth of reasoning of the planning agent to an upper bound b, meaning that the planning agent can only reason about higher-order knowledge to at most (modal) depth b. The algorithm makes use of a novel type of canonical b-bisimulation contraction guaranteeing unique minimal models with respect to b-bisimulation. We show our depth-bounded planning algorithm to be sound. Additionally, we show it to be complete with respect to planning tasks having a solution within bound b of reasoning depth (and hence the iterative bound-deepening variant is complete in the standard sense). For bound b of reasoning depth, the algorithm is shown to be (b + 1)-EXPTIME complete, and furthermore fixed-parameter tractable in the number of agents and atoms. We present both a tree search and a graph search variant of the algorithm, and we benchmark an implementation of the tree search version against a baseline epistemic planner.

Object-Centric Conformance Alignments with Synchronization (Extended Version)

Real-world processes operate on objects that are inter-dependent. To accurately reflect the nature of such processes, object-centric process mining techniques are needed, notably conformance checking. However, while the object-centric perspective has recently gained traction, few concrete process mining techniques have been presented so far. Moreover, existing approaches are severely limited in their abilities to keep track of object identity and object dependencies. Consequently, serious problems in logs remain undetected. In this paper, we present a new formalism that combines the key modelling features of two existing approaches, in particular the ability of object-centric Petri nets to capture one-to-many relations and the one of Petri nets with identifiers to compare and synchronize objects based on their identity. We call the resulting formalism 'object-centric Petri nets with identifiers', and define alignments and the conformance checking task for this setting. We propose a conformance checking approach for such nets based on an encoding in satisfiability modulo theories (SMT), and illustrate how it can be effectively used to overcome shortcomings of earlier work. To assess its practicality, we perform an evaluation on data from the literature.

DELPHIC: Practical DEL Planning via Possibilities (Extended Version)

Dynamic Epistemic Logic (DEL) provides a framework for epistemic planning that is capable of representing non-deterministic actions, partial observability, higher-order knowledge and both factual and epistemic change. The high expressivity of DEL challenges existing epistemic planners, which typically can handle only restricted fragments of the whole framework. The goal of this work is to push the envelop of practical DEL planning, ultimately aiming for epistemic planners to be able to deal with the full range of features offered by DEL. Towards this goal, we question the traditional semantics of DEL, defined in terms on Kripke models. In particular, we propose an equivalent semantics defined using, as main building block, so-called possibilities: non well-founded objects representing both factual properties of the world, and what agents consider to be possible. We call the resulting framework DELPHIC. We argue that DELPHIC indeed provides a more compact representation of epistemic states. To substantiate this claim, we implement both approaches in ASP and we set up an experimental evaluation to compare DELPHIC with the traditional, Kripke-based approach. The evaluation confirms that DELPHIC outperforms the traditional approach in space and time.

A Semantic Approach to Decidability in Epistemic Planning (Extended Version)

The use of Dynamic Epistemic Logic (DEL) in multi-agent planning has led to a widely adopted action formalism that can handle nondeterminism, partial observability and arbitrary knowledge nesting. As such expressive power comes at the cost of undecidability, several decidable fragments have been isolated, mainly based on syntactic restrictions of the action formalism. In this paper, we pursue a novel semantic approach to achieve decidability. Namely, rather than imposing syntactical constraints, the semantic approach focuses on the axioms of the logic for epistemic planning. Specifically, we augment the logic of knowledge S5$_n$ and with an interaction axiom called (knowledge) commutativity, which controls the ability of agents to unboundedly reason on the knowledge of other agents. We then provide a threefold contribution. First, we show that the resulting epistemic planning problem is decidable. In doing so, we prove that our framework admits a finitary non-fixpoint characterization of common knowledge, which is of independent interest. Second, we study different generalizations of the commutativity axiom, with the goal of obtaining decidability for more expressive fragments of DEL. Finally, we show that two well-known epistemic planning systems based on action templates, when interpreted under the setting of knowledge, conform to the commutativity axiom, hence proving their decidability.

Enjoy the Silence: Analysis of Stochastic Petri Nets with Silent Transitions

Capturing stochastic behaviors in business and work processes is essential to quantitatively understand how nondeterminism is resolved when taking decisions within the process. This is of special interest in process mining, where event data tracking the actual execution of the process are related to process models, and can then provide insights on frequencies and probabilities. Variants of stochastic Petri nets provide a natural formal basis for this. However, when capturing processes, such nets need to be labelled with (possibly duplicated) activities, and equipped with silent transitions that model internal, non-logged steps related to the orchestration of the process. At the same time, they have to be analyzed in a finite-trace semantics, matching the fact that each process execution consists of finitely many steps. These two aspects impede the direct application of existing techniques for stochastic Petri nets, calling for a novel characterization that incorporates labels and silent transitions in a finite-trace semantics. In this article, we provide such a characterization starting from generalized stochastic Petri nets and obtaining the framework of labelled stochastic processes (LSPs). On top of this framework, we introduce different key analysis tasks on the traces of LSPs and their probabilities. We show that all such analysis tasks can be solved analytically, in particular reducing them to a single method that combines automata-based techniques to single out the behaviors of interest within a LSP, with techniques based on absorbing Markov chains to reason on their probabilities. Finally, we demonstrate the significance of how our approach in the context of stochastic conformance checking, illustrating practical feasibility through a proof-of-concept implementation and its application to different datasets.

Relational Action Bases: Formalization, Effective Safety Verification, and Invariants (Extended Version)

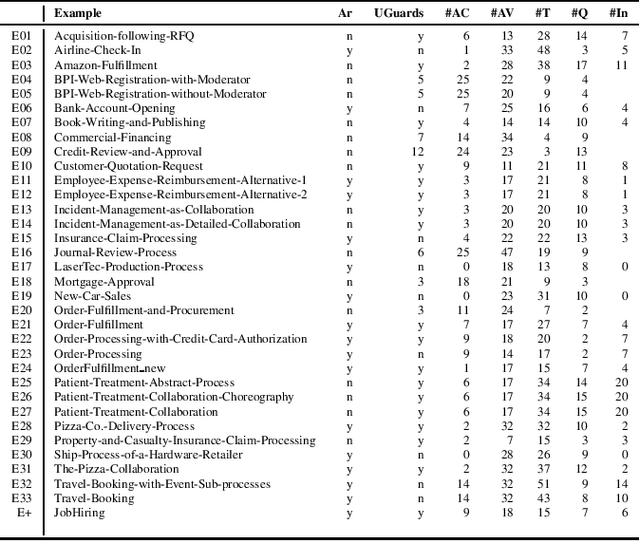
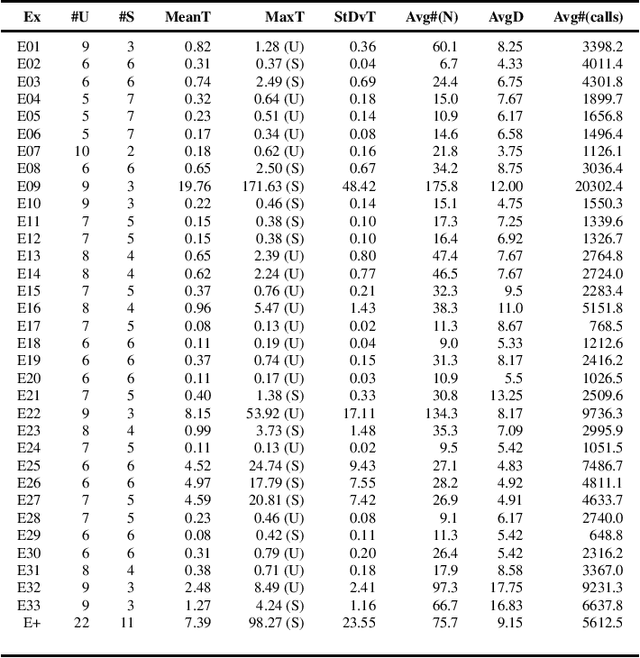
Modeling and verification of dynamic systems operating over a relational representation of states are increasingly investigated problems in AI, Business Process Management, and Database Theory. To make these systems amenable to verification, the amount of information stored in each relational state needs to be bounded, or restrictions are imposed on the preconditions and effects of actions. We introduce the general framework of relational action bases (RABs), which generalizes existing models by lifting both these restrictions: unbounded relational states can be evolved through actions that can quantify both existentially and universally over the data, and that can exploit numerical datatypes with arithmetic predicates. We then study parameterized safety of RABs via (approximated) SMT-based backward search, singling out essential meta-properties of the resulting procedure, and showing how it can be realized by an off-the-shelf combination of existing verification modules of the state-of-the-art MCMT model checker. We demonstrate the effectiveness of this approach on a benchmark of data-aware business processes. Finally, we show how universal invariants can be exploited to make this procedure fully correct.

Conformance Checking with Uncertainty via SMT (Extended Version)

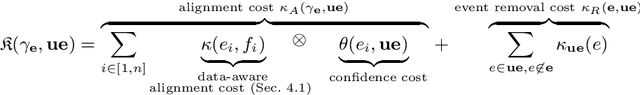
Logs of real-life processes often feature uncertainty pertaining the recorded timestamps, data values, and/or events. We consider the problem of checking conformance of uncertain logs against data-aware reference processes. Specifically, we show how to solve it via SMT encodings, lifting previous work on data-aware SMT-based conformance checking to this more sophisticated setting. Our approach is modular, in that it homogeneously accommodates for different types of uncertainty. Moreover, using appropriate cost functions, different conformance checking tasks can be addressed. We show the correctness of our approach and witness feasibility through a proof-of-concept implementation.

Soundness of Data-Aware Processes with Arithmetic Conditions

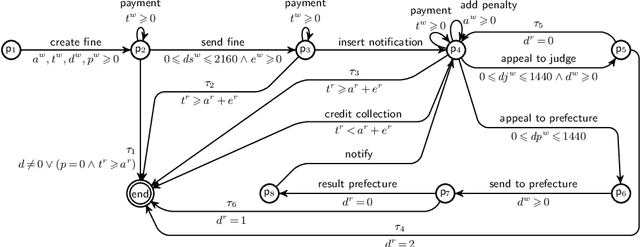
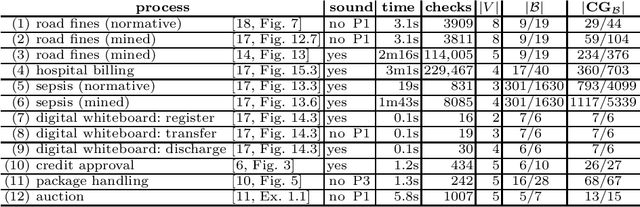
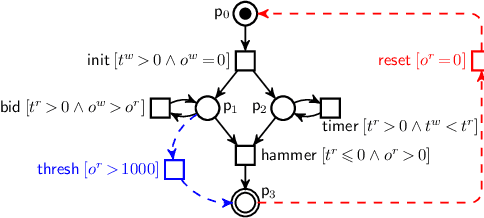
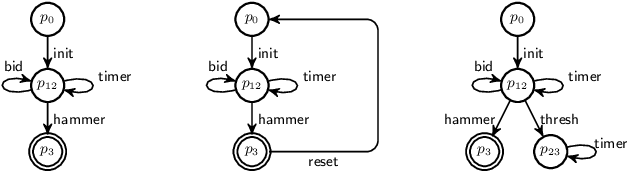
Data-aware processes represent and integrate structural and behavioural constraints in a single model, and are thus increasingly investigated in business process management and information systems engineering. In this spectrum, Data Petri nets (DPNs) have gained increasing popularity thanks to their ability to balance simplicity with expressiveness. The interplay of data and control-flow makes checking the correctness of such models, specifically the well-known property of soundness, crucial and challenging. A major shortcoming of previous approaches for checking soundness of DPNs is that they consider data conditions without arithmetic, an essential feature when dealing with real-world, concrete applications. In this paper, we attack this open problem by providing a foundational and operational framework for assessing soundness of DPNs enriched with arithmetic data conditions. The framework comes with a proof-of-concept implementation that, instead of relying on ad-hoc techniques, employs off-the-shelf established SMT technologies. The implementation is validated on a collection of examples from the literature, and on synthetic variants constructed from such examples.