Stochastic Alignments: Matching an Observed Trace to Stochastic Process Models

Process mining leverages event data extracted from IT systems to generate insights into the business processes of organizations. Such insights benefit from explicitly considering the frequency of behavior in business processes, which is captured by stochastic process models. Given an observed trace and a stochastic process model, conventional alignment-based conformance checking techniques face a fundamental limitation: They prioritize matching the trace to a model path with minimal deviations, which may, however, lead to selecting an unlikely path. In this paper, we study the problem of matching an observed trace to a stochastic process model by identifying a likely model path with a low edit distance to the trace. We phrase this as an optimization problem and develop a heuristic-guided path-finding algorithm to solve it. Our open-source implementation demonstrates the feasibility of the approach and shows that it can provide new, useful diagnostic insights for analysts.

Technical Report with Proofs for A Full Picture in Conformance Checking: Efficiently Summarizing All Optimal Alignments

This technical report provides proofs for the claims in the paper "A Full Picture in Conformance Checking: Efficiently Summarizing All Optimal Alignments".

Enjoy the Silence: Analysis of Stochastic Petri Nets with Silent Transitions

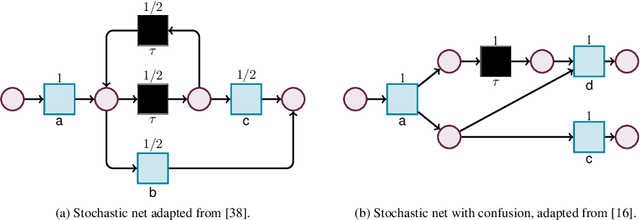
Capturing stochastic behaviors in business and work processes is essential to quantitatively understand how nondeterminism is resolved when taking decisions within the process. This is of special interest in process mining, where event data tracking the actual execution of the process are related to process models, and can then provide insights on frequencies and probabilities. Variants of stochastic Petri nets provide a natural formal basis for this. However, when capturing processes, such nets need to be labelled with (possibly duplicated) activities, and equipped with silent transitions that model internal, non-logged steps related to the orchestration of the process. At the same time, they have to be analyzed in a finite-trace semantics, matching the fact that each process execution consists of finitely many steps. These two aspects impede the direct application of existing techniques for stochastic Petri nets, calling for a novel characterization that incorporates labels and silent transitions in a finite-trace semantics. In this article, we provide such a characterization starting from generalized stochastic Petri nets and obtaining the framework of labelled stochastic processes (LSPs). On top of this framework, we introduce different key analysis tasks on the traces of LSPs and their probabilities. We show that all such analysis tasks can be solved analytically, in particular reducing them to a single method that combines automata-based techniques to single out the behaviors of interest within a LSP, with techniques based on absorbing Markov chains to reason on their probabilities. Finally, we demonstrate the significance of how our approach in the context of stochastic conformance checking, illustrating practical feasibility through a proof-of-concept implementation and its application to different datasets.

Language-Preserving Reduction Rules for Block-Structured Workflow Nets

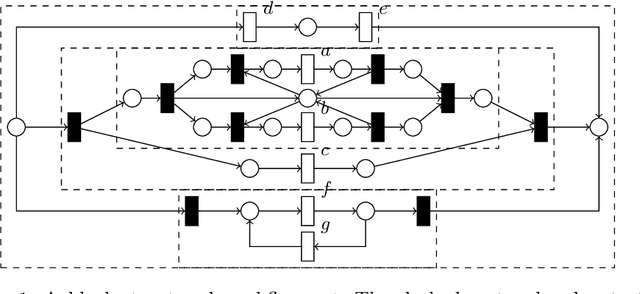
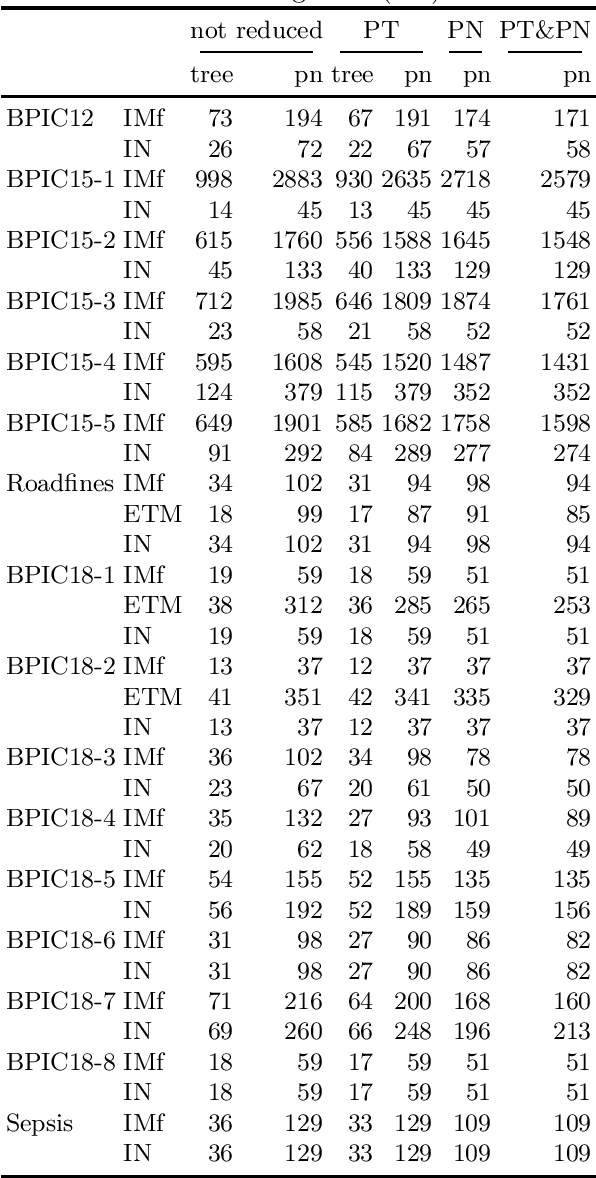
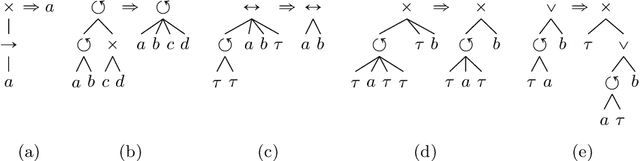
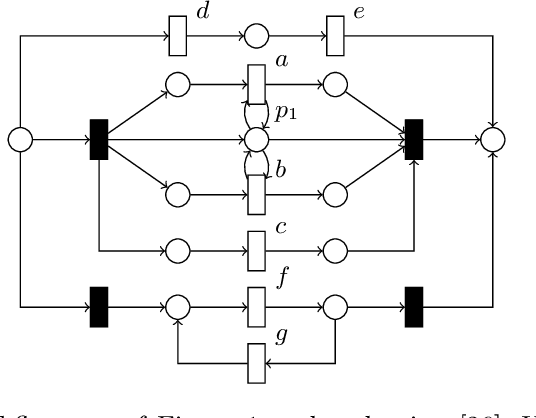
Process models are used by human analysts to model and analyse behaviour, and by machines to verify properties such as soundness, liveness or other reachability properties, and to compare their expressed behaviour with recorded behaviour within business processes of organisations. For both human and machine use, small models are preferable over large and complex models: for ease of human understanding and to reduce the time spent by machines in state space explorations. Reduction rules that preserve the behaviour of models have been defined for Petri nets, however in this paper we show that a subclass of Petri nets returned by process discovery techniques, that is, block-structured workflow nets, can be further reduced by considering their block structure in process trees. We revisit an existing set of reduction rules for process trees and show that the rules are correct, terminating, confluent and complete, and for which classes of process trees they are and are not complete. In a real-life experiment, we show that these rules can reduce process models discovered from real-life event logs further compared with rules that consider only Petri net structures.

Entropia: A Family of Entropy-Based Conformance Checking Measures for Process Mining

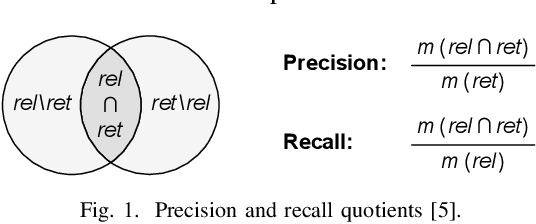
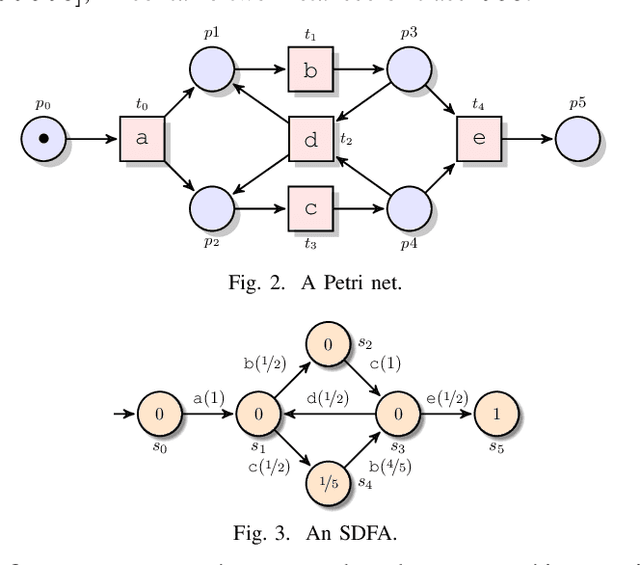
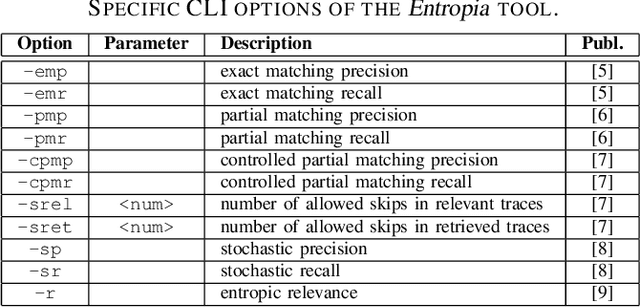
This paper presents a command-line tool, called Entropia, that implements a family of conformance checking measures for process mining founded on the notion of entropy from information theory. The measures allow quantifying classical non-deterministic and stochastic precision and recall quality criteria for process models automatically discovered from traces executed by IT-systems and recorded in their event logs. A process model has "good" precision with respect to the log it was discovered from if it does not encode many traces that are not part of the log, and has "good" recall if it encodes most of the traces from the log. By definition, the measures possess useful properties and can often be computed quickly.