Enjoy the Silence: Analysis of Stochastic Petri Nets with Silent Transitions

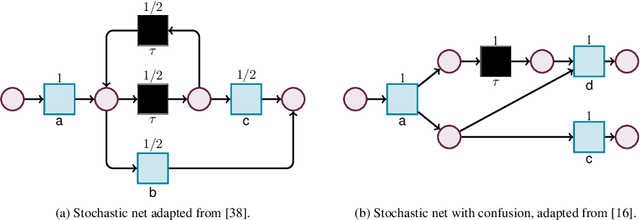
Capturing stochastic behaviors in business and work processes is essential to quantitatively understand how nondeterminism is resolved when taking decisions within the process. This is of special interest in process mining, where event data tracking the actual execution of the process are related to process models, and can then provide insights on frequencies and probabilities. Variants of stochastic Petri nets provide a natural formal basis for this. However, when capturing processes, such nets need to be labelled with (possibly duplicated) activities, and equipped with silent transitions that model internal, non-logged steps related to the orchestration of the process. At the same time, they have to be analyzed in a finite-trace semantics, matching the fact that each process execution consists of finitely many steps. These two aspects impede the direct application of existing techniques for stochastic Petri nets, calling for a novel characterization that incorporates labels and silent transitions in a finite-trace semantics. In this article, we provide such a characterization starting from generalized stochastic Petri nets and obtaining the framework of labelled stochastic processes (LSPs). On top of this framework, we introduce different key analysis tasks on the traces of LSPs and their probabilities. We show that all such analysis tasks can be solved analytically, in particular reducing them to a single method that combines automata-based techniques to single out the behaviors of interest within a LSP, with techniques based on absorbing Markov chains to reason on their probabilities. Finally, we demonstrate the significance of how our approach in the context of stochastic conformance checking, illustrating practical feasibility through a proof-of-concept implementation and its application to different datasets.

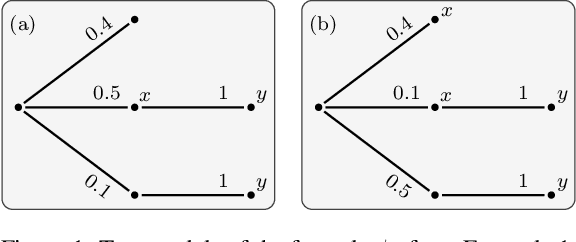
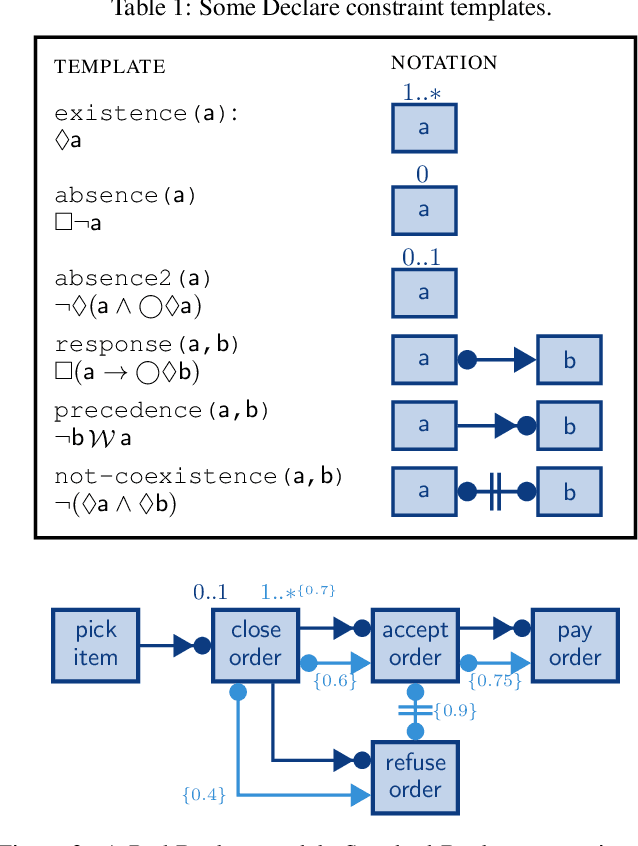
Probabilistic Temporal Logic over Finite Traces (Technical Report)

Temporal logics over finite traces have recently gained attention due to their use in real-world applications, in particular in business process modelling and planning. In real life, processes contain some degree of uncertainty that is impossible to handle with classical logics. We propose a new probabilistic temporal logic over finite traces based on superposition semantics, where all possible evolutions are possible, until observed. We study the properties of the logic and provide automata-based mechanisms for deriving probabilistic inferences from its formulas. We ground the approach in the context of declarative process modelling, showing how the temporal patterns used in Declare can be lifted to our setting, and discussing how probabilistic inferences can be exploited to provide key offline and runtime reasoning tasks, and how to discover probabilistic Declare patterns from event data by minor adjustments to existing discovery algorithms.

Discovering Process Maps from Event Streams

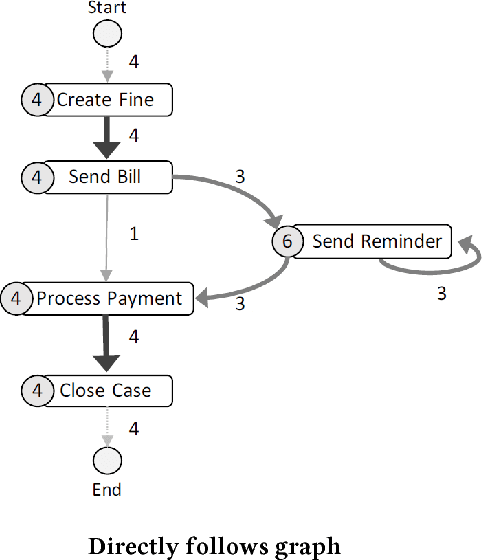
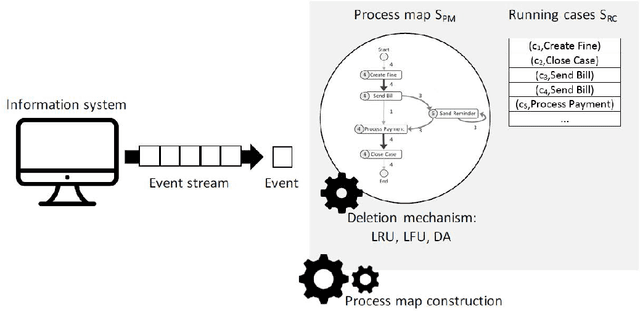
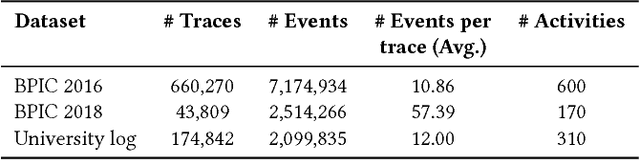
Automated process discovery is a class of process mining methods that allow analysts to extract business process models from event logs. Traditional process discovery methods extract process models from a snapshot of an event log stored in its entirety. In some scenarios, however, events keep coming with a high arrival rate to the extent that it is impractical to store the entire event log and to continuously re-discover a process model from scratch. Such scenarios require online process discovery approaches. Given an event stream produced by the execution of a business process, the goal of an online process discovery method is to maintain a continuously updated model of the process with a bounded amount of memory while at the same time achieving similar accuracy as offline methods. However, existing online discovery approaches require relatively large amounts of memory to achieve levels of accuracy comparable to that of offline methods. Therefore, this paper proposes an approach that addresses this limitation by mapping the problem of online process discovery to that of cache memory management, and applying well-known cache replacement policies to the problem of online process discovery. The approach has been implemented in .NET, experimentally integrated with the Minit process mining tool and comparatively evaluated against an existing baseline using real-life datasets.