Relational Action Bases: Formalization, Effective Safety Verification, and Invariants (Extended Version)
Paper and Code
Aug 12, 2022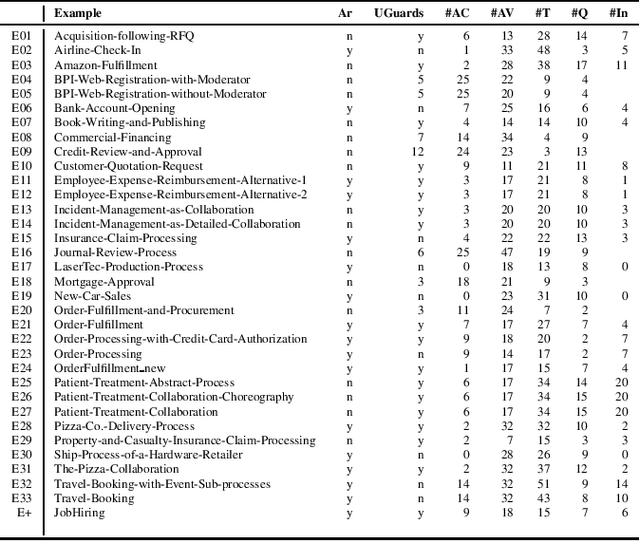
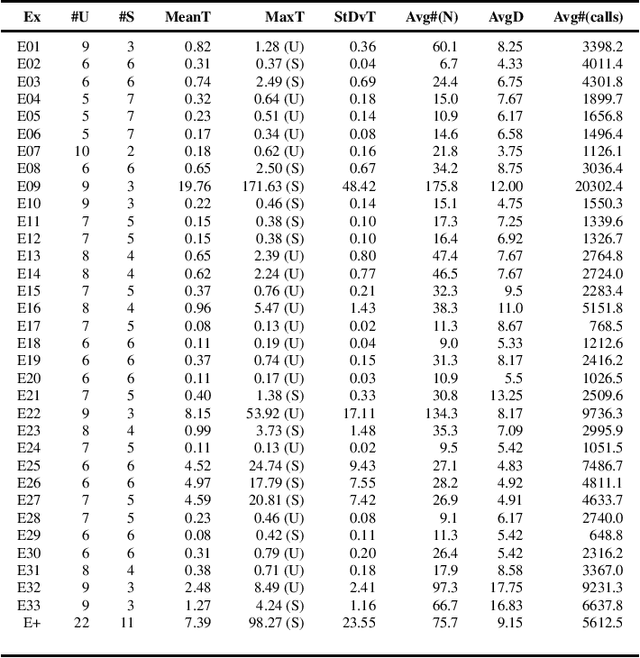
Modeling and verification of dynamic systems operating over a relational representation of states are increasingly investigated problems in AI, Business Process Management, and Database Theory. To make these systems amenable to verification, the amount of information stored in each relational state needs to be bounded, or restrictions are imposed on the preconditions and effects of actions. We introduce the general framework of relational action bases (RABs), which generalizes existing models by lifting both these restrictions: unbounded relational states can be evolved through actions that can quantify both existentially and universally over the data, and that can exploit numerical datatypes with arithmetic predicates. We then study parameterized safety of RABs via (approximated) SMT-based backward search, singling out essential meta-properties of the resulting procedure, and showing how it can be realized by an off-the-shelf combination of existing verification modules of the state-of-the-art MCMT model checker. We demonstrate the effectiveness of this approach on a benchmark of data-aware business processes. Finally, we show how universal invariants can be exploited to make this procedure fully correct.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge