Enumerating Minimal Unsatisfiable Cores of LTLf formulas

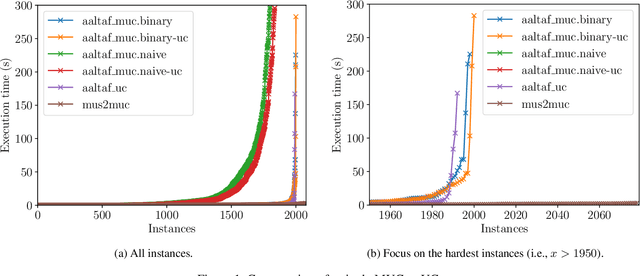
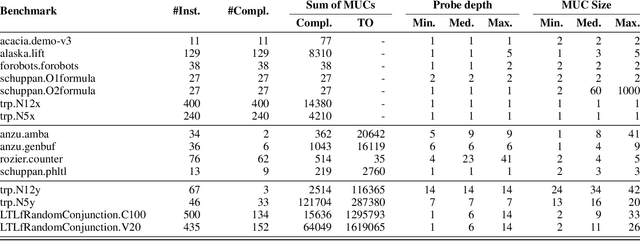
Linear Temporal Logic over finite traces ($\text{LTL}_f$) is a widely used formalism with applications in AI, process mining, model checking, and more. The primary reasoning task for $\text{LTL}_f$ is satisfiability checking; yet, the recent focus on explainable AI has increased interest in analyzing inconsistent formulas, making the enumeration of minimal explanations for infeasibility a relevant task also for $\text{LTL}_f$. This paper introduces a novel technique for enumerating minimal unsatisfiable cores (MUCs) of an $\text{LTL}_f$ specification. The main idea is to encode a $\text{LTL}_f$ formula into an Answer Set Programming (ASP) specification, such that the minimal unsatisfiable subsets (MUSes) of the ASP program directly correspond to the MUCs of the original $\text{LTL}_f$ specification. Leveraging recent advancements in ASP solving yields a MUC enumerator achieving good performance in experiments conducted on established benchmarks from the literature.

Quantifying over Optimum Answer Sets

Answer Set Programming with Quantifiers (ASP(Q)) has been introduced to provide a natural extension of ASP modeling to problems in the polynomial hierarchy (PH). However, ASP(Q) lacks a method for encoding in an elegant and compact way problems requiring a polynomial number of calls to an oracle in $\Sigma_n^p$ (that is, problems in $\Delta_{n+1}^p$). Such problems include, in particular, optimization problems. In this paper we propose an extension of ASP(Q), in which component programs may contain weak constraints. Weak constraints can be used both for expressing local optimization within quantified component programs and for modeling global optimization criteria. We showcase the modeling capabilities of the new formalism through various application scenarios. Further, we study its computational properties obtaining complexity results and unveiling non-obvious characteristics of ASP(Q) programs with weak constraints.

Unit Testing in ASP Revisited: Language and Test-Driven Development Environment

Unit testing frameworks are nowadays considered a best practice, included in almost all modern software development processes, to achieve rapid development of correct specifications. Knowledge representation and reasoning paradigms such as Answer Set Programming (ASP), that have been used in industry-level applications, are not an exception. Indeed, the first unit testing specification language for ASP was proposed in 2011 as a feature of the ASPIDE development environment. Later, a more portable unit testing language was included in the LANA annotation language. In this paper we revisit both languages and tools for unit testing in ASP. We propose a new unit test specification language that allows one to inline tests within ASP programs, and we identify the computational complexity of the tasks associated with checking the various program-correctness assertions. Test-case specifications are transparent to the traditional evaluation, but can be interpreted by a specific testing tool. Thus, we present a novel environment supporting test driven development of ASP programs.

An efficient solver for ASP(Q)

Answer Set Programming with Quantifiers ASP(Q) extends Answer Set Programming (ASP) to allow for declarative and modular modeling of problems from the entire polynomial hierarchy. The first implementation of ASP(Q), called qasp, was based on a translation to Quantified Boolean Formulae (QBF) with the aim of exploiting the well-developed and mature QBF-solving technology. However, the implementation of the QBF encoding employed in qasp is very general and might produce formulas that are hard to evaluate for existing QBF solvers because of the large number of symbols and sub-clauses. In this paper, we present a new implementation that builds on the ideas of qasp and features both a more efficient encoding procedure and new optimized encodings of ASP(Q) programs in QBF. The new encodings produce smaller formulas (in terms of the number of quantifiers, variables, and clauses) and result in a more efficient evaluation process. An algorithm selection strategy automatically combines several QBF-solving back-ends to further increase performance. An experimental analysis, conducted on known benchmarks, shows that the new system outperforms qasp.