Giovanni Amendola
Navigating Taxonomic Expansions of Entity Sets Driven by Knowledge Bases
Dec 17, 2025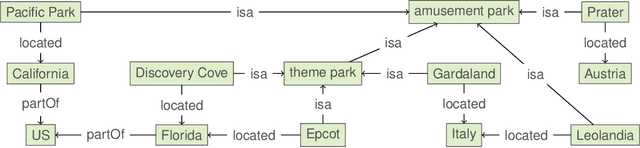

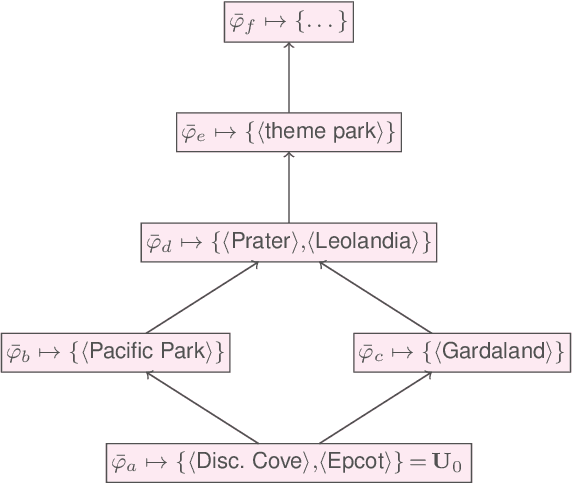

Abstract:Recognizing similarities among entities is central to both human cognition and computational intelligence. Within this broader landscape, Entity Set Expansion is one prominent task aimed at taking an initial set of (tuples of) entities and identifying additional ones that share relevant semantic properties with the former -- potentially repeating the process to form increasingly broader sets. However, this ``linear'' approach does not unveil the richer ``taxonomic'' structures present in knowledge resources. A recent logic-based framework introduces the notion of an expansion graph: a rooted directed acyclic graph where each node represents a semantic generalization labeled by a logical formula, and edges encode strict semantic inclusion. This structure supports taxonomic expansions of entity sets driven by knowledge bases. Yet, the potentially large size of such graphs may make full materialization impractical in real-world scenarios. To overcome this, we formalize reasoning tasks that check whether two tuples belong to comparable, incomparable, or the same nodes in the graph. Our results show that, under realistic assumptions -- such as bounding the input or limiting entity descriptions -- these tasks can be implemented efficiently. This enables local, incremental navigation of expansion graphs, supporting practical applications without requiring full graph construction.
Unit Testing in ASP Revisited: Language and Test-Driven Development Environment
Jan 04, 2024Abstract:Unit testing frameworks are nowadays considered a best practice, included in almost all modern software development processes, to achieve rapid development of correct specifications. Knowledge representation and reasoning paradigms such as Answer Set Programming (ASP), that have been used in industry-level applications, are not an exception. Indeed, the first unit testing specification language for ASP was proposed in 2011 as a feature of the ASPIDE development environment. Later, a more portable unit testing language was included in the LANA annotation language. In this paper we revisit both languages and tools for unit testing in ASP. We propose a new unit test specification language that allows one to inline tests within ASP programs, and we identify the computational complexity of the tasks associated with checking the various program-correctness assertions. Test-case specifications are transparent to the traditional evaluation, but can be interpreted by a specific testing tool. Thus, we present a novel environment supporting test driven development of ASP programs.
Characterizing Nexus of Similarity within Knowledge Bases: A Logic-based Framework and its Computational Complexity Aspects
Mar 19, 2023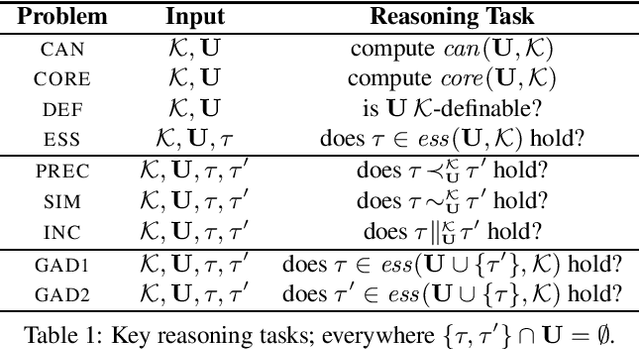
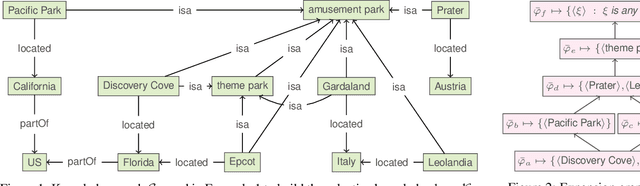
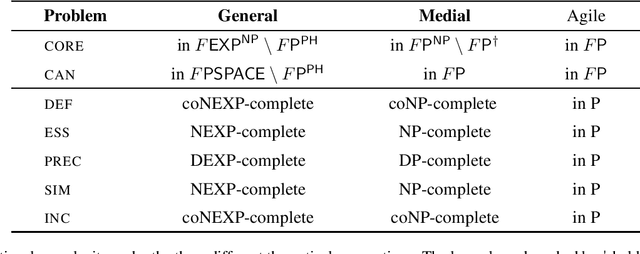

Abstract:Similarities between entities occur frequently in many real-world scenarios. For over a century, researchers in different fields have proposed a range of approaches to measure the similarity between entities. More recently, inspired by "Google Sets", significant academic and commercial efforts have been devoted to expanding a given set of entities with similar ones. As a result, existing approaches nowadays are able to take into account properties shared by entities, hereinafter called nexus of similarity. Accordingly, machines are largely able to deal with both similarity measures and set expansions. To the best of our knowledge, however, there is no way to characterize nexus of similarity between entities, namely identifying such nexus in a formal and comprehensive way so that they are both machine- and human-readable; moreover, there is a lack of consensus on evaluating existing approaches for weakly similar entities. As a first step towards filling these gaps, we aim to complement existing literature by developing a novel logic-based framework to formally and automatically characterize nexus of similarity between tuples of entities within a knowledge base. Furthermore, we analyze computational complexity aspects of this framework.
Better Paracoherent Answer Sets with Less Resources
Jul 22, 2019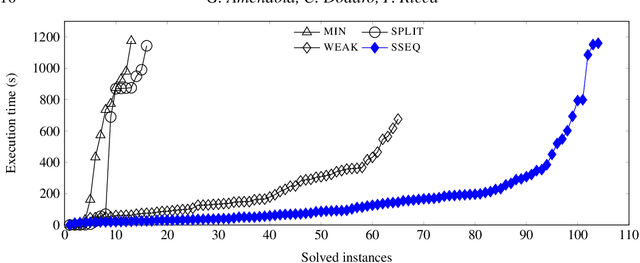
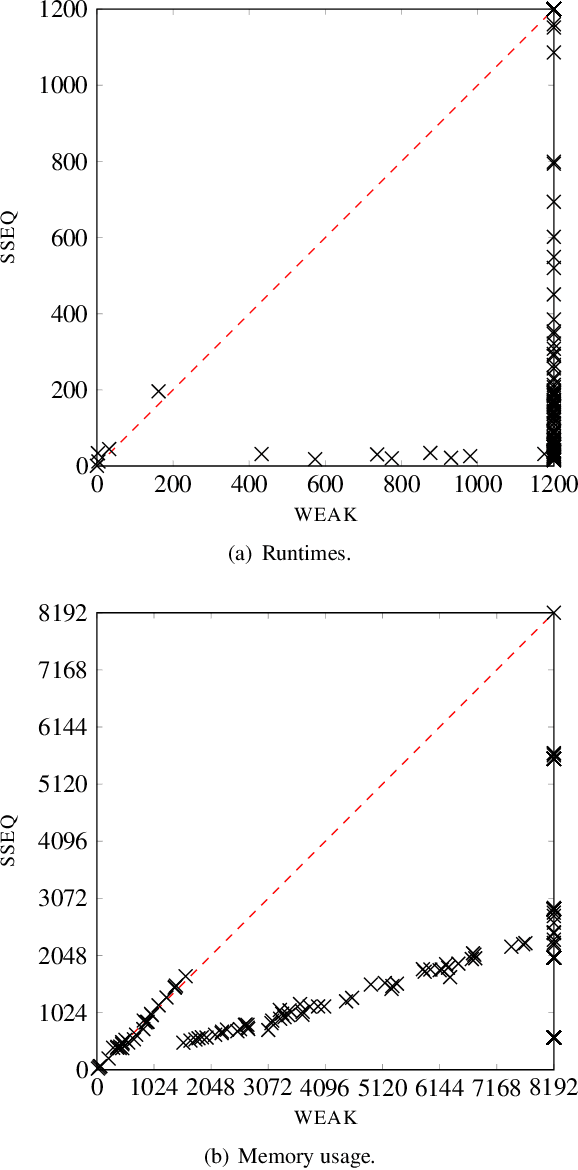
Abstract:Answer Set Programming (ASP) is a well-established formalism for logic programming. Problem solving in ASP requires to write an ASP program whose answers sets correspond to solutions. Albeit the non-existence of answer sets for some ASP programs can be considered as a modeling feature, it turns out to be a weakness in many other cases, and especially for query answering. Paracoherent answer set semantics extend the classical semantics of ASP to draw meaningful conclusions also from incoherent programs, with the result of increasing the range of applications of ASP. State of the art implementations of paracoherent ASP adopt the semi-equilibrium semantics, but cannot be lifted straightforwardly to compute efficiently the (better) split semi-equilibrium semantics that discards undesirable semi-equilibrium models. In this paper an efficient evaluation technique for computing a split semi-equilibrium model is presented. An experiment on hard benchmarks shows that better paracoherent answer sets can be computed consuming less computational resources than existing methods. Under consideration for acceptance in TPLP.
Beyond NP: Quantifying over Answer Sets
Jul 22, 2019Abstract:Answer Set Programming (ASP) is a logic programming paradigm featuring a purely declarative language with comparatively high modeling capabilities. Indeed, ASP can model problems in NP in a compact and elegant way. However, modeling problems beyond NP with ASP is known to be complicated, on the one hand, and limited to problems in {\Sigma}^P_2 on the other. Inspired by the way Quantified Boolean Formulas extend SAT formulas to model problems beyond NP, we propose an extension of ASP that introduces quantifiers over stable models of programs. We name the new language ASP with Quantifiers (ASP(Q)). In the paper we identify computational properties of ASP(Q); we highlight its modeling capabilities by reporting natural encodings of several complex problems with applications in artificial intelligence and number theory; and we compare ASP(Q) with related languages. Arguably, ASP(Q) allows one to model problems in the Polynomial Hierarchy in a direct way, providing an elegant expansion of ASP beyond the class NP. Under consideration for acceptance in TPLP.
Paracoherent Answer Set Semantics meets Argumentation Frameworks
Jul 22, 2019
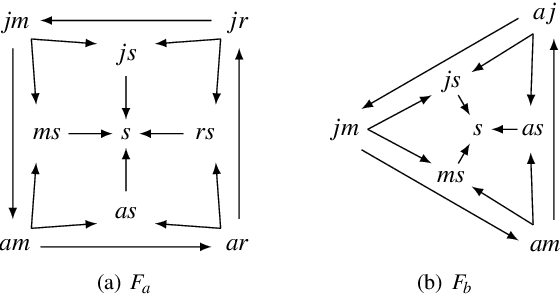
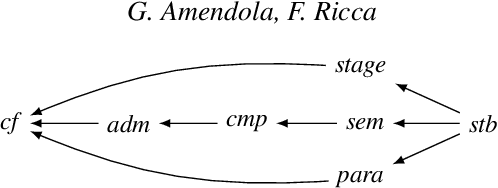
Abstract:In the last years, abstract argumentation has met with great success in AI, since it has served to capture several non-monotonic logics for AI. Relations between argumentation framework (AF) semantics and logic programming ones are investigating more and more. In particular, great attention has been given to the well-known stable extensions of an AF, that are closely related to the answer sets of a logic program. However, if a framework admits a small incoherent part, no stable extension can be provided. To overcome this shortcoming, two semantics generalizing stable extensions have been studied, namely semi-stable and stage. In this paper, we show that another perspective is possible on incoherent AFs, called paracoherent extensions, as they have a counterpart in paracoherent answer set semantics. We compare this perspective with semi-stable and stage semantics, by showing that computational costs remain unchanged, and moreover an interesting symmetric behaviour is maintained. Under consideration for acceptance in TPLP.
Abstract Solvers for Computing Cautious Consequences of ASP programs
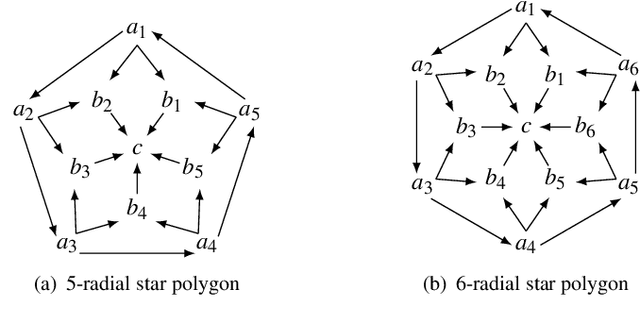
Jul 22, 2019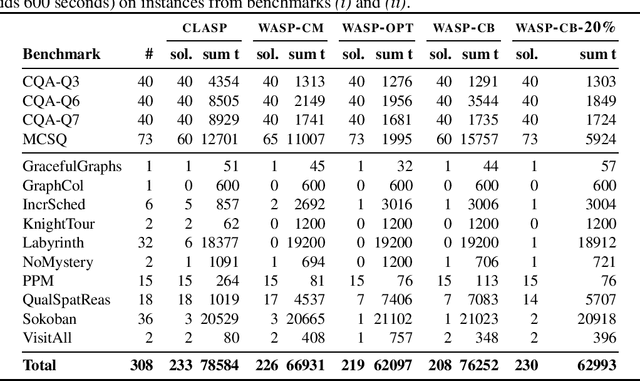



Abstract:Abstract solvers are a method to formally analyze algorithms that have been profitably used for describing, comparing and composing solving techniques in various fields such as Propositional Satisfiability (SAT), Quantified SAT, Satisfiability Modulo Theories, Answer Set Programming (ASP), and Constraint ASP. In this paper, we design, implement and test novel abstract solutions for cautious reasoning tasks in ASP. We show how to improve the current abstract solvers for cautious reasoning in ASP with new techniques borrowed from backbone computation in SAT, in order to design new solving algorithms. By doing so, we also formally show that the algorithms for solving cautious reasoning tasks in ASP are strongly related to those for computing backbones of Boolean formulas. We implement some of the new solutions in the ASP solver WASP and show that their performance are comparable to state-of-the-art solutions on the benchmark problems from the past ASP Competitions. Under consideration for acceptance in TPLP.
On the Computation of Paracoherent Answer Sets
Jul 21, 2017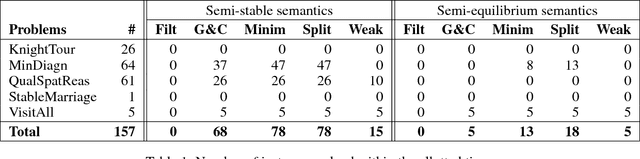
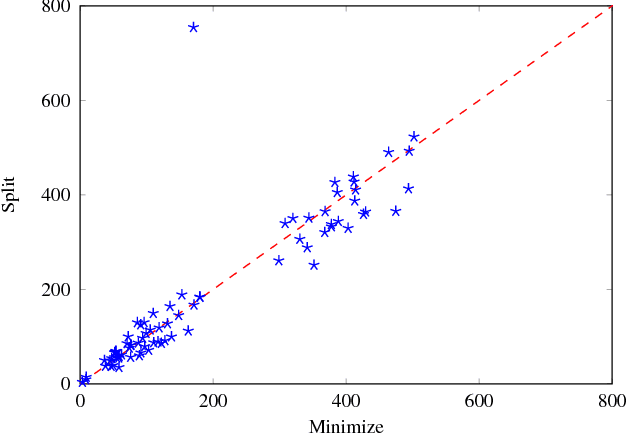
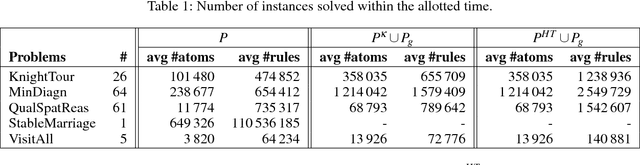
Abstract:Answer Set Programming (ASP) is a well-established formalism for nonmonotonic reasoning. An ASP program can have no answer set due to cyclic default negation. In this case, it is not possible to draw any conclusion, even if this is not intended. Recently, several paracoherent semantics have been proposed that address this issue, and several potential applications for these semantics have been identified. However, paracoherent semantics have essentially been inapplicable in practice, due to the lack of efficient algorithms and implementations. In this paper, this lack is addressed, and several different algorithms to compute semi-stable and semi-equilibrium models are proposed and implemented into an answer set solving framework. An empirical performance comparison among the new algorithms on benchmarks from ASP competitions is given as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge