Queries With Exact Truth Values in Paraconsistent Description Logics

We present a novel approach to querying classical inconsistent description logic (DL) knowledge bases by adopting a~paraconsistent semantics with the four Belnapian values: exactly true ($\mathbf{T}$), exactly false ($\mathbf{F}$), both ($\mathbf{B}$), and neither ($\mathbf{N}$). In contrast to prior studies on paraconsistent DLs, we allow truth value operators in the query language, which can be used to differentiate between answers having contradictory evidence and those having only positive evidence. We present a reduction to classical DL query answering that allows us to pinpoint the precise combined and data complexity of answering queries with values in paraconsistent $\mathcal{ALCHI}$ and its sublogics. Notably, we show that tractable data complexity is retained for Horn DLs. We present a comparison with repair-based inconsistency-tolerant semantics, showing that the two approaches are incomparable.

Knowledge Base Embeddings: Semantics and Theoretical Properties

Research on knowledge graph embeddings has recently evolved into knowledge base embeddings, where the goal is not only to map facts into vector spaces but also constrain the models so that they take into account the relevant conceptual knowledge available. This paper examines recent methods that have been proposed to embed knowledge bases in description logic into vector spaces through the lens of their geometric-based semantics. We identify several relevant theoretical properties, which we draw from the literature and sometimes generalize or unify. We then investigate how concrete embedding methods fit in this theoretical framework.

Cost-Based Semantics for Querying Inconsistent Weighted Knowledge Bases

In this paper, we explore a quantitative approach to querying inconsistent description logic knowledge bases. We consider weighted knowledge bases in which both axioms and assertions have (possibly infinite) weights, which are used to assign a cost to each interpretation based upon the axioms and assertions it violates. Two notions of certain and possible answer are defined by either considering interpretations whose cost does not exceed a given bound or restricting attention to optimal-cost interpretations. Our main contribution is a comprehensive analysis of the combined and data complexity of bounded cost satisfiability and certain and possible answer recognition, for description logics between ELbot and ALCO.

Semiring Provenance for Lightweight Description Logics

We investigate semiring provenance--a successful framework originally defined in the relational database setting--for description logics. In this context, the ontology axioms are annotated with elements of a commutative semiring and these annotations are propagated to the ontology consequences in a way that reflects how they are derived. We define a provenance semantics for a language that encompasses several lightweight description logics and show its relationships with semantics that have been defined for ontologies annotated with a specific kind of annotation (such as fuzzy degrees). We show that under some restrictions on the semiring, the semantics satisfies desirable properties (such as extending the semiring provenance defined for databases). We then focus on the well-known why-provenance, which allows to compute the semiring provenance for every additively and multiplicatively idempotent commutative semiring, and for which we study the complexity of problems related to the provenance of an axiom or a conjunctive query answer. Finally, we consider two more restricted cases which correspond to the so-called positive Boolean provenance and lineage in the database setting. For these cases, we exhibit relationships with well-known notions related to explanations in description logics and complete our complexity analysis. As a side contribution, we provide conditions on an ELHI_bot ontology that guarantee tractable reasoning.

Inconsistency Handling in Prioritized Databases with Universal Constraints: Complexity Analysis and Links with Active Integrity Constraints

This paper revisits the problem of repairing and querying inconsistent databases equipped with universal constraints. We adopt symmetric difference repairs, in which both deletions and additions of facts can be used to restore consistency, and suppose that preferred repair actions are specified via a binary priority relation over (negated) facts. Our first contribution is to show how existing notions of optimal repairs, defined for simpler denial constraints and repairs solely based on fact deletion, can be suitably extended to our richer setting. We next study the computational properties of the resulting repair notions, in particular, the data complexity of repair checking and inconsistency-tolerant query answering. Finally, we clarify the relationship between optimal repairs of prioritized databases and repair notions introduced in the framework of active integrity constraints. In particular, we show that Pareto-optimal repairs in our setting correspond to founded, grounded and justified repairs w.r.t. the active integrity constraints obtained by translating the prioritized database. Our study also yields useful insights into the behavior of active integrity constraints.

Querying Inconsistent Prioritized Data with ORBITS: Algorithms, Implementation, and Experiments

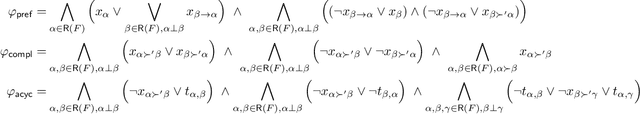
We investigate practical algorithms for inconsistency-tolerant query answering over prioritized knowledge bases, which consist of a logical theory, a set of facts, and a priority relation between conflicting facts. We consider three well-known semantics (AR, IAR and brave) based upon two notions of optimal repairs (Pareto and completion). Deciding whether a query answer holds under these semantics is (co)NP-complete in data complexity for a large class of logical theories, and SAT-based procedures have been devised for repair-based semantics when there is no priority relation, or the relation has a special structure. The present paper introduces the first SAT encodings for Pareto- and completion-optimal repairs w.r.t. general priority relations and proposes several ways of employing existing and new encodings to compute answers under (optimal) repair-based semantics, by exploiting different reasoning modes of SAT solvers. The comprehensive experimental evaluation of our implementation compares both (i) the impact of adopting semantics based on different kinds of repairs, and (ii) the relative performances of alternative procedures for the same semantics.

Geometric Models for (Temporally) Attributed Description Logics

In the search for knowledge graph embeddings that could capture ontological knowledge, geometric models of existential rules have been recently introduced. It has been shown that convex geometric regions capture the so-called quasi-chained rules. Attributed description logics (DL) have been defined to bridge the gap between DL languages and knowledge graphs, whose facts often come with various kinds of annotations that may need to be taken into account for reasoning. In particular, temporally attributed DLs are enriched by specific attributes whose semantics allows for some temporal reasoning. Considering that geometric models and (temporally) attributed DLs are promising tools designed for knowledge graphs, this paper investigates their compatibility, focusing on the attributed version of a Horn dialect of the DL-Lite family. We first adapt the definition of geometric models to attributed DLs and show that every satisfiable ontology has a convex geometric model. Our second contribution is a study of the impact of temporal attributes. We show that a temporally attributed DL may not have a convex geometric model in general but we can recover geometric satisfiability by imposing some restrictions on the use of the temporal attributes.

Querying and Repairing Inconsistent Prioritized Knowledge Bases: Complexity Analysis and Links with Abstract Argumentation

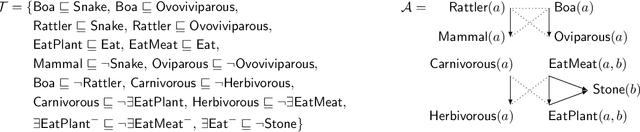
In this paper, we explore the issue of inconsistency handling over prioritized knowledge bases (KBs), which consist of an ontology, a set of facts, and a priority relation between conflicting facts. In the database setting, a closely related scenario has been studied and led to the definition of three different notions of optimal repairs (global, Pareto, and completion) of a prioritized inconsistent database. After transferring the notions of globally-, Pareto- and completion-optimal repairs to our setting, we study the data complexity of the core reasoning tasks: query entailment under inconsistency-tolerant semantics based upon optimal repairs, existence of a unique optimal repair, and enumeration of all optimal repairs. Our results provide a nearly complete picture of the data complexity of these tasks for ontologies formulated in common DL-Lite dialects. The second contribution of our work is to clarify the relationship between optimal repairs and different notions of extensions for (set-based) argumentation frameworks. Among our results, we show that Pareto-optimal repairs correspond precisely to stable extensions (and often also to preferred extensions), and we propose a novel semantics for prioritized KBs which is inspired by grounded extensions and enjoys favourable computational properties. Our study also yields some results of independent interest concerning preference-based argumentation frameworks.

Provenance for the Description Logic ELHr

We address the problem of handling provenance information in ELHr ontologies. We consider a setting recently introduced for ontology-based data access, based on semirings and extending classical data provenance, in which ontology axioms are annotated with provenance tokens. A consequence inherits the provenance of the axioms involved in deriving it, yielding a provenance polynomial as an annotation. We analyse the semantics for the ELHr case and show that the presence of conjunctions poses various difficulties for handling provenance, some of which are mitigated by assuming multiplicative idempotency of the semiring. Under this assumption, we study three problems: ontology completion with provenance, computing the set of relevant axioms for a consequence, and query answering.