On the Power and Limitations of Examples for Description Logic Concepts

Labeled examples (i.e., positive and negative examples) are an attractive medium for communicating complex concepts. They are useful for deriving concept expressions (such as in concept learning, interactive concept specification, and concept refinement) as well as for illustrating concept expressions to a user or domain expert. We investigate the power of labeled examples for describing description-logic concepts. Specifically, we systematically study the existence and efficient computability of finite characterisations, i.e. finite sets of labeled examples that uniquely characterize a single concept, for a wide variety of description logics between EL and ALCQI, both without an ontology and in the presence of a DL-Lite ontology. Finite characterisations are relevant for debugging purposes, and their existence is a necessary condition for exact learnability with membership queries.

Knowledge Base Embeddings: Semantics and Theoretical Properties

Research on knowledge graph embeddings has recently evolved into knowledge base embeddings, where the goal is not only to map facts into vector spaces but also constrain the models so that they take into account the relevant conceptual knowledge available. This paper examines recent methods that have been proposed to embed knowledge bases in description logic into vector spaces through the lens of their geometric-based semantics. We identify several relevant theoretical properties, which we draw from the literature and sometimes generalize or unify. We then investigate how concrete embedding methods fit in this theoretical framework.

Learning Horn Envelopes via Queries from Large Language Models

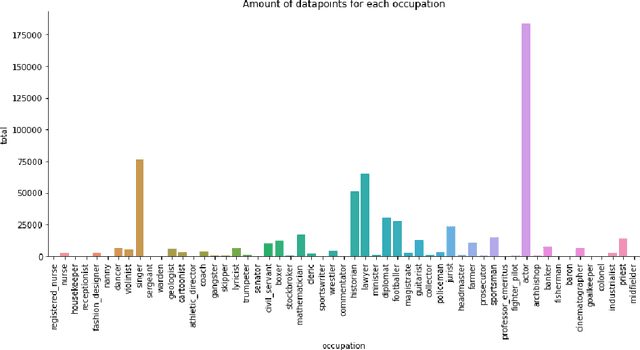
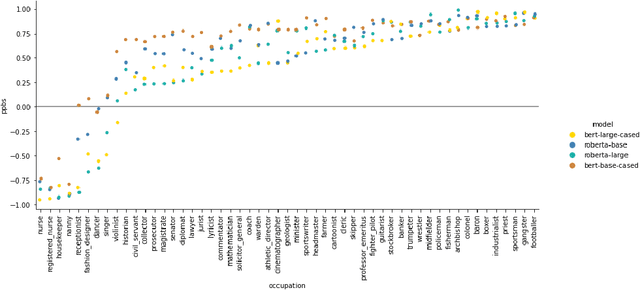
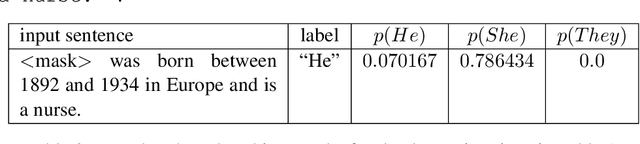
We investigate an approach for extracting knowledge from trained neural networks based on Angluin's exact learning model with membership and equivalence queries to an oracle. In this approach, the oracle is a trained neural network. We consider Angluin's classical algorithm for learning Horn theories and study the necessary changes to make it applicable to learn from neural networks. In particular, we have to consider that trained neural networks may not behave as Horn oracles, meaning that their underlying target theory may not be Horn. We propose a new algorithm that aims at extracting the ``tightest Horn approximation'' of the target theory and that is guaranteed to terminate in exponential time (in the worst case) and in polynomial time if the target has polynomially many non-Horn examples. To showcase the applicability of the approach, we perform experiments on pre-trained language models and extract rules that expose occupation-based gender biases.