Escaping Plato's Cave: Towards the Alignment of 3D and Text Latent Spaces

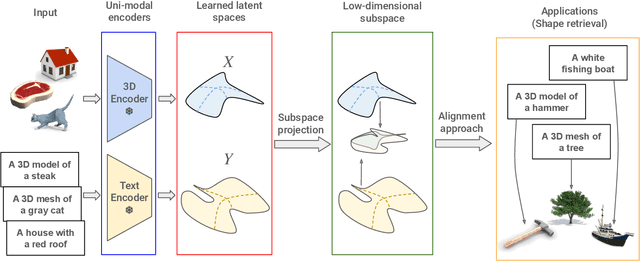
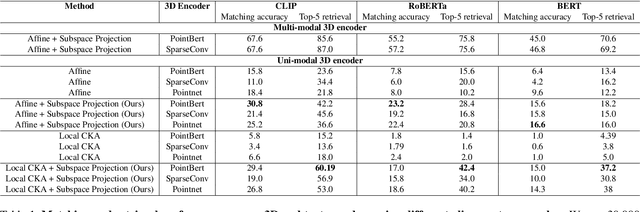
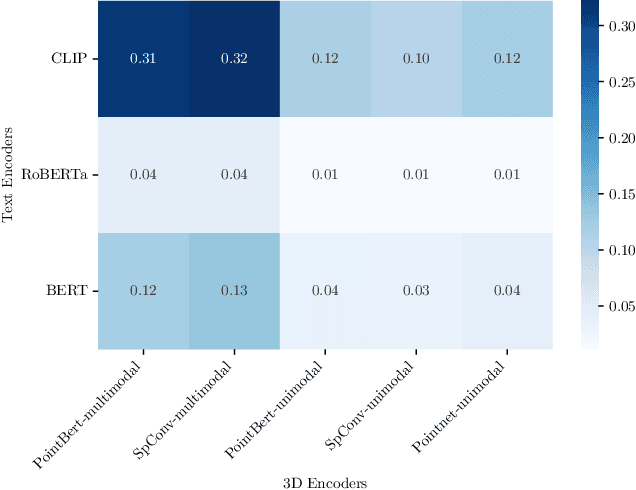
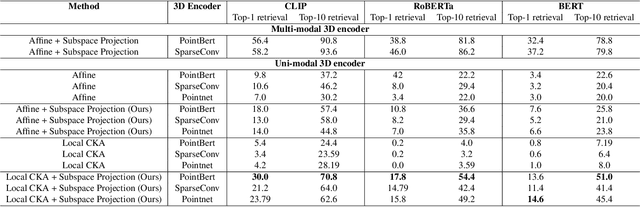
Recent works have shown that, when trained at scale, uni-modal 2D vision and text encoders converge to learned features that share remarkable structural properties, despite arising from different representations. However, the role of 3D encoders with respect to other modalities remains unexplored. Furthermore, existing 3D foundation models that leverage large datasets are typically trained with explicit alignment objectives with respect to frozen encoders from other representations. In this work, we investigate the possibility of a posteriori alignment of representations obtained from uni-modal 3D encoders compared to text-based feature spaces. We show that naive post-training feature alignment of uni-modal text and 3D encoders results in limited performance. We then focus on extracting subspaces of the corresponding feature spaces and discover that by projecting learned representations onto well-chosen lower-dimensional subspaces the quality of alignment becomes significantly higher, leading to improved accuracy on matching and retrieval tasks. Our analysis further sheds light on the nature of these shared subspaces, which roughly separate between semantic and geometric data representations. Overall, ours is the first work that helps to establish a baseline for post-training alignment of 3D uni-modal and text feature spaces, and helps to highlight both the shared and unique properties of 3D data compared to other representations.

How to Blend Concepts in Diffusion Models

For the last decade, there has been a push to use multi-dimensional (latent) spaces to represent concepts; and yet how to manipulate these concepts or reason with them remains largely unclear. Some recent methods exploit multiple latent representations and their connection, making this research question even more entangled. Our goal is to understand how operations in the latent space affect the underlying concepts. To that end, we explore the task of concept blending through diffusion models. Diffusion models are based on a connection between a latent representation of textual prompts and a latent space that enables image reconstruction and generation. This task allows us to try different text-based combination strategies, and evaluate easily through a visual analysis. Our conclusion is that concept blending through space manipulation is possible, although the best strategy depends on the context of the blend.

Implicit-ARAP: Efficient Handle-Guided Deformation of High-Resolution Meshes and Neural Fields via Local Patch Meshing

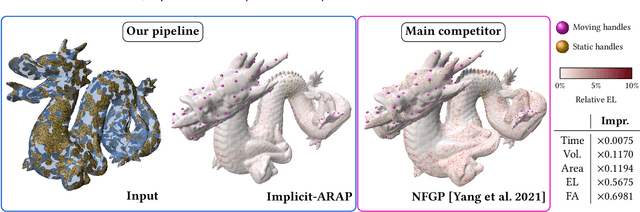
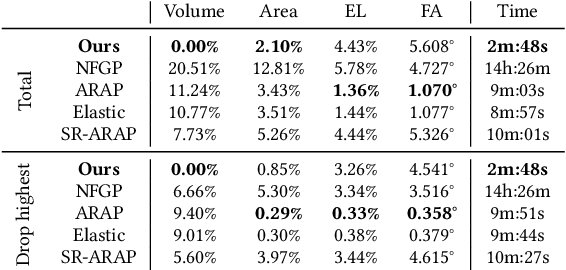
In this work, we present the local patch mesh representation for neural signed distance fields. This technique allows to discretize local regions of the level sets of an input SDF by projecting and deforming flat patch meshes onto the level set surface, using exclusively the SDF information and its gradient. Our analysis reveals this method to be more accurate than the standard marching cubes algorithm for approximating the implicit surface. Then, we apply this representation in the setting of handle-guided deformation: we introduce two distinct pipelines, which make use of 3D neural fields to compute As-Rigid-As-Possible deformations of both high-resolution meshes and neural fields under a given set of constraints. We run a comprehensive evaluation of our method and various baselines for neural field and mesh deformation which show both pipelines achieve impressive efficiency and notable improvements in terms of quality of results and robustness. With our novel pipeline, we introduce a scalable approach to solve a well-established geometry processing problem on high-resolution meshes, and pave the way for extending other geometric tasks to the domain of implicit surfaces via local patch meshing.

Disentangled Latent Spaces Facilitate Data-Driven Auxiliary Learning

In deep learning, auxiliary objectives are often used to facilitate learning in situations where data is scarce, or the principal task is extremely complex. This idea is primarily inspired by the improved generalization capability induced by solving multiple tasks simultaneously, which leads to a more robust shared representation. Nevertheless, finding optimal auxiliary tasks that give rise to the desired improvement is a crucial problem that often requires hand-crafted solutions or expensive meta-learning approaches. In this paper, we propose a novel framework, dubbed Detaux, whereby a weakly supervised disentanglement procedure is used to discover new unrelated classification tasks and the associated labels that can be exploited with the principal task in any Multi-Task Learning (MTL) model. The disentanglement procedure works at a representation level, isolating a subspace related to the principal task, plus an arbitrary number of orthogonal subspaces. In the most disentangled subspaces, through a clustering procedure, we generate the additional classification tasks, and the associated labels become their representatives. Subsequently, the original data, the labels associated with the principal task, and the newly discovered ones can be fed into any MTL framework. Extensive validation on both synthetic and real data, along with various ablation studies, demonstrate promising results, revealing the potential in what has been, so far, an unexplored connection between learning disentangled representations and MTL. The code will be made publicly available upon acceptance.

Extracting a functional representation from a dictionary for non-rigid shape matching

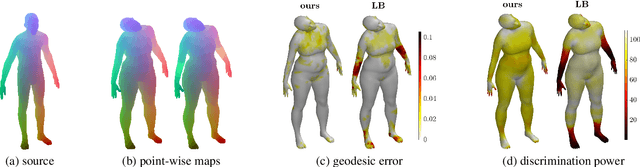
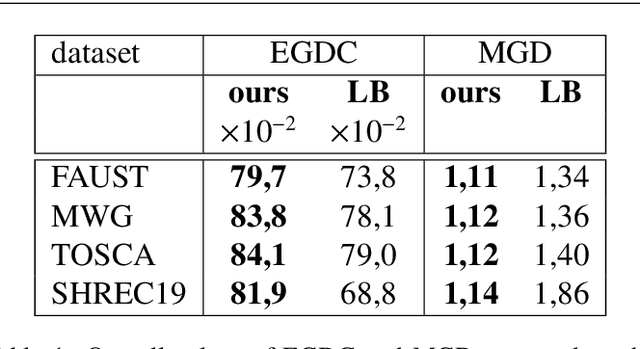
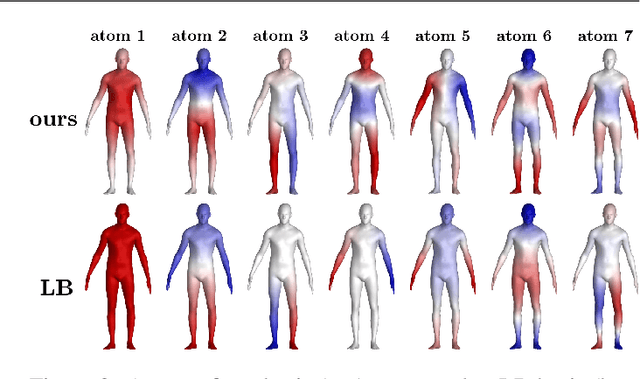
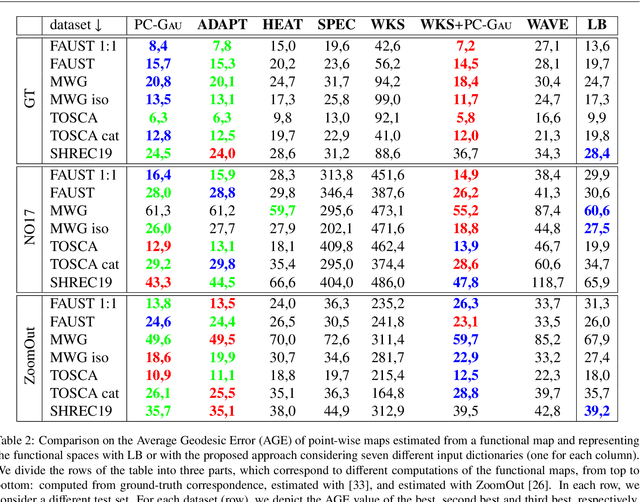
Shape matching is a fundamental problem in computer graphics with many applications. Functional maps translate the point-wise shape-matching problem into its functional counterpart and have inspired numerous solutions over the last decade. Nearly all the solutions based on functional maps rely on the eigenfunctions of the Laplace-Beltrami Operator (LB) to describe the functional spaces defined on the surfaces and then convert the functional correspondences into point-wise correspondences. However, this final step is often error-prone and inaccurate in tiny regions and protrusions, where the energy of LB does not uniformly cover the surface. We propose a new functional basis Principal Components of a Dictionary (PCD) to address such intrinsic limitation. PCD constructs an orthonormal basis from the Principal Component Analysis (PCA) of a dictionary of functions defined over the shape. These dictionaries can target specific properties of the final basis, such as achieving an even spreading of energy. Our experimental evaluation compares seven different dictionaries on established benchmarks, showing that PCD is suited to target different shape-matching scenarios, resulting in more accurate point-wise maps than the LB basis when used in the same pipeline. This evidence provides a promising alternative for improving correspondence estimation, confirming the power and flexibility of functional maps.

Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models

Language models demonstrate both quantitative improvement and new qualitative capabilities with increasing scale. Despite their potentially transformative impact, these new capabilities are as yet poorly characterized. In order to inform future research, prepare for disruptive new model capabilities, and ameliorate socially harmful effects, it is vital that we understand the present and near-future capabilities and limitations of language models. To address this challenge, we introduce the Beyond the Imitation Game benchmark (BIG-bench). BIG-bench currently consists of 204 tasks, contributed by 442 authors across 132 institutions. Task topics are diverse, drawing problems from linguistics, childhood development, math, common-sense reasoning, biology, physics, social bias, software development, and beyond. BIG-bench focuses on tasks that are believed to be beyond the capabilities of current language models. We evaluate the behavior of OpenAI's GPT models, Google-internal dense transformer architectures, and Switch-style sparse transformers on BIG-bench, across model sizes spanning millions to hundreds of billions of parameters. In addition, a team of human expert raters performed all tasks in order to provide a strong baseline. Findings include: model performance and calibration both improve with scale, but are poor in absolute terms (and when compared with rater performance); performance is remarkably similar across model classes, though with benefits from sparsity; tasks that improve gradually and predictably commonly involve a large knowledge or memorization component, whereas tasks that exhibit "breakthrough" behavior at a critical scale often involve multiple steps or components, or brittle metrics; social bias typically increases with scale in settings with ambiguous context, but this can be improved with prompting.

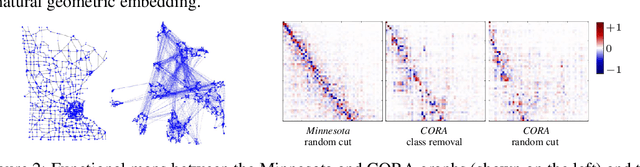
Harnessing spectral representations for subgraph alignment

With the rise and advent of graph learning techniques, graph data has become ubiquitous. However, while several efforts are being devoted to the design of new convolutional architectures, pooling or positional encoding schemes, less effort is being spent on problems involving maps between (possibly very large) graphs, such as signal transfer, graph isomorphism and subgraph correspondence. With this paper, we anticipate the need for a convenient framework to deal with such problems, and focus in particular on the challenging subgraph alignment scenario. We claim that, first and foremost, the representation of a map plays a central role on how these problems should be modeled. Taking the hint from recent work in geometry processing, we propose the adoption of a spectral representation for maps that is compact, easy to compute, robust to topological changes, easy to plug into existing pipelines, and is especially effective for subgraph alignment problems. We report for the first time a surprising phenomenon where the partiality arising in the subgraph alignment task is manifested as a special structure of the map coefficients, even in the absence of exact subgraph isomorphism, and which is consistently observed over different families of graphs up to several thousand nodes.

Explanatory Learning: Beyond Empiricism in Neural Networks

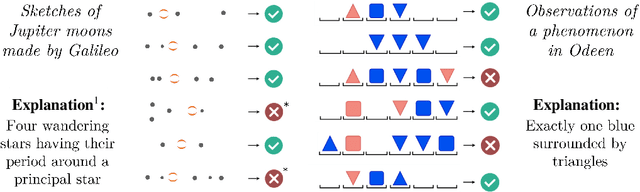
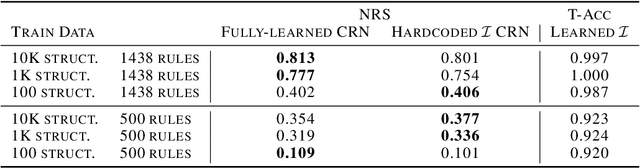
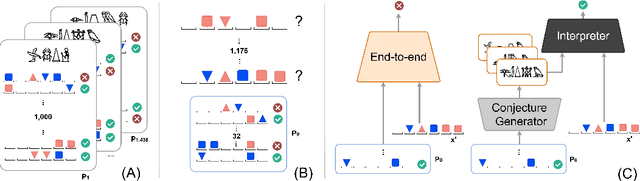
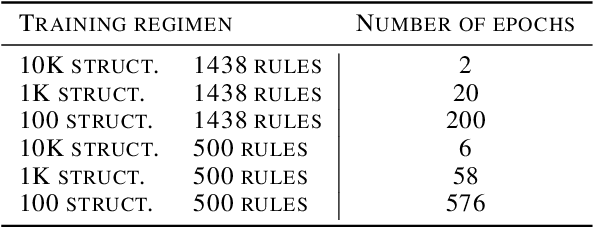
We introduce Explanatory Learning (EL), a framework to let machines use existing knowledge buried in symbolic sequences -- e.g. explanations written in hieroglyphic -- by autonomously learning to interpret them. In EL, the burden of interpreting symbols is not left to humans or rigid human-coded compilers, as done in Program Synthesis. Rather, EL calls for a learned interpreter, built upon a limited collection of symbolic sequences paired with observations of several phenomena. This interpreter can be used to make predictions on a novel phenomenon given its explanation, and even to find that explanation using only a handful of observations, like human scientists do. We formulate the EL problem as a simple binary classification task, so that common end-to-end approaches aligned with the dominant empiricist view of machine learning could, in principle, solve it. To these models, we oppose Critical Rationalist Networks (CRNs), which instead embrace a rationalist view on the acquisition of knowledge. CRNs express several desired properties by construction, they are truly explainable, can adjust their processing at test-time for harder inferences, and can offer strong confidence guarantees on their predictions. As a final contribution, we introduce Odeen, a basic EL environment that simulates a small flatland-style universe full of phenomena to explain. Using Odeen as a testbed, we show how CRNs outperform empiricist end-to-end approaches of similar size and architecture (Transformers) in discovering explanations for novel phenomena.

Complex Functional Maps : a Conformal Link Between Tangent Bundles

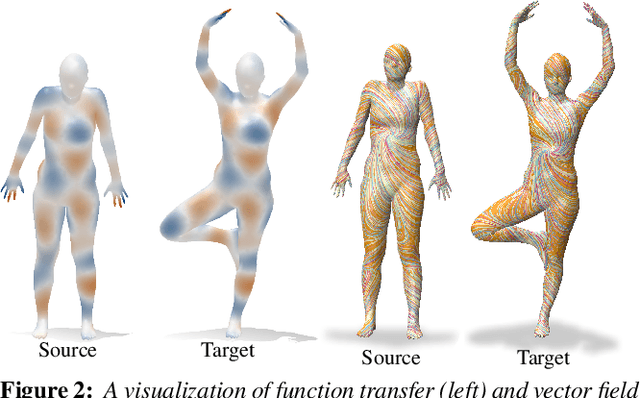
In this paper, we introduce complex functional maps, which extend the functional map framework to conformal maps between tangent vector fields on surfaces. A key property of these maps is their orientation awareness. More specifically, we demonstrate that unlike regular functional maps that link functional spaces of two manifolds, our complex functional maps establish a link between oriented tangent bundles, thus permitting robust and efficient transfer of tangent vector fields. By first endowing and then exploiting the tangent bundle of each shape with a complex structure, the resulting operations become naturally orientationaware, thus favoring orientation and angle preserving correspondence across shapes, without relying on descriptors or extra regularization. Finally, and perhaps more importantly, we demonstrate how these objects enable several practical applications within the functional map framework. We show that functional maps and their complex counterparts can be estimated jointly to promote orientation preservation, regularizing pipelines that previously suffered from orientation-reversing symmetry errors.

Why you should learn functional basis

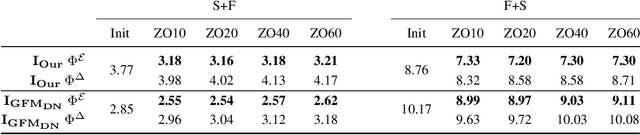
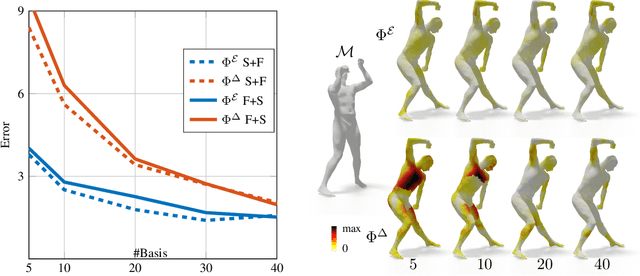
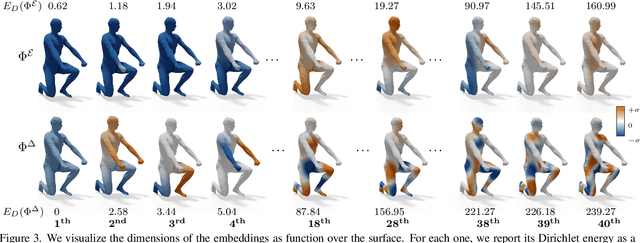
Efficient and practical representation of geometric data is a ubiquitous problem for several applications in geometry processing. A widely used choice is to encode the 3D objects through their spectral embedding, associating to each surface point the values assumed at that point by a truncated subset of the eigenfunctions of a differential operator (typically the Laplacian). Several attempts to define new, preferable embeddings for different applications have seen the light during the last decade. Still, the standard Laplacian eigenfunctions remain solidly at the top of the available solutions, despite their limitations, such as being limited to near-isometries for shape matching. Recently, a new trend shows advantages in learning substitutes for the Laplacian eigenfunctions. At the same time, many research questions remain unsolved: are the new bases better than the LBO eigenfunctions, and how do they relate to them? How do they act in the functional perspective? And how to exploit these bases in new configurations in conjunction with additional features and descriptors? In this study, we properly pose these questions to improve our understanding of this emerging research direction. We show their applicative relevance in different contexts revealing some of their insights and exciting future directions.