3D-WAG: Hierarchical Wavelet-Guided Autoregressive Generation for High-Fidelity 3D Shapes

Autoregressive (AR) models have achieved remarkable success in natural language and image generation, but their application to 3D shape modeling remains largely unexplored. Unlike diffusion models, AR models enable more efficient and controllable generation with faster inference times, making them especially suitable for data-intensive domains. Traditional 3D generative models using AR approaches often rely on ``next-token" predictions at the voxel or point level. While effective for certain applications, these methods can be restrictive and computationally expensive when dealing with large-scale 3D data. To tackle these challenges, we introduce 3D-WAG, an AR model for 3D implicit distance fields that can perform unconditional shape generation, class-conditioned and also text-conditioned shape generation. Our key idea is to encode shapes as multi-scale wavelet token maps and use a Transformer to predict the ``next higher-resolution token map" in an autoregressive manner. By redefining 3D AR generation task as ``next-scale" prediction, we reduce the computational cost of generation compared to traditional ``next-token" prediction models, while preserving essential geometric details of 3D shapes in a more structured and hierarchical manner. We evaluate 3D-WAG to showcase its benefit by quantitative and qualitative comparisons with state-of-the-art methods on widely used benchmarks. Our results show 3D-WAG achieves superior performance in key metrics like Coverage and MMD, generating high-fidelity 3D shapes that closely match the real data distribution.

Wavelet Latent Diffusion (Wala): Billion-Parameter 3D Generative Model with Compact Wavelet Encodings

Large-scale 3D generative models require substantial computational resources yet often fall short in capturing fine details and complex geometries at high resolutions. We attribute this limitation to the inefficiency of current representations, which lack the compactness required to model the generative models effectively. To address this, we introduce a novel approach called Wavelet Latent Diffusion, or WaLa, that encodes 3D shapes into wavelet-based, compact latent encodings. Specifically, we compress a $256^3$ signed distance field into a $12^3 \times 4$ latent grid, achieving an impressive 2427x compression ratio with minimal loss of detail. This high level of compression allows our method to efficiently train large-scale generative networks without increasing the inference time. Our models, both conditional and unconditional, contain approximately one billion parameters and successfully generate high-quality 3D shapes at $256^3$ resolution. Moreover, WaLa offers rapid inference, producing shapes within two to four seconds depending on the condition, despite the model's scale. We demonstrate state-of-the-art performance across multiple datasets, with significant improvements in generation quality, diversity, and computational efficiency. We open-source our code and, to the best of our knowledge, release the largest pretrained 3D generative models across different modalities.

Make-A-Shape: a Ten-Million-scale 3D Shape Model

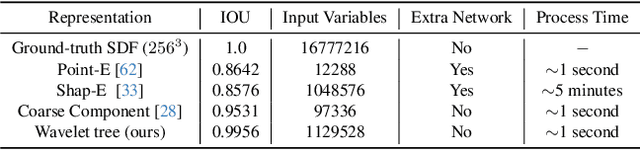
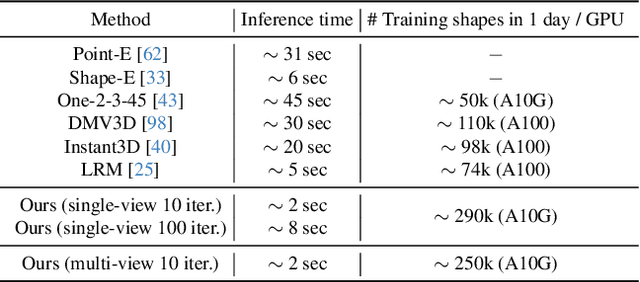
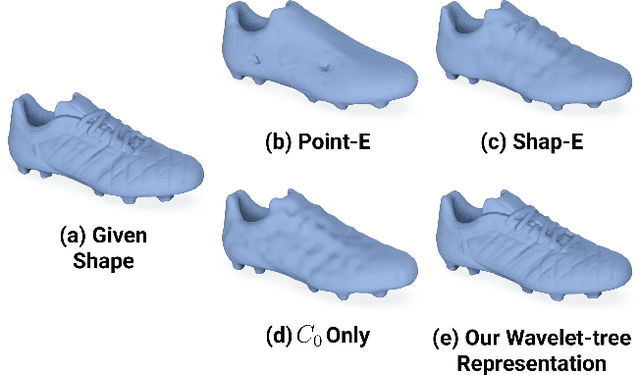
Significant progress has been made in training large generative models for natural language and images. Yet, the advancement of 3D generative models is hindered by their substantial resource demands for training, along with inefficient, non-compact, and less expressive representations. This paper introduces Make-A-Shape, a new 3D generative model designed for efficient training on a vast scale, capable of utilizing 10 millions publicly-available shapes. Technical-wise, we first innovate a wavelet-tree representation to compactly encode shapes by formulating the subband coefficient filtering scheme to efficiently exploit coefficient relations. We then make the representation generatable by a diffusion model by devising the subband coefficients packing scheme to layout the representation in a low-resolution grid. Further, we derive the subband adaptive training strategy to train our model to effectively learn to generate coarse and detail wavelet coefficients. Last, we extend our framework to be controlled by additional input conditions to enable it to generate shapes from assorted modalities, e.g., single/multi-view images, point clouds, and low-resolution voxels. In our extensive set of experiments, we demonstrate various applications, such as unconditional generation, shape completion, and conditional generation on a wide range of modalities. Our approach not only surpasses the state of the art in delivering high-quality results but also efficiently generates shapes within a few seconds, often achieving this in just 2 seconds for most conditions.

Sketch-A-Shape: Zero-Shot Sketch-to-3D Shape Generation

Significant progress has recently been made in creative applications of large pre-trained models for downstream tasks in 3D vision, such as text-to-shape generation. This motivates our investigation of how these pre-trained models can be used effectively to generate 3D shapes from sketches, which has largely remained an open challenge due to the limited sketch-shape paired datasets and the varying level of abstraction in the sketches. We discover that conditioning a 3D generative model on the features (obtained from a frozen large pre-trained vision model) of synthetic renderings during training enables us to effectively generate 3D shapes from sketches at inference time. This suggests that the large pre-trained vision model features carry semantic signals that are resilient to domain shifts, i.e., allowing us to use only RGB renderings, but generalizing to sketches at inference time. We conduct a comprehensive set of experiments investigating different design factors and demonstrate the effectiveness of our straightforward approach for generation of multiple 3D shapes per each input sketch regardless of their level of abstraction without requiring any paired datasets during training.

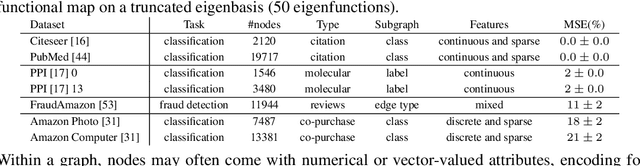
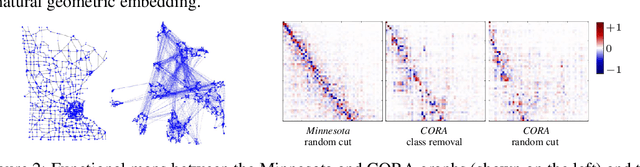
Harnessing spectral representations for subgraph alignment

With the rise and advent of graph learning techniques, graph data has become ubiquitous. However, while several efforts are being devoted to the design of new convolutional architectures, pooling or positional encoding schemes, less effort is being spent on problems involving maps between (possibly very large) graphs, such as signal transfer, graph isomorphism and subgraph correspondence. With this paper, we anticipate the need for a convenient framework to deal with such problems, and focus in particular on the challenging subgraph alignment scenario. We claim that, first and foremost, the representation of a map plays a central role on how these problems should be modeled. Taking the hint from recent work in geometry processing, we propose the adoption of a spectral representation for maps that is compact, easy to compute, robust to topological changes, easy to plug into existing pipelines, and is especially effective for subgraph alignment problems. We report for the first time a surprising phenomenon where the partiality arising in the subgraph alignment task is manifested as a special structure of the map coefficients, even in the absence of exact subgraph isomorphism, and which is consistently observed over different families of graphs up to several thousand nodes.

Universal Spectral Adversarial Attacks for Deformable Shapes

Machine learning models are known to be vulnerable to adversarial attacks, namely perturbations of the data that lead to wrong predictions despite being imperceptible. However, the existence of "universal" attacks (i.e., unique perturbations that transfer across different data points) has only been demonstrated for images to date. Part of the reason lies in the lack of a common domain, for geometric data such as graphs, meshes, and point clouds, where a universal perturbation can be defined. In this paper, we offer a change in perspective and demonstrate the existence of universal attacks for geometric data (shapes). We introduce a computational procedure that operates entirely in the spectral domain, where the attacks take the form of small perturbations to short eigenvalue sequences; the resulting geometry is then synthesized via shape-from-spectrum recovery. Our attacks are universal, in that they transfer across different shapes, different representations (meshes and point clouds), and generalize to previously unseen data.

Instant recovery of shape from spectrum via latent space connections

We introduce the first learning-based method for recovering shapes from Laplacian spectra. Given an auto-encoder, our model takes the form of a cycle-consistent module to map latent vectors to sequences of eigenvalues. This module provides an efficient and effective linkage between spectrum and geometry of a given shape. Our data-driven approach replaces the need for ad-hoc regularizers required by prior methods, while providing more accurate results at a fraction of the computational cost. Our learning model applies without modifications across different dimensions (2D and 3D shapes alike), representations (meshes, contours and point clouds), as well as across different shape classes, and admits arbitrary resolution of the input spectrum without affecting complexity. The increased flexibility allows us to provide a proxy to differentiable eigendecomposition and to address notoriously difficult tasks in 3D vision and geometry processing within a unified framework, including shape generation from spectrum, mesh super-resolution, shape exploration, style transfer, spectrum estimation from point clouds, segmentation transfer and point-to-point matching.

Isospectralization, or how to hear shape, style, and correspondence

The question whether one can recover the shape of a geometric object from its Laplacian spectrum (`hear the shape of the drum') is a classical problem in spectral geometry with a broad range of implications and applications. While theoretically the answer to this question is negative (there exist examples of iso-spectral but non-isometric manifolds), little is known about the practical possibility of using the spectrum for shape reconstruction and optimization. In this paper, we introduce a numerical procedure called {\em isospectralization}, consisting of deforming one shape to make its Laplacian spectrum match that of another. We implement the isospectralization procedure using modern differentiable programming techniques and exemplify its applications in some of the classical and notoriously hard problems in geometry processing, computer vision, and graphics such as shape reconstruction, pose and style transfer, and dense deformable correspondence.