Learning Multi-resolution Functional Maps with Spectral Attention for Robust Shape Matching

In this work, we present a novel non-rigid shape matching framework based on multi-resolution functional maps with spectral attention. Existing functional map learning methods all rely on the critical choice of the spectral resolution hyperparameter, which can severely affect the overall accuracy or lead to overfitting, if not chosen carefully. In this paper, we show that spectral resolution tuning can be alleviated by introducing spectral attention. Our framework is applicable in both supervised and unsupervised settings, and we show that it is possible to train the network so that it can adapt the spectral resolution, depending on the given shape input. More specifically, we propose to compute multi-resolution functional maps that characterize correspondence across a range of spectral resolutions, and introduce a spectral attention network that helps to combine this representation into a single coherent final correspondence. Our approach is not only accurate with near-isometric input, for which a high spectral resolution is typically preferred, but also robust and able to produce reasonable matching even in the presence of significant non-isometric distortion, which poses great challenges to existing methods. We demonstrate the superior performance of our approach through experiments on a suite of challenging near-isometric and non-isometric shape matching benchmarks.

Deep Orientation-Aware Functional Maps: Tackling Symmetry Issues in Shape Matching

State-of-the-art fully intrinsic networks for non-rigid shape matching often struggle to disambiguate the symmetries of the shapes leading to unstable correspondence predictions. Meanwhile, recent advances in the functional map framework allow to enforce orientation preservation using a functional representation for tangent vector field transfer, through so-called complex functional maps. Using this representation, we propose a new deep learning approach to learn orientation-aware features in a fully unsupervised setting. Our architecture is built on top of DiffusionNet, making it robust to discretization changes. Additionally, we introduce a vector field-based loss, which promotes orientation preservation without using (often unstable) extrinsic descriptors.

Complex Functional Maps : a Conformal Link Between Tangent Bundles

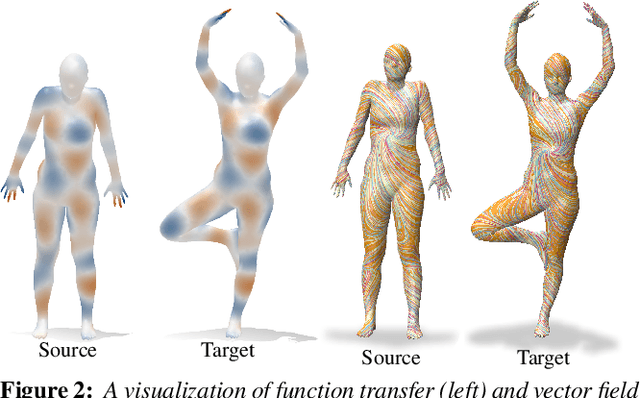
In this paper, we introduce complex functional maps, which extend the functional map framework to conformal maps between tangent vector fields on surfaces. A key property of these maps is their orientation awareness. More specifically, we demonstrate that unlike regular functional maps that link functional spaces of two manifolds, our complex functional maps establish a link between oriented tangent bundles, thus permitting robust and efficient transfer of tangent vector fields. By first endowing and then exploiting the tangent bundle of each shape with a complex structure, the resulting operations become naturally orientationaware, thus favoring orientation and angle preserving correspondence across shapes, without relying on descriptors or extra regularization. Finally, and perhaps more importantly, we demonstrate how these objects enable several practical applications within the functional map framework. We show that functional maps and their complex counterparts can be estimated jointly to promote orientation preservation, regularizing pipelines that previously suffered from orientation-reversing symmetry errors.

Deep Geometric Functional Maps: Robust Feature Learning for Shape Correspondence

We present a novel learning-based approach for computing correspondences between non-rigid 3D shapes. Unlike previous methods that either require extensive training data or operate on handcrafted input descriptors and thus generalize poorly across diverse datasets, our approach is both accurate and robust to changes in shape structure. Key to our method is a feature-extraction network that learns directly from raw shape geometry, combined with a novel regularized map extraction layer and loss, based on the functional map representation. We demonstrate through extensive experiments in challenging shape matching scenarios that our method can learn from less training data than existing supervised approaches and generalizes significantly better than current descriptor-based learning methods. Our source code is available at: https://github.com/LIX-shape-analysis/GeomFmaps.