Deep Orientation-Aware Functional Maps: Tackling Symmetry Issues in Shape Matching

State-of-the-art fully intrinsic networks for non-rigid shape matching often struggle to disambiguate the symmetries of the shapes leading to unstable correspondence predictions. Meanwhile, recent advances in the functional map framework allow to enforce orientation preservation using a functional representation for tangent vector field transfer, through so-called complex functional maps. Using this representation, we propose a new deep learning approach to learn orientation-aware features in a fully unsupervised setting. Our architecture is built on top of DiffusionNet, making it robust to discretization changes. Additionally, we introduce a vector field-based loss, which promotes orientation preservation without using (often unstable) extrinsic descriptors.

Complex Functional Maps : a Conformal Link Between Tangent Bundles

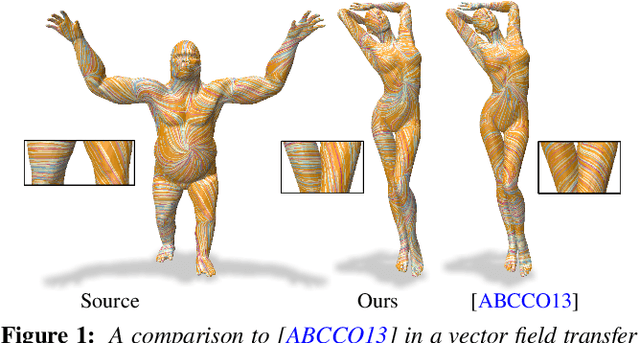
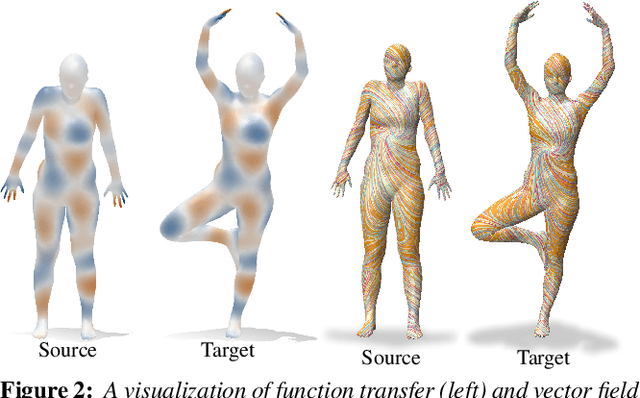
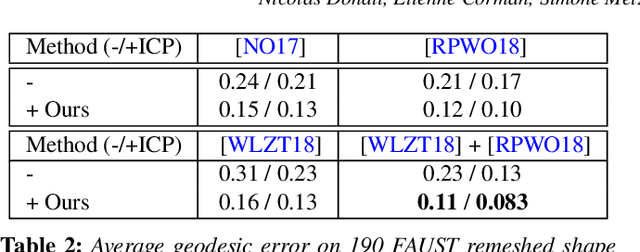
In this paper, we introduce complex functional maps, which extend the functional map framework to conformal maps between tangent vector fields on surfaces. A key property of these maps is their orientation awareness. More specifically, we demonstrate that unlike regular functional maps that link functional spaces of two manifolds, our complex functional maps establish a link between oriented tangent bundles, thus permitting robust and efficient transfer of tangent vector fields. By first endowing and then exploiting the tangent bundle of each shape with a complex structure, the resulting operations become naturally orientationaware, thus favoring orientation and angle preserving correspondence across shapes, without relying on descriptors or extra regularization. Finally, and perhaps more importantly, we demonstrate how these objects enable several practical applications within the functional map framework. We show that functional maps and their complex counterparts can be estimated jointly to promote orientation preservation, regularizing pipelines that previously suffered from orientation-reversing symmetry errors.