Shape Non-rigid Kinematics : A Zero-Shot Method for Non-Rigid Shape Matching via Unsupervised Functional Map Regularized Reconstruction

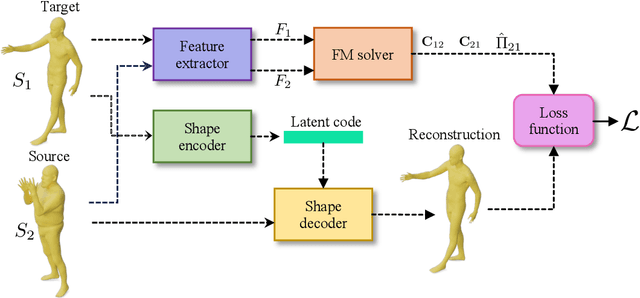
We present Shape Non-rigid Kinematics (SNK), a novel zero-shot method for non-rigid shape matching that eliminates the need for extensive training or ground truth data. SNK operates on a single pair of shapes, and employs a reconstruction-based strategy using an encoder-decoder architecture, which deforms the source shape to closely match the target shape. During the process, an unsupervised functional map is predicted and converted into a point-to-point map, serving as a supervisory mechanism for the reconstruction. To aid in training, we have designed a new decoder architecture that generates smooth, realistic deformations. SNK demonstrates competitive results on traditional benchmarks, simplifying the shape-matching process without compromising accuracy. Our code can be found online: https://github.com/pvnieo/SNK

Unsupervised Representation Learning for Diverse Deformable Shape Collections

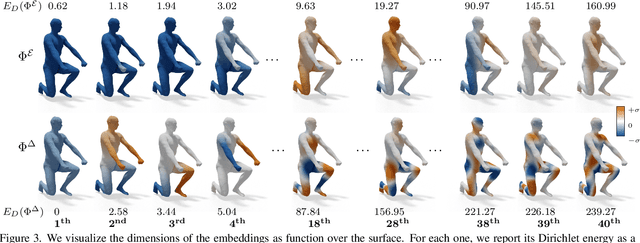
We introduce a novel learning-based method for encoding and manipulating 3D surface meshes. Our method is specifically designed to create an interpretable embedding space for deformable shape collections. Unlike previous 3D mesh autoencoders that require meshes to be in a 1-to-1 correspondence, our approach is trained on diverse meshes in an unsupervised manner. Central to our method is a spectral pooling technique that establishes a universal latent space, breaking free from traditional constraints of mesh connectivity and shape categories. The entire process consists of two stages. In the first stage, we employ the functional map paradigm to extract point-to-point (p2p) maps between a collection of shapes in an unsupervised manner. These p2p maps are then utilized to construct a common latent space, which ensures straightforward interpretation and independence from mesh connectivity and shape category. Through extensive experiments, we demonstrate that our method achieves excellent reconstructions and produces more realistic and smoother interpolations than baseline approaches.

AtomSurf : Surface Representation for Learning on Protein Structures

Recent advancements in Cryo-EM and protein structure prediction algorithms have made large-scale protein structures accessible, paving the way for machine learning-based functional annotations.The field of geometric deep learning focuses on creating methods working on geometric data. An essential aspect of learning from protein structures is representing these structures as a geometric object (be it a grid, graph, or surface) and applying a learning method tailored to this representation. The performance of a given approach will then depend on both the representation and its corresponding learning method. In this paper, we investigate representing proteins as $\textit{3D mesh surfaces}$ and incorporate them into an established representation benchmark. Our first finding is that despite promising preliminary results, the surface representation alone does not seem competitive with 3D grids. Building on this, we introduce a synergistic approach, combining surface representations with graph-based methods, resulting in a general framework that incorporates both representations in learning. We show that using this combination, we are able to obtain state-of-the-art results across $\textit{all tested tasks}$. Our code and data can be found online: https://github.com/Vincentx15/atom2D .

Understanding and Improving Features Learned in Deep Functional Maps

Deep functional maps have recently emerged as a successful paradigm for non-rigid 3D shape correspondence tasks. An essential step in this pipeline consists in learning feature functions that are used as constraints to solve for a functional map inside the network. However, the precise nature of the information learned and stored in these functions is not yet well understood. Specifically, a major question is whether these features can be used for any other objective, apart from their purely algebraic role in solving for functional map matrices. In this paper, we show that under some mild conditions, the features learned within deep functional map approaches can be used as point-wise descriptors and thus are directly comparable across different shapes, even without the necessity of solving for a functional map at test time. Furthermore, informed by our analysis, we propose effective modifications to the standard deep functional map pipeline, which promote structural properties of learned features, significantly improving the matching results. Finally, we demonstrate that previously unsuccessful attempts at using extrinsic architectures for deep functional map feature extraction can be remedied via simple architectural changes, which encourage the theoretical properties suggested by our analysis. We thus bridge the gap between intrinsic and extrinsic surface-based learning, suggesting the necessary and sufficient conditions for successful shape matching. Our code is available at https://github.com/pvnieo/clover.

Generalizable Local Feature Pre-training for Deformable Shape Analysis

Transfer learning is fundamental for addressing problems in settings with little training data. While several transfer learning approaches have been proposed in 3D, unfortunately, these solutions typically operate on an entire 3D object or even scene-level and thus, as we show, fail to generalize to new classes, such as deformable organic shapes. In addition, there is currently a lack of understanding of what makes pre-trained features transferable across significantly different 3D shape categories. In this paper, we make a step toward addressing these challenges. First, we analyze the link between feature locality and transferability in tasks involving deformable 3D objects, while also comparing different backbones and losses for local feature pre-training. We observe that with proper training, learned features can be useful in such tasks, but, crucially, only with an appropriate choice of the receptive field size. We then propose a differentiable method for optimizing the receptive field within 3D transfer learning. Jointly, this leads to the first learnable features that can successfully generalize to unseen classes of 3D shapes such as humans and animals. Our extensive experiments show that this approach leads to state-of-the-art results on several downstream tasks such as segmentation, shape correspondence, and classification. Our code is available at \url{https://github.com/pvnieo/vader}.

NCP: Neural Correspondence Prior for Effective Unsupervised Shape Matching

We present Neural Correspondence Prior (NCP), a new paradigm for computing correspondences between 3D shapes. Our approach is fully unsupervised and can lead to high-quality correspondences even in challenging cases such as sparse point clouds or non-isometric meshes, where current methods fail. Our first key observation is that, in line with neural priors observed in other domains, recent network architectures on 3D data, even without training, tend to produce pointwise features that induce plausible maps between rigid or non-rigid shapes. Secondly, we show that given a noisy map as input, training a feature extraction network with the input map as supervision tends to remove artifacts from the input and can act as a powerful correspondence denoising mechanism, both between individual pairs and within a collection. With these observations in hand, we propose a two-stage unsupervised paradigm for shape matching by (i) performing unsupervised training by adapting an existing approach to obtain an initial set of noisy matches, and (ii) using these matches to train a network in a supervised manner. We demonstrate that this approach significantly improves the accuracy of the maps, especially when trained within a collection. We show that NCP is data-efficient, fast, and achieves state-of-the-art results on many tasks. Our code can be found online: https://github.com/pvnieo/NCP.

SRFeat: Learning Locally Accurate and Globally Consistent Non-Rigid Shape Correspondence

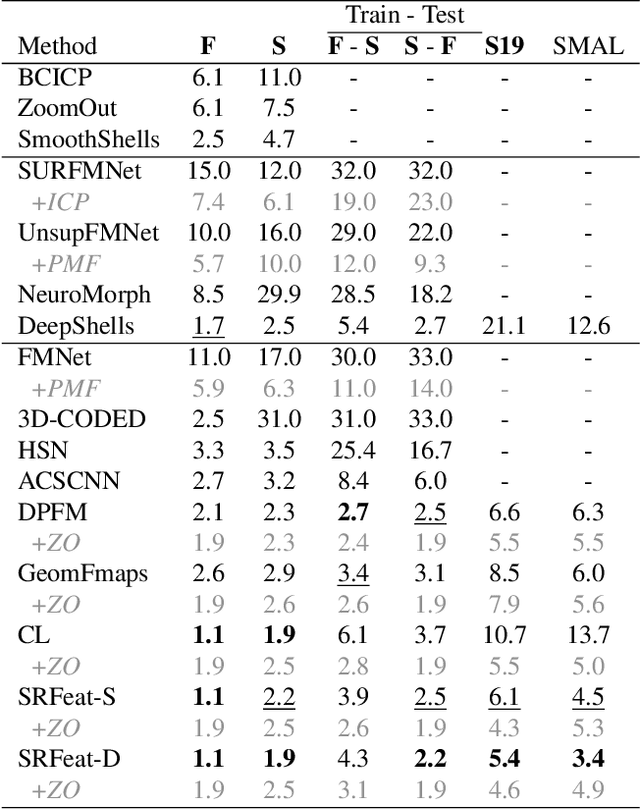
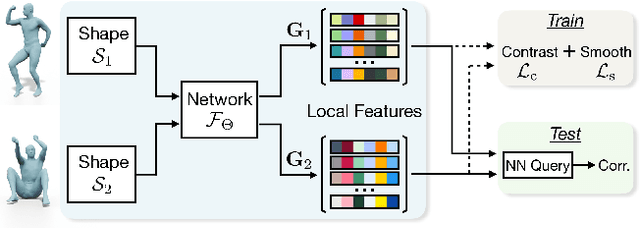
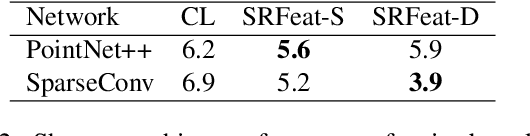
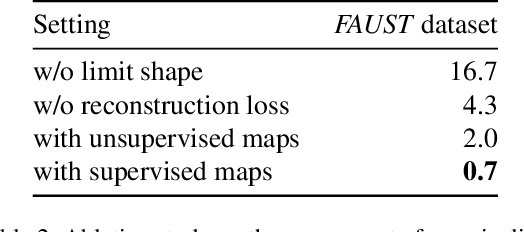
In this work, we present a novel learning-based framework that combines the local accuracy of contrastive learning with the global consistency of geometric approaches, for robust non-rigid matching. We first observe that while contrastive learning can lead to powerful point-wise features, the learned correspondences commonly lack smoothness and consistency, owing to the purely combinatorial nature of the standard contrastive losses. To overcome this limitation we propose to boost contrastive feature learning with two types of smoothness regularization that inject geometric information into correspondence learning. With this novel combination in hand, the resulting features are both highly discriminative across individual points, and, at the same time, lead to robust and consistent correspondences, through simple proximity queries. Our framework is general and is applicable to local feature learning in both the 3D and 2D domains. We demonstrate the superiority of our approach through extensive experiments on a wide range of challenging matching benchmarks, including 3D non-rigid shape correspondence and 2D image keypoint matching.

Why you should learn functional basis

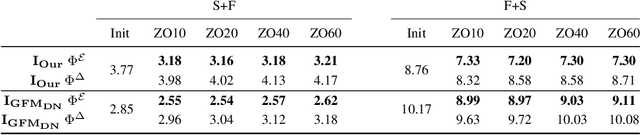
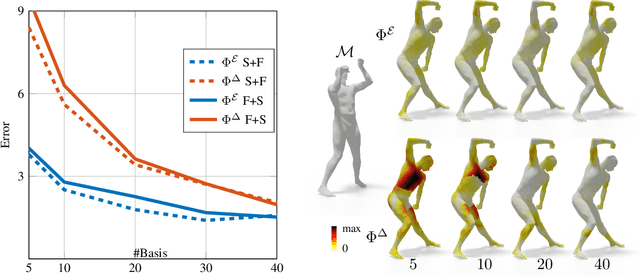
Efficient and practical representation of geometric data is a ubiquitous problem for several applications in geometry processing. A widely used choice is to encode the 3D objects through their spectral embedding, associating to each surface point the values assumed at that point by a truncated subset of the eigenfunctions of a differential operator (typically the Laplacian). Several attempts to define new, preferable embeddings for different applications have seen the light during the last decade. Still, the standard Laplacian eigenfunctions remain solidly at the top of the available solutions, despite their limitations, such as being limited to near-isometries for shape matching. Recently, a new trend shows advantages in learning substitutes for the Laplacian eigenfunctions. At the same time, many research questions remain unsolved: are the new bases better than the LBO eigenfunctions, and how do they relate to them? How do they act in the functional perspective? And how to exploit these bases in new configurations in conjunction with additional features and descriptors? In this study, we properly pose these questions to improve our understanding of this emerging research direction. We show their applicative relevance in different contexts revealing some of their insights and exciting future directions.

DPFM: Deep Partial Functional Maps

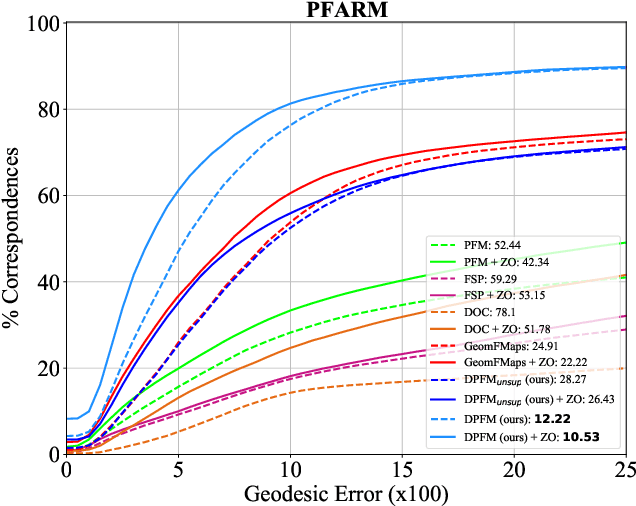
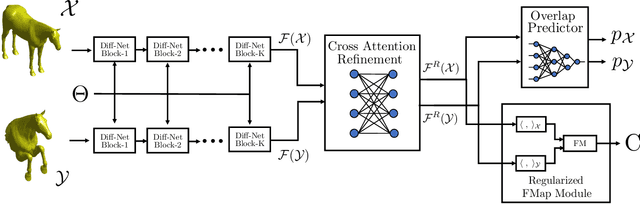
We consider the problem of computing dense correspondences between non-rigid shapes with potentially significant partiality. Existing formulations tackle this problem through heavy manifold optimization in the spectral domain, given hand-crafted shape descriptors. In this paper, we propose the first learning method aimed directly at partial non-rigid shape correspondence. Our approach uses the functional map framework, can be trained in a supervised or unsupervised manner, and learns descriptors directly from the data, thus both improving robustness and accuracy in challenging cases. Furthermore, unlike existing techniques, our method is also applicable to partial-to-partial non-rigid matching, in which the common regions on both shapes are unknown a priori. We demonstrate that the resulting method is data-efficient, and achieves state-of-the-art results on several benchmark datasets. Our code and data can be found online: https://github.com/pvnieo/DPFM

Diffusion is All You Need for Learning on Surfaces

We introduce a new approach to deep learning on 3D surfaces such as meshes or point clouds. Our key insight is that a simple learned diffusion layer can spatially share data in a principled manner, replacing operations like convolution and pooling which are complicated and expensive on surfaces. The only other ingredients in our network are a spatial gradient operation, which uses dot-products of derivatives to encode tangent-invariant filters, and a multi-layer perceptron applied independently at each point. The resulting architecture, which we call DiffusionNet, is remarkably simple, efficient, and scalable. Continuously optimizing for spatial support avoids the need to pick neighborhood sizes or filter widths a priori, or worry about their impact on network size/training time. Furthermore, the principled, geometric nature of these networks makes them agnostic to the underlying representation and insensitive to discretization. In practice, this means significant robustness to mesh sampling, and even the ability to train on a mesh and evaluate on a point cloud. Our experiments demonstrate that these networks achieve state-of-the-art results for a variety of tasks on both meshes and point clouds, including surface classification, segmentation, and non-rigid correspondence.