Deep Learning for Segmentation of Cracks in High-Resolution Images of Steel Bridges

Automating the current bridge visual inspection practices using drones and image processing techniques is a prominent way to make these inspections more effective, robust, and less expensive. In this paper, we investigate the development of a novel deep-learning method for the detection of fatigue cracks in high-resolution images of steel bridges. First, we present a novel and challenging dataset comprising of images of cracks in steel bridges. Secondly, we integrate the ConvNext neural network with a previous state-of-the-art encoder-decoder network for crack segmentation. We study and report, the effects of the use of background patches on the network performance when applied to high-resolution images of cracks in steel bridges. Finally, we introduce a loss function that allows the use of more background patches for the training process, which yields a significant reduction in false positive rates.

Optimal Transport on the Lie Group of Roto-translations

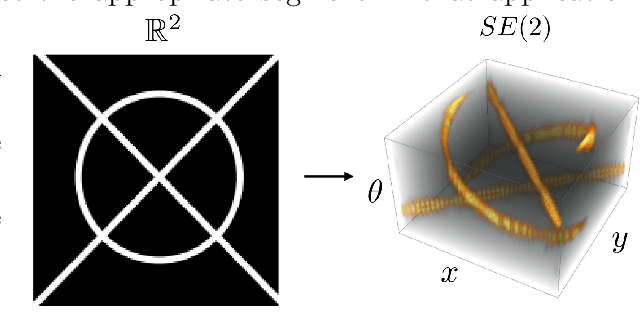
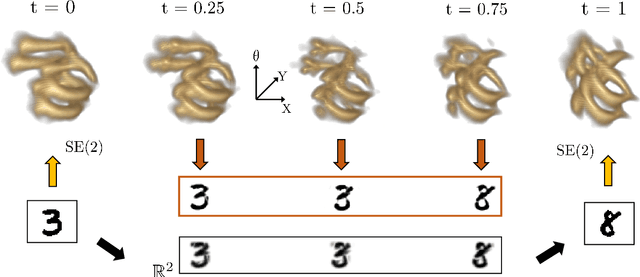
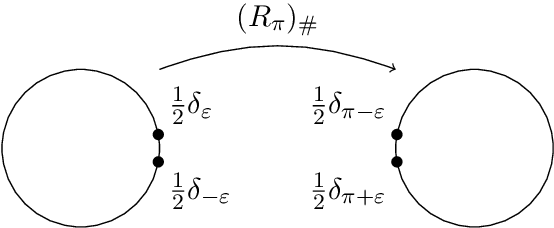
The roto-translation group SE2 has been of active interest in image analysis due to methods that lift the image data to multi-orientation representations defined on this Lie group. This has led to impactful applications of crossing-preserving flows for image de-noising, geodesic tracking, and roto-translation equivariant deep learning. In this paper, we develop a computational framework for optimal transportation over Lie groups, with a special focus on SE2. We make several theoretical contributions (generalizable to matrix Lie groups) such as the non-optimality of group actions as transport maps, invariance and equivariance of optimal transport, and the quality of the entropic-regularized optimal transport plan using geodesic distance approximations. We develop a Sinkhorn like algorithm that can be efficiently implemented using fast and accurate distance approximations of the Lie group and GPU-friendly group convolutions. We report valuable advancements in the experiments on 1) image barycentric interpolation, 2) interpolation of planar orientation fields, and 3) Wasserstein gradient flows on SE2. We observe that our framework of lifting images to SE2 and optimal transport with left-invariant anisotropic metrics leads to equivariant transport along dominant contours and salient line structures in the image. This yields sharper and more meaningful interpolations compared to their counterparts on R^2

Analysis of (sub-)Riemannian PDE-G-CNNs

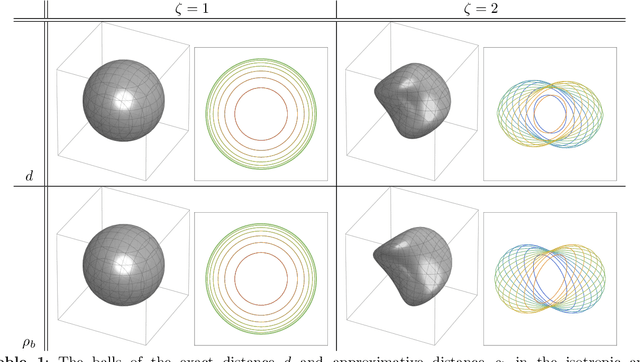
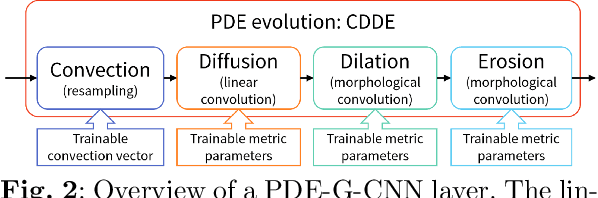
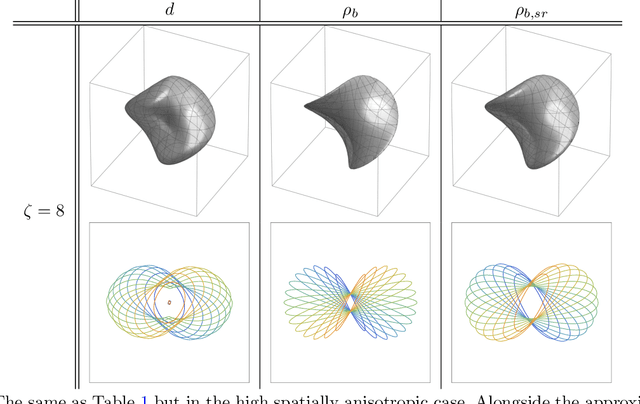
Group equivariant convolutional neural networks (G-CNNs) have been successfully applied in geometric deep-learning. Typically, G-CNNs have the advantage over CNNs that they do not waste network capacity on training symmetries that should have been hard-coded in the network. The recently introduced framework of PDE-based G-CNNs (PDE-G-CNNs) generalize G-CNNs. PDE-G-CNNs have the core advantages that they simultaneously 1) reduce network complexity, 2) increase classification performance, 3) provide geometric network interpretability. Their implementations solely consist of linear and morphological convolutions with kernels. In this paper we show that the previously suggested approximative morphological kernels do not always approximate the exact kernels accurately. More specifically, depending on the spatial anisotropy of the Riemannian metric, we argue that one must resort to sub-Riemannian approximations. We solve this problem by providing a new approximative kernel that works regardless of the anisotropy. We provide new theorems with better error estimates of the approximative kernels, and prove that they all carry the same reflectional symmetries as the exact ones. We test the effectiveness of multiple approximative kernels within the PDE-G-CNN framework on two datasets, and observe an improvement with the new approximative kernel. We report that the PDE-G-CNNs again allow for a considerable reduction of network complexity while having a comparable or better performance than G-CNNs and CNNs on the two datasets. Moreover, PDE-G-CNNs have the advantage of better geometric interpretability over G-CNNs, as the morphological kernels are related to association fields from neurogeometry.

Implicit field supervision for robust non-rigid shape matching

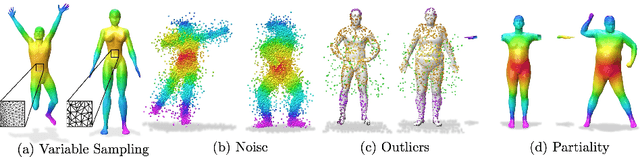
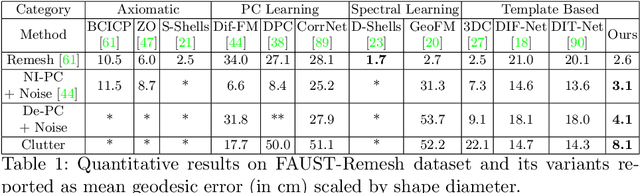
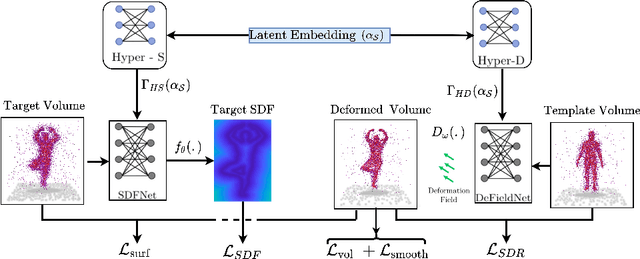
Establishing a correspondence between two non-rigidly deforming shapes is one of the most fundamental problems in visual computing. Existing methods often show weak resilience when presented with challenges innate to real-world data such as noise, outliers, self-occlusion etc. On the other hand, auto-decoders have demonstrated strong expressive power in learning geometrically meaningful latent embeddings. However, their use in shape analysis and especially in non-rigid shape correspondence has been limited. In this paper, we introduce an approach based on auto-decoder framework, that learns a continuous shape-wise deformation field over a fixed template. By supervising the deformation field for points on-surface and regularising for points off-surface through a novel Signed Distance Regularisation (SDR), we learn an alignment between the template and shape volumes. Unlike classical correspondence techniques, our method is remarkably robust in the presence of strong artefacts and can be generalised to arbitrary shape categories. Trained on clean water-tight meshes, without any data-augmentation, we demonstrate compelling performance on compromised data and real-world scans.

DPFM: Deep Partial Functional Maps

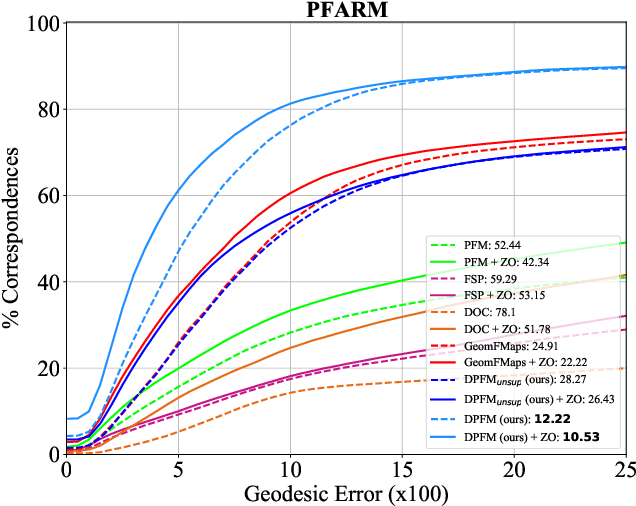
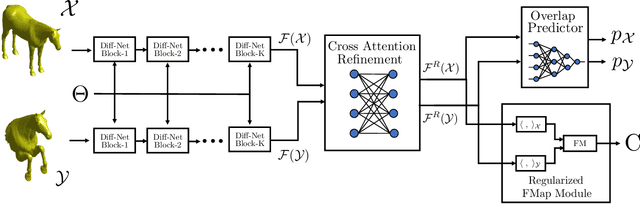
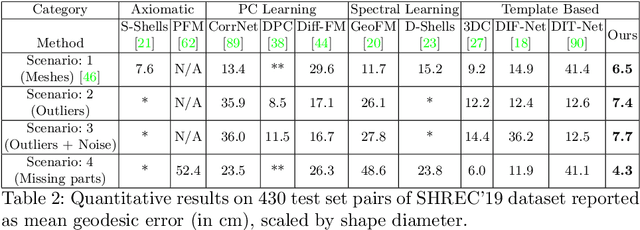
We consider the problem of computing dense correspondences between non-rigid shapes with potentially significant partiality. Existing formulations tackle this problem through heavy manifold optimization in the spectral domain, given hand-crafted shape descriptors. In this paper, we propose the first learning method aimed directly at partial non-rigid shape correspondence. Our approach uses the functional map framework, can be trained in a supervised or unsupervised manner, and learns descriptors directly from the data, thus both improving robustness and accuracy in challenging cases. Furthermore, unlike existing techniques, our method is also applicable to partial-to-partial non-rigid matching, in which the common regions on both shapes are unknown a priori. We demonstrate that the resulting method is data-efficient, and achieves state-of-the-art results on several benchmark datasets. Our code and data can be found online: https://github.com/pvnieo/DPFM

Bilateral Operators for Functional Maps

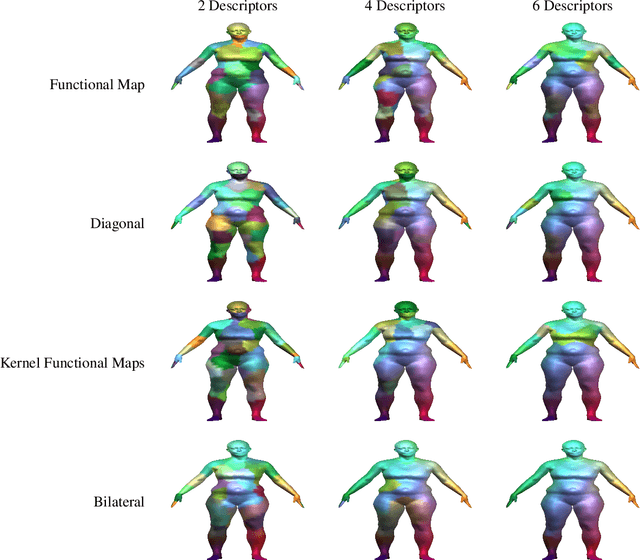
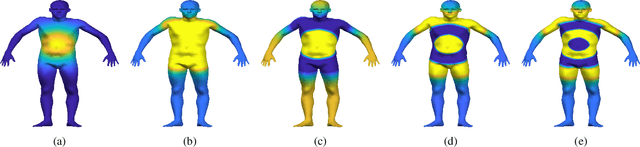
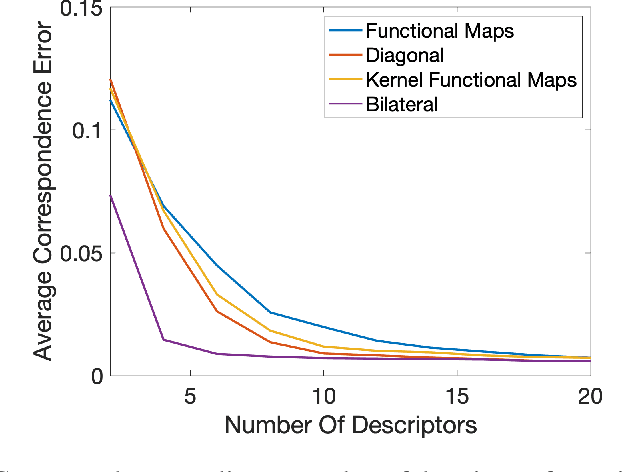
A majority of shape correspondence frameworks are based on devising pointwise and pairwise constraints on the correspondence map. The functional maps framework allows for formulating these constraints in the spectral domain. In this paper, we develop a functional map framework for the shape correspondence problem by constructing pairwise constraints using point-wise descriptors. Our core observation is that, every point-wise descriptor allows for the construction a pairwise kernel operator whose low frequency eigenfunctions depict regions of similar descriptor values at various scales of frequency. By aggregating the pairwise information from the descriptor and the intrinsic geometry of the surface encoded in the heat kernel, we construct a hybrid kernel and call it the bilateral operator. Analogous to the edge preserving bilateral filter in image processing, the action of the bilateral operator on a function defined over the manifold yields a descriptor dependent local smoothing of that function. By forcing the correspondence map to commute with the Bilateral operator, we show that we can maximally exploit the information from a given set of pointwise descriptors in a functional map framework.

Deep Eikonal Solvers

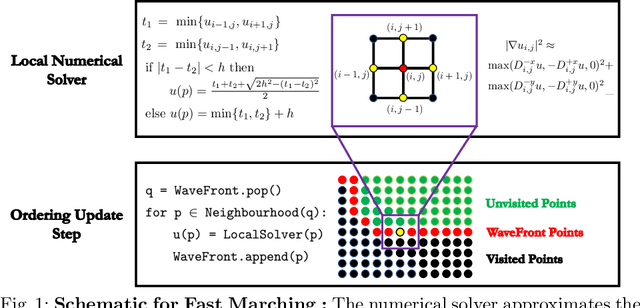
A deep learning approach to numerically approximate the solution to the Eikonal equation is introduced. The proposed method is built on the fast marching scheme which comprises of two components: a local numerical solver and an update scheme. We replace the formulaic local numerical solver with a trained neural network to provide highly accurate estimates of local distances for a variety of different geometries and sampling conditions. Our learning approach generalizes not only to flat Euclidean domains but also to curved surfaces enabled by the incorporation of certain invariant features in the neural network architecture. We show a considerable gain in performance, validated by smaller errors and higher orders of accuracy for the numerical solutions of the Eikonal equation computed on different surfaces The proposed approach leverages the approximation power of neural networks to enhance the performance of numerical algorithms, thereby, connecting the somewhat disparate themes of numerical geometry and learning.

Sparse Approximation of 3D Meshes using the Spectral Geometry of the Hamiltonian Operator

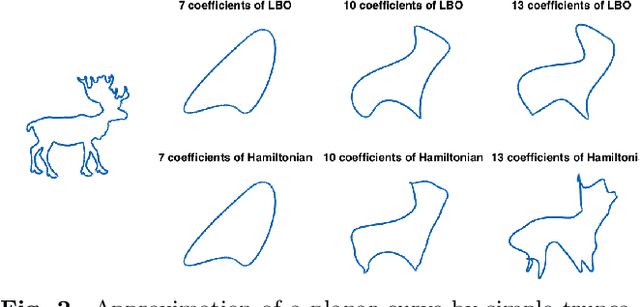
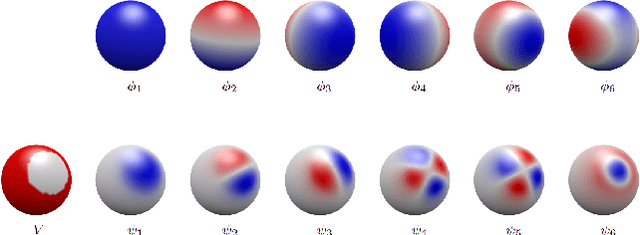
The discrete Laplace operator is ubiquitous in spectral shape analysis, since its eigenfunctions are provably optimal in representing smooth functions defined on the surface of the shape. Indeed, subspaces defined by its eigenfunctions have been utilized for shape compression, treating the coordinates as smooth functions defined on the given surface. However, surfaces of shapes in nature often contain geometric structures for which the general smoothness assumption may fail to hold. At the other end, some explicit mesh compression algorithms utilize the order by which vertices that represent the surface are traversed, a property which has been ignored in spectral approaches. Here, we incorporate the order of vertices into an operator that defines a novel spectral domain. We propose a method for representing 3D meshes using the spectral geometry of the Hamiltonian operator, integrated within a sparse approximation framework. We adapt the concept of a potential function from quantum physics and incorporate vertex ordering information into the potential, yielding a novel data-dependent operator. The potential function modifies the spectral geometry of the Laplacian to focus on regions with finer details of the given surface. By sparsely encoding the geometry of the shape using the proposed data-dependent basis, we improve compression performance compared to previous results that use the standard Laplacian basis and spectral graph wavelets.

Parametric Manifold Learning Via Sparse Multidimensional Scaling

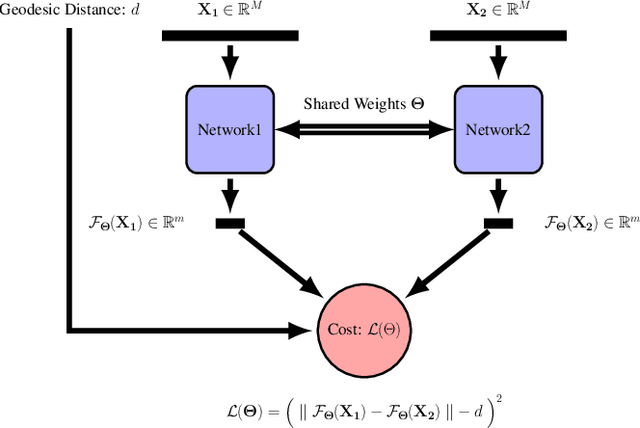
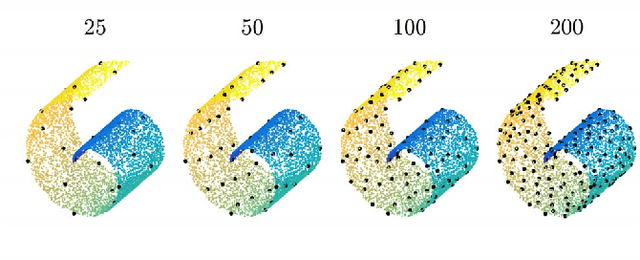
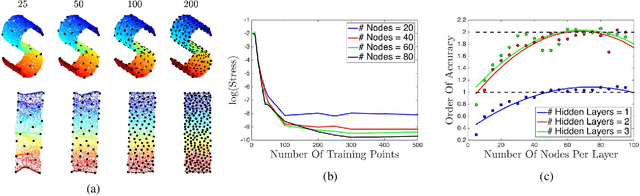
We propose a metric-learning framework for computing distance-preserving maps that generate low-dimensional embeddings for a certain class of manifolds. We employ Siamese networks to solve the problem of least squares multidimensional scaling for generating mappings that preserve geodesic distances on the manifold. In contrast to previous parametric manifold learning methods we show a substantial reduction in training effort enabled by the computation of geodesic distances in a farthest point sampling strategy. Additionally, the use of a network to model the distance-preserving map reduces the complexity of the multidimensional scaling problem and leads to an improved non-local generalization of the manifold compared to analogous non-parametric counterparts. We demonstrate our claims on point-cloud data and on image manifolds and show a numerical analysis of our technique to facilitate a greater understanding of the representational power of neural networks in modeling manifold data.

Learning Invariant Representations Of Planar Curves

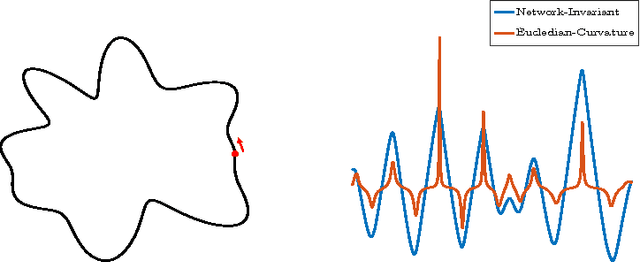
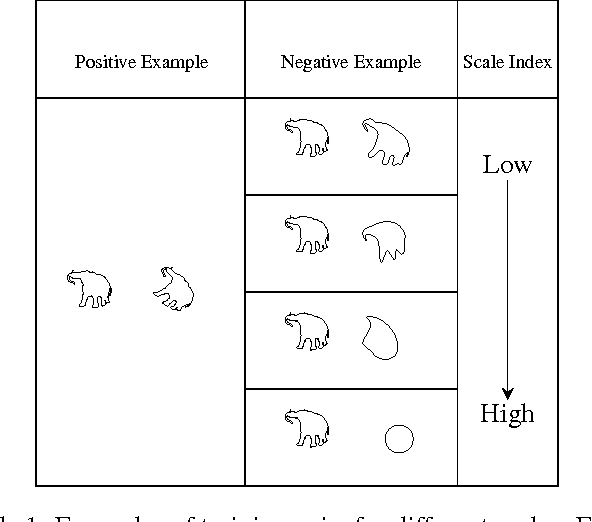
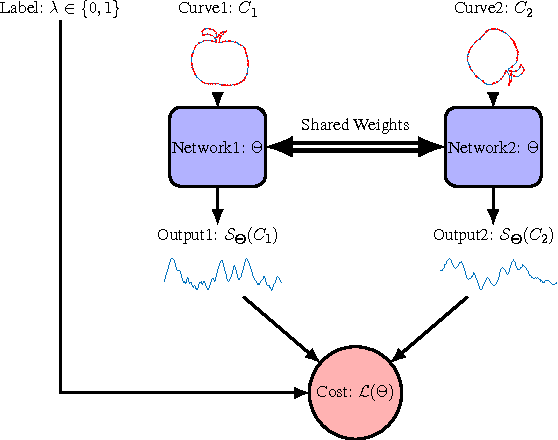
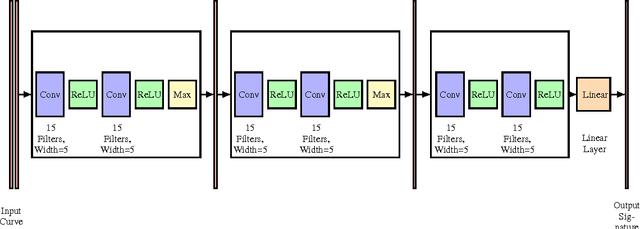
We propose a metric learning framework for the construction of invariant geometric functions of planar curves for the Eucledian and Similarity group of transformations. We leverage on the representational power of convolutional neural networks to compute these geometric quantities. In comparison with axiomatic constructions, we show that the invariants approximated by the learning architectures have better numerical qualities such as robustness to noise, resiliency to sampling, as well as the ability to adapt to occlusion and partiality. Finally, we develop a novel multi-scale representation in a similarity metric learning paradigm.