Daan Bon
Optimal Transport on the Lie Group of Roto-translations
Mar 05, 2024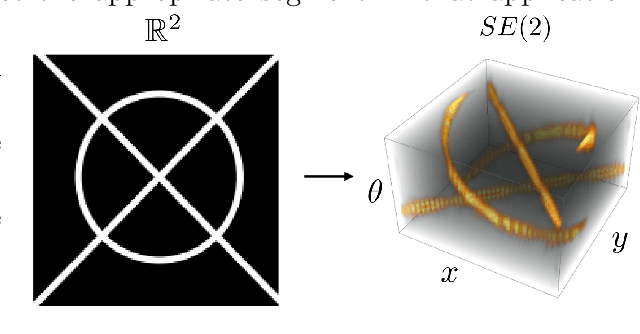
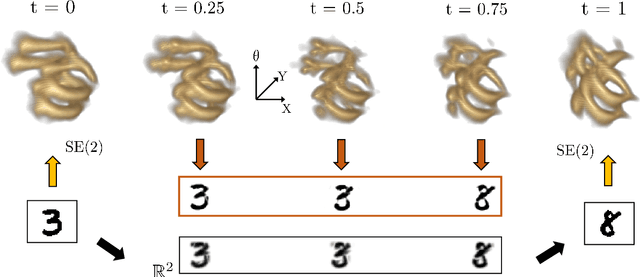

Abstract:The roto-translation group SE2 has been of active interest in image analysis due to methods that lift the image data to multi-orientation representations defined on this Lie group. This has led to impactful applications of crossing-preserving flows for image de-noising, geodesic tracking, and roto-translation equivariant deep learning. In this paper, we develop a computational framework for optimal transportation over Lie groups, with a special focus on SE2. We make several theoretical contributions (generalizable to matrix Lie groups) such as the non-optimality of group actions as transport maps, invariance and equivariance of optimal transport, and the quality of the entropic-regularized optimal transport plan using geodesic distance approximations. We develop a Sinkhorn like algorithm that can be efficiently implemented using fast and accurate distance approximations of the Lie group and GPU-friendly group convolutions. We report valuable advancements in the experiments on 1) image barycentric interpolation, 2) interpolation of planar orientation fields, and 3) Wasserstein gradient flows on SE2. We observe that our framework of lifting images to SE2 and optimal transport with left-invariant anisotropic metrics leads to equivariant transport along dominant contours and salient line structures in the image. This yields sharper and more meaningful interpolations compared to their counterparts on R^2
Analysis of (sub-)Riemannian PDE-G-CNNs
Oct 03, 2022
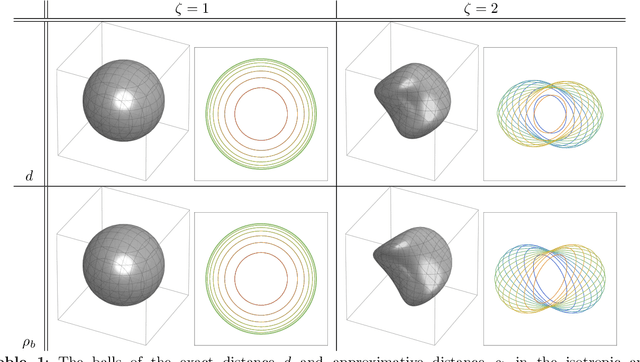
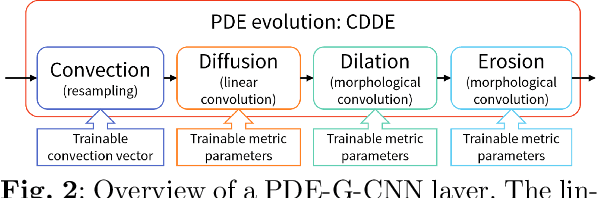
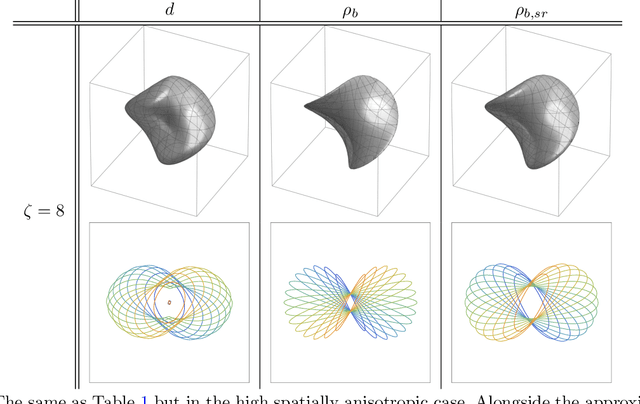
Abstract:Group equivariant convolutional neural networks (G-CNNs) have been successfully applied in geometric deep-learning. Typically, G-CNNs have the advantage over CNNs that they do not waste network capacity on training symmetries that should have been hard-coded in the network. The recently introduced framework of PDE-based G-CNNs (PDE-G-CNNs) generalize G-CNNs. PDE-G-CNNs have the core advantages that they simultaneously 1) reduce network complexity, 2) increase classification performance, 3) provide geometric network interpretability. Their implementations solely consist of linear and morphological convolutions with kernels. In this paper we show that the previously suggested approximative morphological kernels do not always approximate the exact kernels accurately. More specifically, depending on the spatial anisotropy of the Riemannian metric, we argue that one must resort to sub-Riemannian approximations. We solve this problem by providing a new approximative kernel that works regardless of the anisotropy. We provide new theorems with better error estimates of the approximative kernels, and prove that they all carry the same reflectional symmetries as the exact ones. We test the effectiveness of multiple approximative kernels within the PDE-G-CNN framework on two datasets, and observe an improvement with the new approximative kernel. We report that the PDE-G-CNNs again allow for a considerable reduction of network complexity while having a comparable or better performance than G-CNNs and CNNs on the two datasets. Moreover, PDE-G-CNNs have the advantage of better geometric interpretability over G-CNNs, as the morphological kernels are related to association fields from neurogeometry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge