Remco Duits
Bert
Equivariant Eikonal Neural Networks: Grid-Free, Scalable Travel-Time Prediction on Homogeneous Spaces
May 21, 2025Abstract:We introduce Equivariant Neural Eikonal Solvers, a novel framework that integrates Equivariant Neural Fields (ENFs) with Neural Eikonal Solvers. Our approach employs a single neural field where a unified shared backbone is conditioned on signal-specific latent variables - represented as point clouds in a Lie group - to model diverse Eikonal solutions. The ENF integration ensures equivariant mapping from these latent representations to the solution field, delivering three key benefits: enhanced representation efficiency through weight-sharing, robust geometric grounding, and solution steerability. This steerability allows transformations applied to the latent point cloud to induce predictable, geometrically meaningful modifications in the resulting Eikonal solution. By coupling these steerable representations with Physics-Informed Neural Networks (PINNs), our framework accurately models Eikonal travel-time solutions while generalizing to arbitrary Riemannian manifolds with regular group actions. This includes homogeneous spaces such as Euclidean, position-orientation, spherical, and hyperbolic manifolds. We validate our approach through applications in seismic travel-time modeling of 2D and 3D benchmark datasets. Experimental results demonstrate superior performance, scalability, adaptability, and user controllability compared to existing Neural Operator-based Eikonal solver methods.
Universal Collection of Euclidean Invariants between Pairs of Position-Orientations
Apr 04, 2025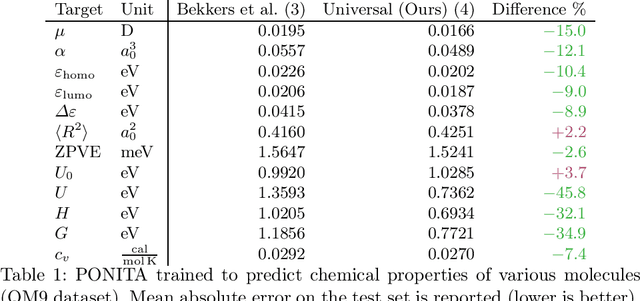
Abstract:Euclidean E(3) equivariant neural networks that employ scalar fields on position-orientation space M(3) have been effectively applied to tasks such as predicting molecular dynamics and properties. To perform equivariant convolutional-like operations in these architectures one needs Euclidean invariant kernels on M(3) x M(3). In practice, a handcrafted collection of invariants is selected, and this collection is then fed into multilayer perceptrons to parametrize the kernels. We rigorously describe an optimal collection of 4 smooth scalar invariants on the whole of M(3) x M(3). With optimal we mean that the collection is independent and universal, meaning that all invariants are pertinent, and any invariant kernel is a function of them. We evaluate two collections of invariants, one universal and one not, using the PONITA neural network architecture. Our experiments show that using a collection of invariants that is universal positively impacts the accuracy of PONITA significantly.
Orientation Scores should be a Piece of Cake
Apr 01, 2025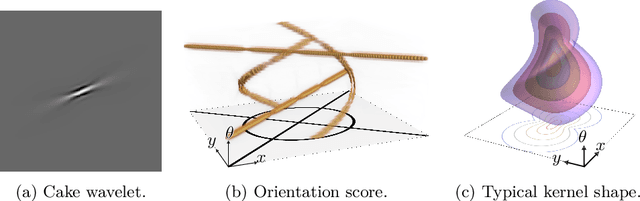
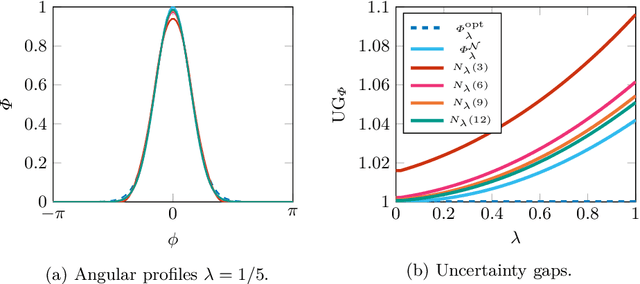
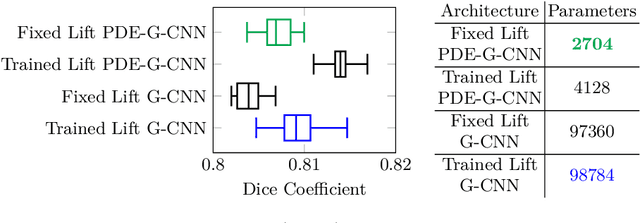
Abstract:We axiomatically derive a family of wavelets for an orientation score, lifting from position space $\mathbb{R}^2$ to position and orientation space $\mathbb{R}^2\times S^1$, with fast reconstruction property, that minimise position-orientation uncertainty. We subsequently show that these minimum uncertainty states are well-approximated by cake wavelets: for standard parameters, the uncertainty gap of cake wavelets is less than 1.1, and in the limit, we prove the uncertainty gap tends to the minimum of 1. Next, we complete a previous theoretical argument that one does not have to train the lifting layer in (PDE-)G-CNNs, but can instead use cake wavelets. Finally, we show experimentally that in this way we can reduce the network complexity and improve the interpretability of (PDE-)G-CNNs, with only a slight impact on the model's performance.
Semiring Activation in Neural Networks
May 29, 2024Abstract:We introduce a class of trainable nonlinear operators based on semirings that are suitable for use in neural networks. These operators generalize the traditional alternation of linear operators with activation functions in neural networks. Semirings are algebraic structures that describe a generalised notation of linearity, greatly expanding the range of trainable operators that can be included in neural networks. In fact, max- or min-pooling operations are convolutions in the tropical semiring with a fixed kernel. We perform experiments where we replace the activation functions for trainable semiring-based operators to show that these are viable operations to include in fully connected as well as convolutional neural networks (ConvNeXt). We discuss some of the challenges of replacing traditional activation functions with trainable semiring activations and the trade-offs of doing so.
Segmentation tool for images of cracks
Mar 28, 2024Abstract:Safety-critical infrastructures, such as bridges, are periodically inspected to check for existing damage, such as fatigue cracks and corrosion, and to guarantee the safe use of the infrastructure. Visual inspection is the most frequent type of general inspection, despite the fact that its detection capability is rather limited, especially for fatigue cracks. Machine learning algorithms can be used for augmenting the capability of classical visual inspection of bridge structures, however, the implementation of such an algorithm requires a massive annotated training dataset, which is time-consuming to produce. This paper proposes a semi-automatic crack segmentation tool that eases the manual segmentation of cracks on images needed to create a training dataset for a machine learning algorithm. Also, it can be used to measure the geometry of the crack. This tool makes use of an image processing algorithm, which was initially developed for the analysis of vascular systems on retinal images. The algorithm relies on a multi-orientation wavelet transform, which is applied to the image to construct the so-called "orientation scores", i.e. a modified version of the image. Afterwards, the filtered orientation scores are used to formulate an optimal path problem that identifies the crack. The globally optimal path between manually selected crack endpoints is computed, using a state-of-the-art geometric tracking method. The pixel-wise segmentation is done afterwards using the obtained crack path. The proposed method outperforms fully automatic methods and shows potential to be an adequate alternative to the manual data annotation.
Deep Learning for Segmentation of Cracks in High-Resolution Images of Steel Bridges
Mar 26, 2024



Abstract:Automating the current bridge visual inspection practices using drones and image processing techniques is a prominent way to make these inspections more effective, robust, and less expensive. In this paper, we investigate the development of a novel deep-learning method for the detection of fatigue cracks in high-resolution images of steel bridges. First, we present a novel and challenging dataset comprising of images of cracks in steel bridges. Secondly, we integrate the ConvNext neural network with a previous state-of-the-art encoder-decoder network for crack segmentation. We study and report, the effects of the use of background patches on the network performance when applied to high-resolution images of cracks in steel bridges. Finally, we introduce a loss function that allows the use of more background patches for the training process, which yields a significant reduction in false positive rates.
PDE-CNNs: Axiomatic Derivations and Applications
Mar 22, 2024Abstract:PDE-based Group Convolutional Neural Networks (PDE-G-CNNs) utilize solvers of geometrically meaningful evolution PDEs as substitutes for the conventional components in G-CNNs. PDE-G-CNNs offer several key benefits all at once: fewer parameters, inherent equivariance, better performance, data efficiency, and geometric interpretability. In this article we focus on Euclidean equivariant PDE-G-CNNs where the feature maps are two dimensional throughout. We call this variant of the framework a PDE-CNN. We list several practically desirable axioms and derive from these which PDEs should be used in a PDE-CNN. Here our approach to geometric learning via PDEs is inspired by the axioms of classical linear and morphological scale-space theory, which we generalize by introducing semifield-valued signals. Furthermore, we experimentally confirm for small networks that PDE-CNNs offer fewer parameters, better performance, and data efficiency in comparison to CNNs. We also investigate what effect the use of different semifields has on the performance of the models.
Optimal Transport on the Lie Group of Roto-translations
Mar 05, 2024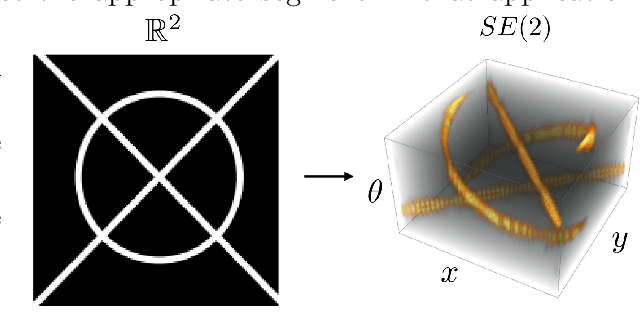
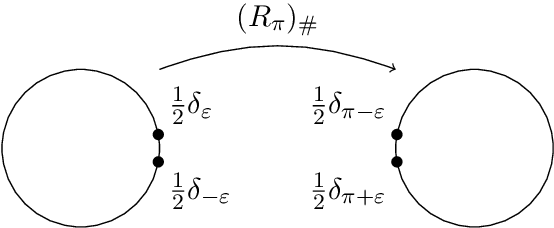

Abstract:The roto-translation group SE2 has been of active interest in image analysis due to methods that lift the image data to multi-orientation representations defined on this Lie group. This has led to impactful applications of crossing-preserving flows for image de-noising, geodesic tracking, and roto-translation equivariant deep learning. In this paper, we develop a computational framework for optimal transportation over Lie groups, with a special focus on SE2. We make several theoretical contributions (generalizable to matrix Lie groups) such as the non-optimality of group actions as transport maps, invariance and equivariance of optimal transport, and the quality of the entropic-regularized optimal transport plan using geodesic distance approximations. We develop a Sinkhorn like algorithm that can be efficiently implemented using fast and accurate distance approximations of the Lie group and GPU-friendly group convolutions. We report valuable advancements in the experiments on 1) image barycentric interpolation, 2) interpolation of planar orientation fields, and 3) Wasserstein gradient flows on SE2. We observe that our framework of lifting images to SE2 and optimal transport with left-invariant anisotropic metrics leads to equivariant transport along dominant contours and salient line structures in the image. This yields sharper and more meaningful interpolations compared to their counterparts on R^2
Analysis of (sub-)Riemannian PDE-G-CNNs
Oct 03, 2022
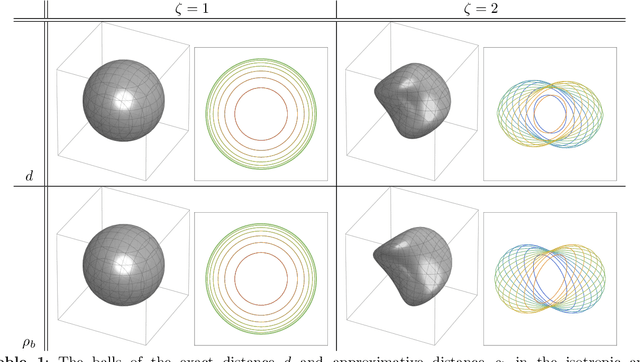
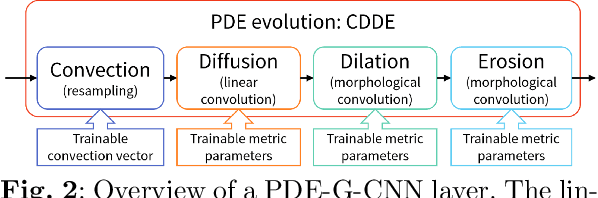
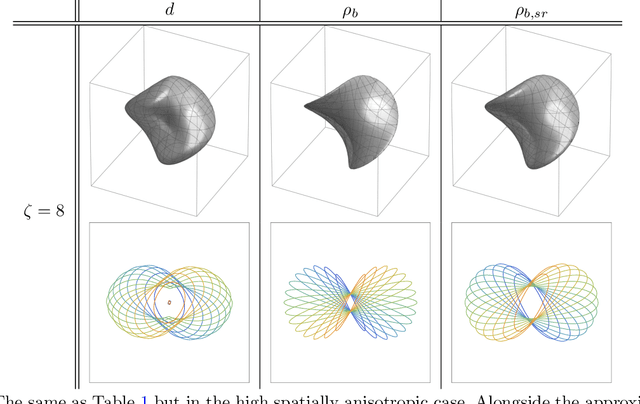
Abstract:Group equivariant convolutional neural networks (G-CNNs) have been successfully applied in geometric deep-learning. Typically, G-CNNs have the advantage over CNNs that they do not waste network capacity on training symmetries that should have been hard-coded in the network. The recently introduced framework of PDE-based G-CNNs (PDE-G-CNNs) generalize G-CNNs. PDE-G-CNNs have the core advantages that they simultaneously 1) reduce network complexity, 2) increase classification performance, 3) provide geometric network interpretability. Their implementations solely consist of linear and morphological convolutions with kernels. In this paper we show that the previously suggested approximative morphological kernels do not always approximate the exact kernels accurately. More specifically, depending on the spatial anisotropy of the Riemannian metric, we argue that one must resort to sub-Riemannian approximations. We solve this problem by providing a new approximative kernel that works regardless of the anisotropy. We provide new theorems with better error estimates of the approximative kernels, and prove that they all carry the same reflectional symmetries as the exact ones. We test the effectiveness of multiple approximative kernels within the PDE-G-CNN framework on two datasets, and observe an improvement with the new approximative kernel. We report that the PDE-G-CNNs again allow for a considerable reduction of network complexity while having a comparable or better performance than G-CNNs and CNNs on the two datasets. Moreover, PDE-G-CNNs have the advantage of better geometric interpretability over G-CNNs, as the morphological kernels are related to association fields from neurogeometry.
Roto-Translation Equivariant Convolutional Networks: Application to Histopathology Image Analysis
Feb 20, 2020



Abstract:Rotation-invariance is a desired property of machine-learning models for medical image analysis and in particular for computational pathology applications. We propose a framework to encode the geometric structure of the special Euclidean motion group SE(2) in convolutional networks to yield translation and rotation equivariance via the introduction of SE(2)-group convolution layers. This structure enables models to learn feature representations with a discretized orientation dimension that guarantees that their outputs are invariant under a discrete set of rotations. Conventional approaches for rotation invariance rely mostly on data augmentation, but this does not guarantee the robustness of the output when the input is rotated. At that, trained conventional CNNs may require test-time rotation augmentation to reach their full capability. This study is focused on histopathology image analysis applications for which it is desirable that the arbitrary global orientation information of the imaged tissues is not captured by the machine learning models. The proposed framework is evaluated on three different histopathology image analysis tasks (mitosis detection, nuclei segmentation and tumor classification). We present a comparative analysis for each problem and show that consistent increase of performances can be achieved when using the proposed framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge