Analysis of (sub-)Riemannian PDE-G-CNNs

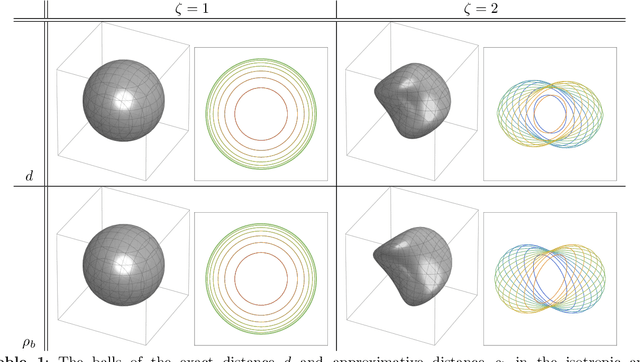
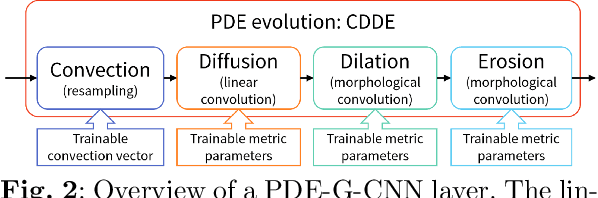
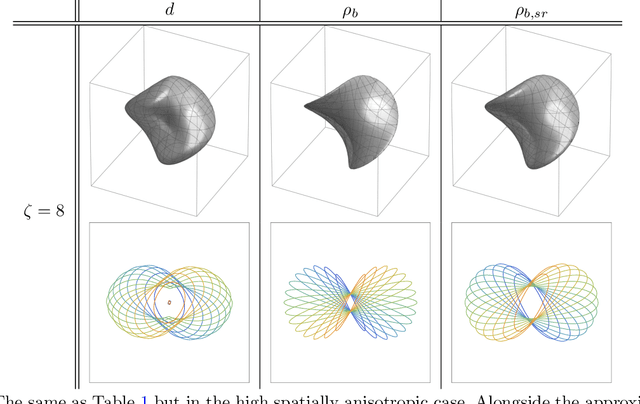
Group equivariant convolutional neural networks (G-CNNs) have been successfully applied in geometric deep-learning. Typically, G-CNNs have the advantage over CNNs that they do not waste network capacity on training symmetries that should have been hard-coded in the network. The recently introduced framework of PDE-based G-CNNs (PDE-G-CNNs) generalize G-CNNs. PDE-G-CNNs have the core advantages that they simultaneously 1) reduce network complexity, 2) increase classification performance, 3) provide geometric network interpretability. Their implementations solely consist of linear and morphological convolutions with kernels. In this paper we show that the previously suggested approximative morphological kernels do not always approximate the exact kernels accurately. More specifically, depending on the spatial anisotropy of the Riemannian metric, we argue that one must resort to sub-Riemannian approximations. We solve this problem by providing a new approximative kernel that works regardless of the anisotropy. We provide new theorems with better error estimates of the approximative kernels, and prove that they all carry the same reflectional symmetries as the exact ones. We test the effectiveness of multiple approximative kernels within the PDE-G-CNN framework on two datasets, and observe an improvement with the new approximative kernel. We report that the PDE-G-CNNs again allow for a considerable reduction of network complexity while having a comparable or better performance than G-CNNs and CNNs on the two datasets. Moreover, PDE-G-CNNs have the advantage of better geometric interpretability over G-CNNs, as the morphological kernels are related to association fields from neurogeometry.

PDE-based Group Equivariant Convolutional Neural Networks

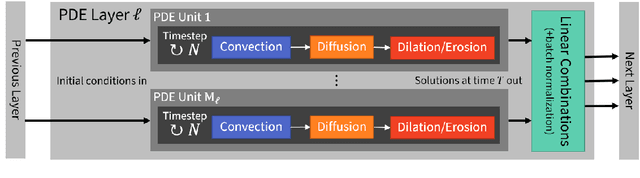
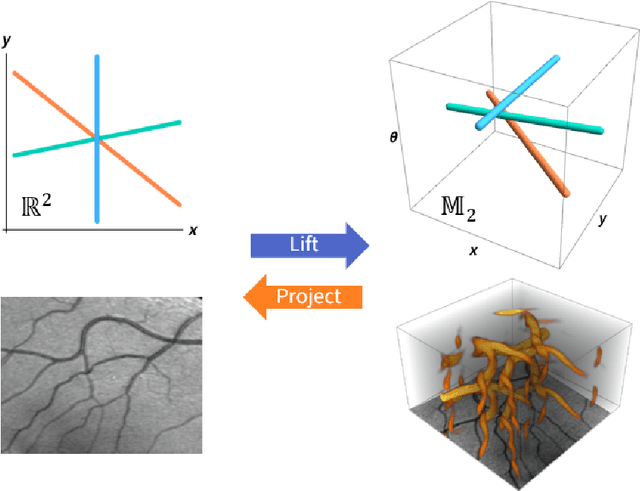
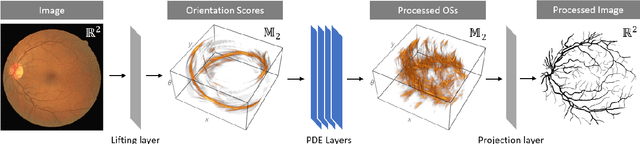
We present a PDE-based framework that generalizes Group equivariant Convolutional Neural Networks (G-CNNs). In this framework, a network layer is seen as a set of PDE-solvers where the equation's geometrically meaningful coefficients become the layer's trainable weights. Formulating our PDEs on homogeneous spaces allows these networks to be designed with built-in symmetries such as rotation equivariance instead of being restricted to just translation equivariance as in traditional CNNs. Having all the desired symmetries included in the design obviates the need to include them by means of costly techniques such as data augmentation. Roto-translation equivariance for image analysis applications is the example we will be using throughout the paper. Our default PDE is solved by a combination of linear group convolutions and non-linear morphological group convolutions. Just like for linear convolution a morphological convolution is specified by a kernel and this kernel is what is being optimized during the training process. We demonstrate how the common CNN operations of max/min-pooling and ReLUs arise naturally from solving a PDE and how they are subsumed by morphological convolutions. We present a proof-of-concept experiment to demonstrate the potential of this framework in increasing the performance of deep learning based imaging applications.