Roto-Translation Invariant Metrics on Position-Orientation Space

Riemannian metrics on the position-orientation space M(3) that are roto-translation group SE(3) invariant play a key role in image analysis tasks like enhancement, denoising, and segmentation. These metrics enable roto-translation equivariant algorithms, with the associated Riemannian distance often used in implementation. However, computing the Riemannian distance is costly, which makes it unsuitable in situations where constant recomputation is needed. We propose the mav (minimal angular velocity) distance, defined as the Riemannian length of a geometrically meaningful curve, as a practical alternative. We see an application of the mav distance in geometric deep learning. Namely, neural networks architectures such as PONITA, relies on geometric invariants to create their roto-translation equivariant model. The mav distance offers a trainable invariant, with the parameters that determine the Riemannian metric acting as learnable weights. In this paper we: 1) classify and parametrize all SE(3) invariant metrics on M(3), 2) describes how to efficiently calculate the mav distance, and 3) investigate if including the mav distance within PONITA can positively impact its accuracy in predicting molecular properties.

Universal Collection of Euclidean Invariants between Pairs of Position-Orientations

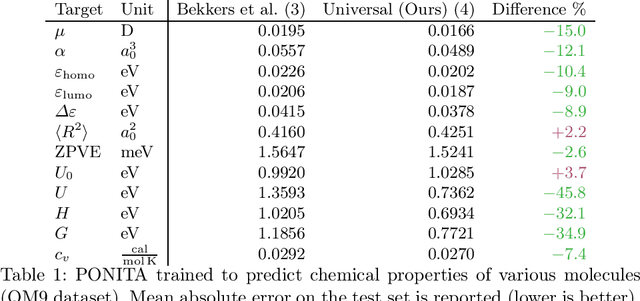
Euclidean E(3) equivariant neural networks that employ scalar fields on position-orientation space M(3) have been effectively applied to tasks such as predicting molecular dynamics and properties. To perform equivariant convolutional-like operations in these architectures one needs Euclidean invariant kernels on M(3) x M(3). In practice, a handcrafted collection of invariants is selected, and this collection is then fed into multilayer perceptrons to parametrize the kernels. We rigorously describe an optimal collection of 4 smooth scalar invariants on the whole of M(3) x M(3). With optimal we mean that the collection is independent and universal, meaning that all invariants are pertinent, and any invariant kernel is a function of them. We evaluate two collections of invariants, one universal and one not, using the PONITA neural network architecture. Our experiments show that using a collection of invariants that is universal positively impacts the accuracy of PONITA significantly.

Flow Matching on Lie Groups

Flow Matching (FM) is a recent generative modelling technique: we aim to learn how to sample from distribution $\mathfrak{X}_1$ by flowing samples from some distribution $\mathfrak{X}_0$ that is easy to sample from. The key trick is that this flow field can be trained while conditioning on the end point in $\mathfrak{X}_1$: given an end point, simply move along a straight line segment to the end point (Lipman et al. 2022). However, straight line segments are only well-defined on Euclidean space. Consequently, Chen and Lipman (2023) generalised the method to FM on Riemannian manifolds, replacing line segments with geodesics or their spectral approximations. We take an alternative point of view: we generalise to FM on Lie groups by instead substituting exponential curves for line segments. This leads to a simple, intrinsic, and fast implementation for many matrix Lie groups, since the required Lie group operations (products, inverses, exponentials, logarithms) are simply given by the corresponding matrix operations. FM on Lie groups could then be used for generative modelling with data consisting of sets of features (in $\mathbb{R}^n$) and poses (in some Lie group), e.g. the latent codes of Equivariant Neural Fields (Wessels et al. 2025).

Semiring Activation in Neural Networks

We introduce a class of trainable nonlinear operators based on semirings that are suitable for use in neural networks. These operators generalize the traditional alternation of linear operators with activation functions in neural networks. Semirings are algebraic structures that describe a generalised notation of linearity, greatly expanding the range of trainable operators that can be included in neural networks. In fact, max- or min-pooling operations are convolutions in the tropical semiring with a fixed kernel. We perform experiments where we replace the activation functions for trainable semiring-based operators to show that these are viable operations to include in fully connected as well as convolutional neural networks (ConvNeXt). We discuss some of the challenges of replacing traditional activation functions with trainable semiring activations and the trade-offs of doing so.

PDE-CNNs: Axiomatic Derivations and Applications

PDE-based Group Convolutional Neural Networks (PDE-G-CNNs) utilize solvers of geometrically meaningful evolution PDEs as substitutes for the conventional components in G-CNNs. PDE-G-CNNs offer several key benefits all at once: fewer parameters, inherent equivariance, better performance, data efficiency, and geometric interpretability. In this article we focus on Euclidean equivariant PDE-G-CNNs where the feature maps are two dimensional throughout. We call this variant of the framework a PDE-CNN. We list several practically desirable axioms and derive from these which PDEs should be used in a PDE-CNN. Here our approach to geometric learning via PDEs is inspired by the axioms of classical linear and morphological scale-space theory, which we generalize by introducing semifield-valued signals. Furthermore, we experimentally confirm for small networks that PDE-CNNs offer fewer parameters, better performance, and data efficiency in comparison to CNNs. We also investigate what effect the use of different semifields has on the performance of the models.

Mathematics of Neural Networks (Lecture Notes Graduate Course)

These are the lecture notes that accompanied the course of the same name that I taught at the Eindhoven University of Technology from 2021 to 2023. The course is intended as an introduction to neural networks for mathematics students at the graduate level and aims to make mathematics students interested in further researching neural networks. It consists of two parts: first a general introduction to deep learning that focuses on introducing the field in a formal mathematical way. The second part provides an introduction to the theory of Lie groups and homogeneous spaces and how it can be applied to design neural networks with desirable geometric equivariances. The lecture notes were made to be as self-contained as possible so as to accessible for any student with a moderate mathematics background. The course also included coding tutorials and assignments in the form of a set of Jupyter notebooks that are publicly available at https://gitlab.com/bsmetsjr/mathematics_of_neural_networks.